雷达杂波处理.ppt

雷达杂波处理.ppt

《雷达杂波处理.ppt》由会员分享，可在线阅读，更多相关《雷达杂波处理.ppt（46页珍藏版）》请在冰豆网上搜索。

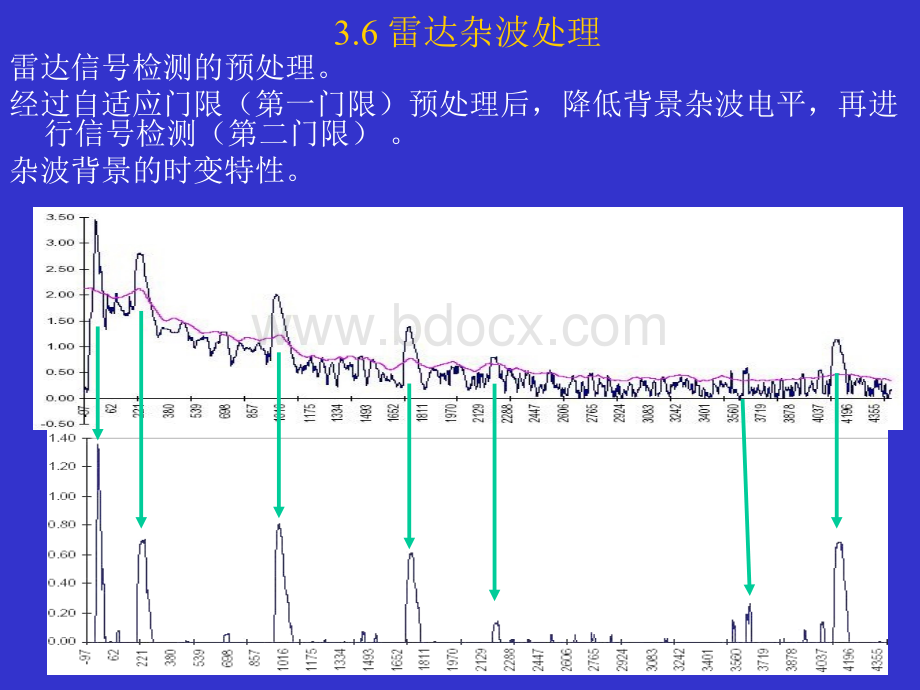
3.6雷达杂波处理雷达信号检测的预处理。

经过自适应门限（第一门限）预处理后，降低背景杂波电平，再进行信号检测（第二门限）。

杂波背景的时变特性。

3.6.1雷达杂波处理的基本任务限制虚警率基于回波信号幅度信息的统计检测采用门限检测方法，幅度大于等于门限电平，回波即为目标，幅度小于门限电平，回波即为目标。

通常，门限电平低，发现概率高，虚警也高；门限电平高，虚警率低，发现概率也低；只能兼顾发现概率和虚警概率的要求，折衷确定门限。

门限折衷确定的原则：

在系统容许的虚警率下（恒虚警率并非绝对地追求更低的虚警率），尽可能提高发现概率。

系统容许的虚警率水平的高低取决于系统处理能力（与硬件的存储容量和计算速度、目标检测方法、目标跟踪方法和系统性能要求等有关）。

虚警可通过目标检测处理（积累检测消除伪目标）和目标跟踪处理（消除伪航迹）进一步消除。

限制虚警率通常采用恒虚警率（CFAR）方法，建立自适应的检测门限。

单次检测CFAR门限随时间（距离）自适应地按杂波强度改变。

提高信噪比利用目标回波与杂波在相关性上的差异，通过相关处理提高信杂比，从根本上提高目标检测能力（在尽可能低的虚警率下获得高的发现概率）。

3.6.2雷达杂波的基本特性雷达杂波：

噪声，雨雪杂波，海杂波，同频干扰。

雷达杂波为随机量。

杂波特性（数学模型）：

统计分布特性（概率分布函数或概率分布密度函数）相关特性（相关系数）已知杂波幅度u的概率密度函数为p（u），门限电平为UT，则虚警概率为：

虚警概率为门限电平的函数。

按概率论的中心极限定理，由大量作用比较均匀的随机分量合成的随机量服从正态分布，正态分布的包络（检波后的视频信号）服从瑞利（Rayleigh）分布：

2为方差。

噪声在脉冲脉冲间统计独立，非相关。

瑞利分布特征量：

均值方差中值x=-3:

0.1:

8;y1=raylpdf（x,2）;y2=normpdf（x,2,1.4）;plot（x,y1,red,x,y2,blu）;x=0:

0.1:

10;y1=raylpdf（x,1）;y2=raylpdf（x,1.5）;y3=raylpdf（x,2）;y4=raylpdf（x,2.5）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变瑞利分布的正态分布的包络（检波后的视频信号）服从瑞利分布的证明：

按中心极限定理，ux和uy服从正态分布：

x和y为方差，ux和uy独立，且x=y=，则ux和uy的联合概率分布仍为正态分布：

22

（1）噪声的基本特性噪声服从瑞利分布，概率密度函数为：

2为方差。

噪声在脉冲脉冲间统计独立，非相关。

（2）雨雪杂波的基本特性雨雪杂波由大量散射单元形成，服从瑞利分布，概率密度函数为：

2为方差。

雨雪杂波在脉冲脉冲间具有一定的相关性。

（3）海杂波的基本特性低分辨力雷达的海杂波由大量散射单元形成，服从瑞利分布，概率密度函数为：

2为方差。

海杂波在脉冲脉冲间具有很强的相关性。

高分辨力雷达的海杂波由少量散射单元形成，服从对数正态（Log-Normal）分布和韦布尔（Weibull）分布。

对数正态概率密度函数为：

均值：

方差：

中值：

lnu符合正态分布。

与瑞利分布相比，对数正态分布出现“长尾”。

均值：

方差：

中值：

对数正态分布x=-3:

0.1:

20;y1=lognpdf（x,0.8,1）;y2=normpdf（x,2,1.4）;plot（x,y1,red,x,y2,blu）;x=0:

0.1:

6;y1=lognpdf（x,1,1）;y2=lognpdf（x,1,1.5）;y3=lognpdf（x,1,2）;y4=lognpdf（x,1,2.5）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变对数正态分布的x=0:

0.1:

30;y1=lognpdf（x,1.5,1）;y2=lognpdf（x,2,1）;y3=lognpdf（x,2.5,1）;y4=lognpdf（x,3,1）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变对数正态分布的x=0:

0.1:

12;y1=normpdf（x,4,1）;y2=normpdf（x,5,1）;y3=normpdf（x,6,1）;y4=normpdf（x,7,1）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变正态分布的x=0:

0.1:

12;y1=normpdf（x,6,1）;y2=normpdf（x,6,1.5）;y3=normpdf（x,6,2）;y4=normpdf（x,6,2.5）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变正态分布的韦布尔概率密度函数为：

均值：

方差：

中值：

为形状标度参量，为强度标度参量。

=2为瑞利分布。

x=-3:

0.1:

10;y1=wblpdf（x,3,2）;y2=normpdf（x,2,1.4）;plot（x,y1,red,x,y2,blu）;x=-3:

0.1:

10;y1=wblpdf（x,3,1.5）;y2=wblpdf（x,3,2.5）;y3=wblpdf（x,3,3.5）;y4=wblpdf（x,3,4.5）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;改变形状标度参量改变强度标度参量x=-3:

0.1:

10;y1=wblpdf（x,1,3）;y2=wblpdf（x,2,3）;y3=wblpdf（x,3,3）;y4=wblpdf（x,4,3）;plot（x,y1,red,x,y2,blu,x,y3,gre,x,y4,bla）;瑞利分布对数正态分布韦布尔分布x=0:

0.1:

6;y1=raylpdf（x,1.2）;y2=lognpdf（x,0.6,0.5）;y3=wblpdf（x,1.8,1.6）;plot（x,y1,red,x,y2,blu,x,y3,bla）;（4）同频干扰的基本特性来自确定信号的同频有源干扰（因同频雷达信号与本雷达信号无同步关系）在出现的时间（位置）上呈现随机性。

同频干扰或者出现，或者不出现，在某一时间（距离）区间内可看作是均匀分布的。

小量程大量程同频干扰的消除：

相关处理（重复频率抖动）。

2TX2X3XoX1tttt2TT0NNNSSSS自适应门限X2X3X1输出Xo输入移位寄存器移位寄存器与门判别3.6.3雷达杂波的恒虚警率处理

（1）恒虚警率处理的必要性对瑞利分布，虚警概率为的变化将引起虚警率的显著变化。

（2）瑞利杂波的恒虚警率处理根据杂波的统计分布特性实现恒虚警率处理。

以检测门限作为积分区间的起点，通过对杂波幅度的概率密度分布函数进行积分就可求出虚警（概）率。

将此过程逆过来，当要求虚警率恒定时，由概率论的方法不难得出满足恒定虚警率水平要求的积分区间的起点（检测门限电平），由此建立起来的CFAR实际上是一个门限电平取决于杂波分布参量的自适应检测器。

CFAR的关键是确定自适应的检测门限。

ConstantFalseAlarmRate对瑞利分布的杂波进行归一化处理，即令v=u将u=v代入中，得：

根据虚警率要求，对v设置门限VT=UT/，得恒虚警率：

相对u而言，门限UT=VT为与杂波参量有关的自适应门限。

如何得到的估计，以实现归一化?

，利用均值估计。

瑞利分布的均值为考虑杂波在小的距离范围内为平稳的随机过程，某点的时间均值代之以该点周围邻近区间的空间均值单元平均的CFAR。

移位寄存器串行输入并行输出，其中位于中心的S0为待检测的信号，前后两侧的2N个参考单元的样值经算术取均值运算后结果作为待检测信号所处杂波区的杂波均值估计。

恒虚警检测只是根据单次探测信号进行，并不是目标的最终检测。

在恒虚警检测的基础上，还需通过积累进行目标检测，或者说，恒虚警的自适应门限只是第一级的检测门限。

门限信号输入检测输出L移位寄存器移位寄存器S1SNSN+1S2N求均值S0门限判决单元平均CFAR的几个问题：

均值估值的稳定性参考单元数有限，均值仍为随机量，影响到虚警率的稳定性。

参考单元数多，均值估值准确稳定。

杂波边缘影响目标检测能力杂波强度估计过大，检测能力低。

参考单元参考单元参考单元参考单元目标参考单元参考单元参考单元参考单元目标杂波强度估计不足，虚警率高。

杂波的非平稳性影响虚警率的稳定性和目标的检测能力。

参考单元数越多，杂波非平稳性的影响越大，对杂波变化的敏感性越差。

参考单元中大目标的影响参考单元参考单元参考单元参考单元杂波强度估计过大，检测能力低。

（3）对数瑞利杂波的恒虚警率处理雷达接收机通常采用对数接收方式。

将uL=Aln（Bu）代入中，得uL的概率密度：

uL的均值：

式中，欧拉常数C0.557。

uL的均方值：

uL的方差：

uL的均值随u的强度2变化，uL的方差与u的强度无关，减均值可以实现恒虚警率处理。

门限信号输入检测输出L移位寄存器移位寄存器S1SNSN+1S2N求均值S0门限判决对数中放检波门限信号输入门限判决对数中放检波延时低通滤波相减器对数减均值：

（4）对数正态杂波和韦布尔杂波的恒虚警率处理对数正态杂波的CFAR对数正态杂波的概率密度分布函数令uL=lnu，得正态分布uL的概率密度：

归一化，令，v的概率密度函数为：

v的概率密度函数与u的分布参量无关，对v设置门限可实现恒虚警率。

信号输入对数放大门限检测输出S1SN门限判决平方求均值平方S1SN求均值平方EuL2EuLDuL+-v2韦布尔杂波的CFAR韦布尔概率密度函数取uL=lnu，得uL的概率密度：

uL的均值：

式中，欧拉常数C0.557，uL的均方值：

uL的方差为：

归一化，v，v的概率密度函数为：

式中，欧拉常数C0.557，p（v）与杂波参量（、）无关，亦即与杂波的均值和方差无关，因而可实现恒虚警率处理。

韦布尔杂波的归一化与对数正态杂波的归一化相同，因而杂波恒虚警率处理电路形式相同。

（5）非参量法恒虚警率处理参量法：

已知概率分布密度，需要估计未知参量。

非参量法：

采用数理统计方法，对杂波取样和信号加杂波的取样进行比较，统计地确定目标是否存在，使虚警率与杂波分布无关。

至积累检测门限L参考单元参考单元S1SNSN+1S2N被测单元门限判决CCCC当u=0，C（u）根据被比较参考信号的奇偶，交替取“0”或“1”，使C（0）等1或0的机会相同。

至积累检测门限L参考单元参考单元S1SNSN+1S2N被测单元门限判决CCCC当检测单元和参考单元只有杂波时，假定各点杂波独立同分布，则秩值大于等于L的概率（虚警概率）为11/（2N+1），回波积累数较大时才适合采用。

Rj称为秩值，表明将参考单元和被测单元按值的大小排序，按被测单元所处的位置。

该电路亦称秩值检测器。

3.6.4.雷达杂波的解相关处理3.6.4.1解相关处理的基本概念提高信噪比的依据：

目标信号与杂波在相关性上的差异性。

杂波相关性越强，通过相关处理所能得到的信噪比增益越低，杂波越难以抑制。

解（去）相关处理：

降低杂波的相关性，从而通过相关处理获得更大的信噪比增益。

利用杂波在时间、频率、极化、空间等方面的特性降低杂波的相关性。

3.6.4.2频率解相关频率相关系数i、j两个杂波间的相关系数为：

设发射波形为u（t），杂波响应为c（t），则杂波回波电压信号为：

载频为fi，宽度为的发射波形ui（t）为：

有付氏变换：

假设杂波回波是大量随机分布散射点的回波的集合，与白噪声类似，c（t）看作在时间上密集分布的（t）函数的总和，其付氏变换C（f）可认为是均匀分布的，C2（f）可用功率密度C0代替，因此：

因i、j两个不同载频发射信号的杂波回波间的频率相关系数为：

设i、j杂波回波间的频率变化表示为：

则频率相关系数为：

当f=1，=0；f1，很小；即f1/，可认为杂波不相关。

杂波频率解相关的方法：

高分辨率雷达，散射体数目少，不满足上述假设前提，但随着f的增加，频率相关系数有指数衰减的趋势，当f1/，可认为杂波不相关。

移位寄存器S1SM相关处理例：

利用相邻两次探测周期中不同频率的脉冲（频率分集）实