高中数学高考综合复习椭圆与双曲线.docx

高中数学高考综合复习椭圆与双曲线.docx

《高中数学高考综合复习椭圆与双曲线.docx》由会员分享，可在线阅读，更多相关《高中数学高考综合复习椭圆与双曲线.docx（25页珍藏版）》请在冰豆网上搜索。

高中数学高考综合复习椭圆与双曲线

高中数学高考综合复习

　　专题二十一　　椭圆与双曲线

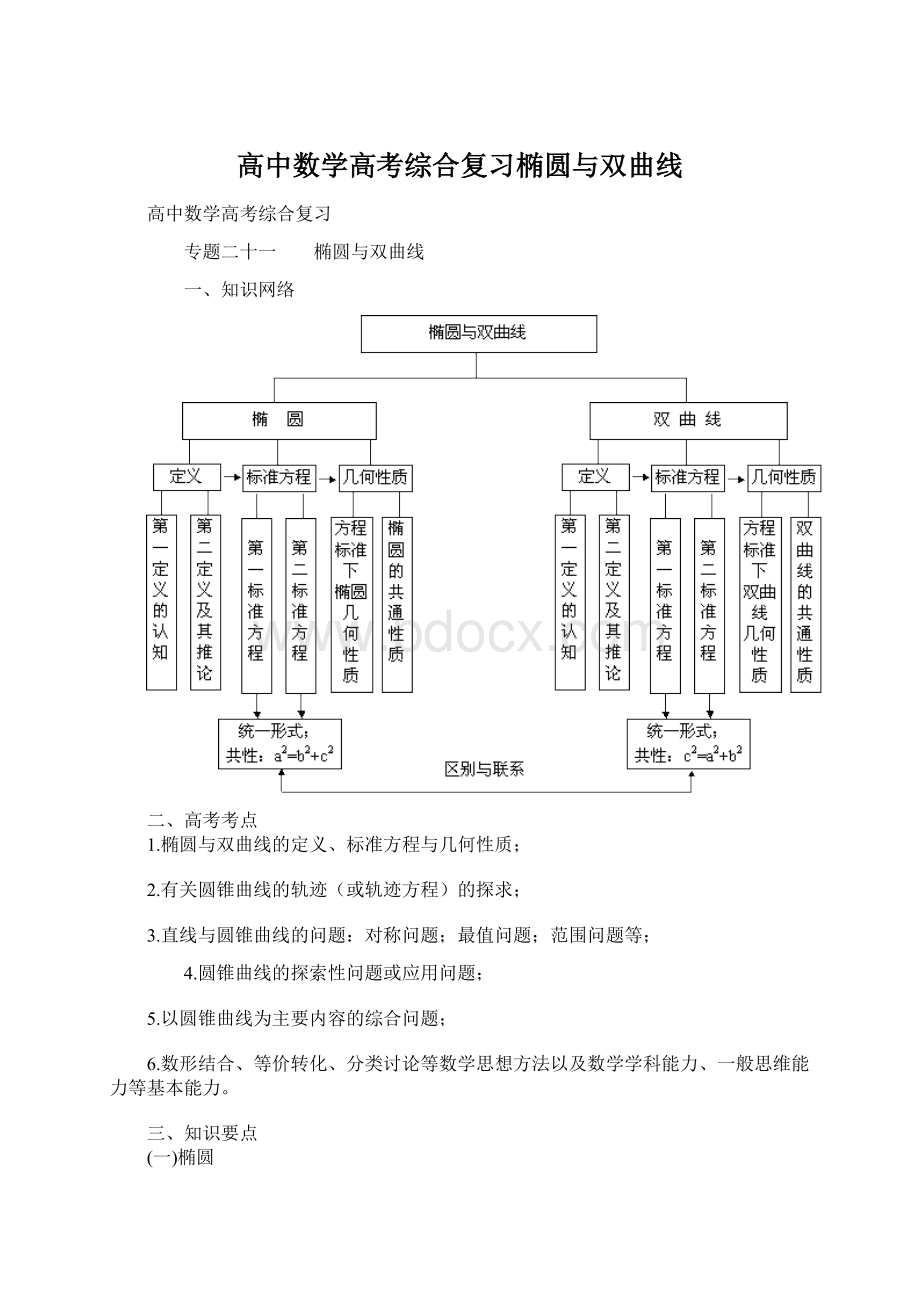
　　一、知识网络

二、高考考点

　　1.椭圆与双曲线的定义、标准方程与几何性质；

　　2.有关圆锥曲线的轨迹（或轨迹方程）的探求；

　　3.直线与圆锥曲线的问题：

对称问题；最值问题；范围问题等；

　　4.圆锥曲线的探索性问题或应用问题；

　　5.以圆锥曲线为主要内容的综合问题；

　　6.数形结合、等价转化、分类讨论等数学思想方法以及数学学科能力、一般思维能力等基本能力。

　　三、知识要点

（一）椭圆

　　Ⅰ定义与推论

　　1、定义1的的认知

　　设M为椭圆上任意一点，分别为椭圆两焦点，分别为椭圆长轴端点，则有

（1）明朗的等量关系：

（解决双焦点半径问题的首选公式）

（2）隐蔽的不等关系：

，　　

　　（寻求某些基本量取值范围时建立不等式的基本依据）

　　2、定义2的推论

　　根据椭圆第二定义，设为椭圆上任意一点，分别为椭圆左、右焦点，则有：

　　（d1为点M到左准线l1的距离）

　　（d2为点M到右准线l2的距离）

　　由此导出椭圆的焦点半径公式：

　　Ⅱ标准方程与几何性质

　　1、椭圆的标准方程

　　中心在原点，焦点在x轴上的椭圆标准方程　　①

　　中心在原点，焦点在y轴上的椭圆标准方程　　②

（1）标准方程①、②中的a、b、c具有相同的意义与相同的联系：

（2）标准方程①、②统一形式：

　　2、椭圆的几何性质

（1）范围：

（有界曲线）

（2）对称性：

关于x轴、y轴及原点对称（两轴一中心，椭圆的共性）

　　（3）顶点与轴长：

顶点，长轴2a，短轴2b（由此赋予a、b名称与几何意义）

　　（4）离心率：

刻画椭圆的扁平程度

　　（5）

　　准线：

左焦点对应的左准线

　　右焦点对应的右准线

　　椭圆共性：

两准线垂直于长轴；两准线之间的距离为；

　　中心到准线的距离为；焦点到相应准线的距离为.

　　Ⅲ挖掘与引申

　　1、具特殊联系的椭圆的方程

（1）共焦距的椭圆的方程

　　且

（2）同离心率的椭圆的方程

　　且

　　2、弦长公式：

　　设斜率为k的直线l与椭圆交于不同两点，

　　则；

　　或。

（二）双曲线

　　Ⅰ、定义与推论

　　1．定义1的认知

　　设M为双曲线上任意一点，分别为双曲线两焦点，分别为双曲线实轴端点，则有：

（1）明朗的等量关系：

（解决双焦点半径问题的首选公式）

（2）隐蔽的不等关系：

，

　　（寻求某些基本量的取值范围时建立不等式的依据）

　　2．定义2的推论

　　设为双曲线上任意上点，分别为双曲线左、右焦点，则有

　　，其中，为焦点到相应准线li的距离

　　推论：

焦点半径公式

　　当点M在双曲线右支上时，；

　　当点M在双曲线左支上时，。

　　Ⅱ、标准方程与几何性质

　　3．双曲线的标准方程

　　中心在原点，焦点在x轴上的双曲线标准方程为　　①

　　中心在原点，焦点在y轴上的双曲线标准方程为　　②

（1）标准方程①、②中的a、b、c具有相同的意义与相同的联系：

（2）标准方程①、②的统一形式：

　　或：

　　（3）椭圆与双曲线标准方程的统一形式：

　　4．双曲线的几何性质

（1）范围：

（2）对称性：

关于x轴、y轴及原点对称（两轴一中心）

　　（3）顶点与轴长：

顶点

　　（由此赋予a,b名称与几何意义）

　　（4）离心率：

　　（5）

　　准线：

左焦点对应的左准线；右焦点对应的右准线

　　双曲线共性：

准线垂直于实轴；两准线间距离为；

　　中心到准线的距离为；焦点到相应准线的距离为

　　（6）渐近线：

双曲线的渐近线方程：

　　Ⅲ、挖掘与延伸

　　1．具有特殊联系的双曲线的方程

　　对于双曲线（※）

（1）当λ+μ为定值时，（※）为共焦点的双曲线（系）方程：

c2=λ+μ;

（2）当为定值时，（※）为共离心率亦为共淅近线的双曲线（系）方程：

；

　　（3）以直线为渐近线的双曲线（系）方程为：

　　特别：

与双曲线共渐近线的双曲线的方程为：

（左边相同，区别仅在于右边的常数）

　　2．弦长公式

　　设斜率为k的直线l与双曲线交于不同两点

　　则

　　经典例题

　　1、

（1）若椭圆a2x2-y2=1的一个焦点是（-2，0），则a等于　　　　　　　　　　　　。

（2）已知椭圆的焦点为F1、F2，点P是其上的动点，当为钝角时，点P的横坐标的取值范围为　　　　　　　　　　　　　　。

　　分析：

（1）从此椭圆的标准方程切入。

　　由题设知已知得：

　　这里

　　由此解得

（2）这里a=3,b=2,c=

　　∴以线段F1F2为直径的圆的方程为

　　设，则由点P在椭圆上得：

　　　　①

　　又由为钝角得：

　　∴　　　　　　②

　　∴由①、②联立，解得：

　　∴所求点P横坐标的取值范围为

　　点评：

注意到点P对的大小的影响可用点P与圆相对位置关系来反映，故选择这一解法。

当然，本题亦可由推出的范围，请同学们尝试和比较。

　　2、已知为椭圆的两个焦点，过的直线交椭圆于P、Q两点，且，求椭圆的离心率。

　　分析：

不防设椭圆方程为，为等腰直角三角形，注意到这一三角形含有点P、Q处的两条焦点半径，故想到利用椭圆第一定义构建有关方程。

　　解：

设椭圆方程为

　　设，则由为等腰得：

　　又由椭圆第一定义得

　　∴的周长为4a

　　∴　　

　　即　　　　　　　　　　　　①

　　注意到为，

　　∴

　　∴　　　　　　　　　　　　②

　　即　　　　　　　　　　　　②′

　　因此，①代入②′得　　

　　由此解得

　　∴

　　点评：

这里对条件运用颇为充分：

两次运用椭圆定义，第一次用于导出①，第二项用于导出②；两次运用条件：

第一次利用为等腰表示出，第二次利用为导出②′。

充分利用题设条件，也是解题成功的保障之一。

　　3、已知双曲线的左、右两个焦点为，P为双曲线上的点，又，成等比数列且，求双曲线方程。

　　分析：

这里要求b的值。

注意到，为了求b，首先需要从题设条件入手寻找关于b的方程或不等式。

由题设得，为便于将其设为关于b的方程，考虑推导并利用双曲线的焦点半径公式。

因此，解题便以判定点P位置拉开序幕。

　　解：

这里（4的特殊性）

　　∵，即，

　　∴点P在双曲线右支上

　　设点，则由双曲线第二定义以及点P在双曲线右支上得

　　　　　　　　　　　　　　　　①

　　又由题设得　　　　　　②

　　∴①代入②得　　③

　　再注意到由得

　　∴，　　

　　∴　　　　　　

　　即　　　　　　　　　　　　　　　　④

　　于是③、④得　　　　⑤

　　而，所以由⑤得b=1

　　因此，所求双曲线方程为：

　　点评：

这里对已知条件的两次运用：

第一次“粗”用，利用4=2a的特殊性判定点P在双曲线右支上；第二次“细”用，利用（将4作为一般正数）导出点P横坐标存在的范围：

。

粗细结合，将已知条件运用得酣畅淋漓。

　　4、设椭圆的焦点为，P为椭圆上一点，的最大值为。

（1）求椭圆的离心率；

（2）设直线l与椭圆交于M、N两点，且直线l与圆心在原点，半径等于b的圆相切，已知线段MN长度的最大值为4，求椭圆方程和直线l的方程。

　　分析：

中的最大值为的最小值为，循着特殊与一般相互依存的辩证关系，想到从在中运用余弦定理推导的最小值切入。

　　解：

（1）设=，，，

　　则在中由余弦定理得

　　即　　　　　　　　　　　　　　　　①

　　∴的最小值为

　　又由题设知的最大值，即的最小值为

　　∴

　　∴　　即　　a=2b

　　∴

（2）由已知椭圆方程为　　　　　　　　　　②

　　由题设知直线l不垂直于x轴

　　设直线l的方程为　　　　　　　　　　　　　　③

　　设

　　则由直线l与圆相切得：

　　④

　　将③代入②得：

　　　　　　　　　　　　　　　　⑤

　　∴④代入⑤得

　　∴直线l与椭圆相交于不同两点

　　又由韦达定理得：

，　　⑥

　　∴

　　（当且仅当，即时等号成立）

　　∴的最大值为2b（当时取得）

　　∴由题设得　　（此时）　　　　⑦

　　∴a=2b=4　　　　　　　　　　　　　　　　　　　　⑧

　　进而由④得，即　　　　　　　　⑨

　　因此，由⑦、⑧、⑨得所求椭圆方程为，

　　直线l的方程为或

　　点评：

这里导出的①式为此类问题的共同基础：

设P为椭圆上任意一点，，则最小值为

　　据此若的最大值为，则（即）；

　　若的最大值为，则（即）；

　　若的最大值为，则（即）。

　　5、已知斜率为1的直线l与离心率为的双曲线交于P、Q两点，又直线l与y轴交于点R，且，，求直线和双曲线方程。

　　分析：

主要已知条件借助向量表出，故主要问题是认知已知条件，进而根据问题的具体情况进行推理或转化。

　　解：

由得，

　　∴双曲线方程为　　　　　　　　　　①

　　设，直线l的方程为　　　　②

　　将②代入①得　　　　　　③

　　对于方程③，恒成立

　　由韦达定理得　　　　　　　　　　　　　　④

　　　　　　　　　　⑤

　　∵

　　∴

　　即

　　由此得

　　又由题设得，故得　　　　　　　　　　⑥

　　∴由④、⑥联立解得　　　　　　　　　　　　⑦

　　将⑦代入⑤得　　　　　　　　　　　　　　　　⑧

　　再注意到得

　　　　　　　　　　　　　　⑨

　　∴将⑦、⑧代入⑨得

　　解得，　　　　　　　　　　　　　　⑩

　　∴

　　因此，由①，②得所求双曲线方程为，

　　所求直线方程为

　　点评：

　　（Ⅰ）关于此类直线与圆锥曲线相交的问题，对于交点坐标的处置适当与否，成为解题繁简成败的关键。

于是，围绕着对交点坐标的“解”与“设”的应用选择，产生出解题策略：

解而不设与设而不解；“既设又解”与“不设不解”。

在这里，我们对交点P、Q的坐标运用的是“既设又解”，请同学们注意品悟这里“解”的分寸的把握。

　　（Ⅱ）这里解题的层次分明，已知式一转化一代入一结论：

　　已知式（）→转化→代入→结论⑧；

　　已知式（）→转化→代入→结论⑩。

　　同学们应注意学习与追求这种解题的明晰与漂亮。

　　6、已知，

（1）求点P（x，y）的轨迹C的轨迹方程；

（2）若直线与曲线C交于A、B两点，D（0，-1），且有，试求m的取值范围。

　　分析：

　　对于

（1），从已知条件入手，利用向量的坐标表示进行推理；

　　对于

（2），此类关于直线与圆锥曲线相交的比较复杂的问题，要刻意向基本的弦中点或弦长问题转化。