第26课时图形的相似含答案Word文档下载推荐.docx
《第26课时图形的相似含答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《第26课时图形的相似含答案Word文档下载推荐.docx(14页珍藏版)》请在冰豆网上搜索。
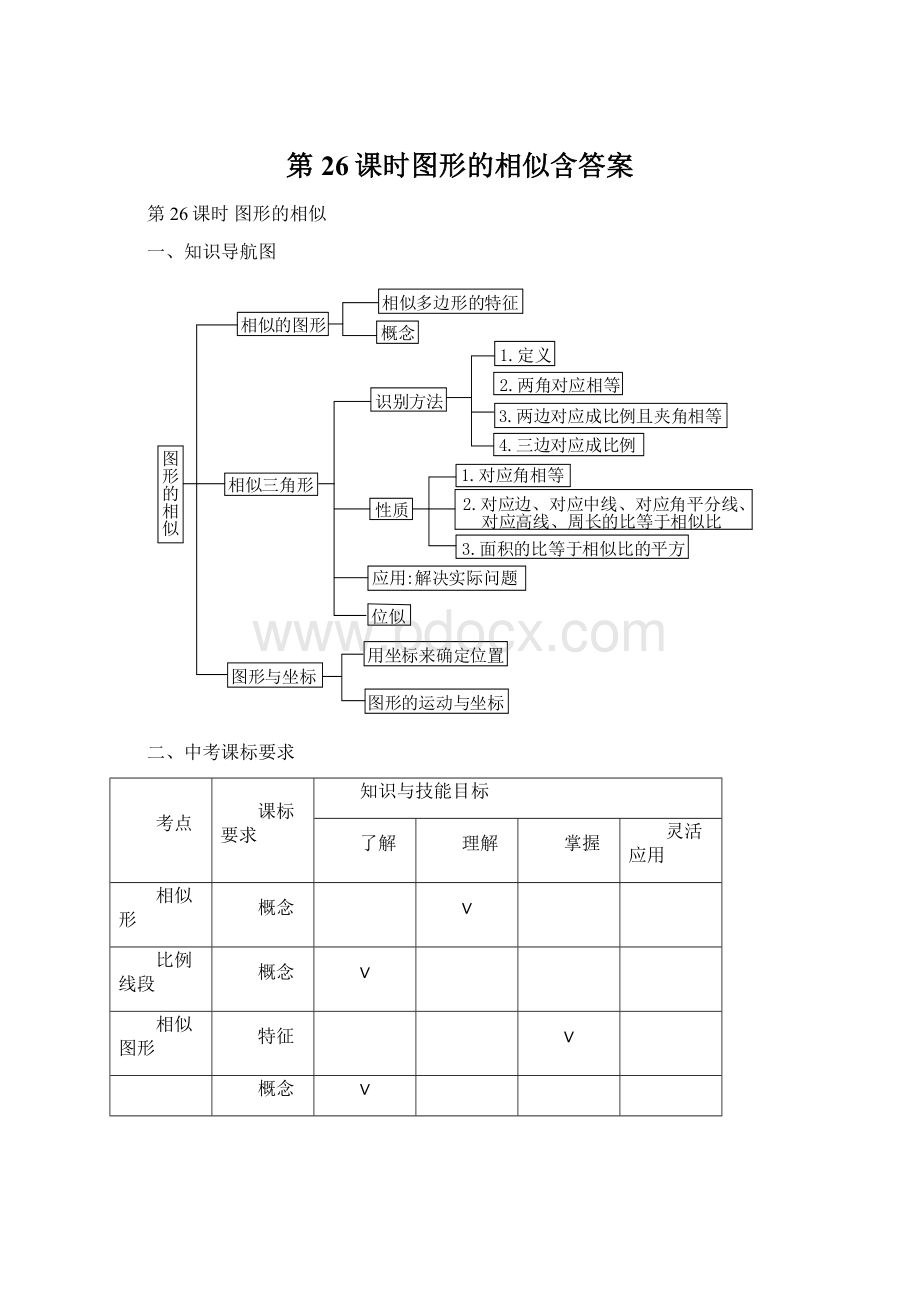
画法
图形与坐标
用坐标确定位置
图形的运动与坐标
三、中考知识梳理
1.比例线段
由于比例线段的实质就是四个正数组成的比例式,所以要学好本部分内容,首先要复习小学所学的有关比例的相关知识.
2.相似形
具有相同形状的图(大小不一定相同).
3.相似多边形的特征
“对应边成比例,对应角相等”既是相似多边形的识别方法又是性质.
4.相似比
相似比是把一个图形放大或缩小的倍数,其具有顺序性,全等是相似比为1时的特殊情况.
5.相似三角形的性质
(1)对应边成比例,对应角相等;
(2)对应高的比、对应中线的比、对应角平分线的比都等于相似比;
(3)周长的比等于相似比,面积的比等于相似比的平方.
6.相似图形的画法
是新课标中新增添的内容,要求掌握用多种方法将一个图形放大或缩小.
7.图形与坐标
是新课程中新增添的内容,应注意把“形”与“数”紧密地联系在一起.
四、中考题型例析
1.列比例式
例1(2002·
北京怀柔)已知三个数1,2,
请你再添上一个(只填一个)数,使它们能构成一个比例式,则这个数是_________.
分析:
这是一道开放型试题,由于题中没有告知构成比例的各数顺序,故应考虑各种可能位置.
答案:
2
或
。
2.相似三角形的识别
例2(2004·
昆明)如图,在△ABC中,AC>
AB,点D在AC边上(点D不与A、C重合),若再增加上条件就能使△ABD∽△ACB,则这个条件可以是_______.
解析:
由于所识别的两三角形隐含着一个公共角∠A,因此依照识别方法,只要再附加条件∠ABD=∠C,∠ADB=∠ABC,或
即可.
∠ABD=∠C,∠ADB=∠ABC,
3.比例式的证明
例3(2002·
安徽)如图,AD是直角△ABC斜边上的高,DE⊥DF,且DE和DF分别交AB、AC于E、F.
求证:
所证比例式中四条线段为△AFD与△BDE的边,只需证△AFD与△BDE相似即可.
证明:
∵∠BAC=90°
AD⊥BC,
∴∠B+∠C=90°
∠DAC+∠C=90°
.
∴∠B=∠DAC.
同理∠C=∠BAD.
又∵∠ADE+∠ADF=90°
∠CDF+∠ADF=90°
∴∠ADE=∠CDF.
又∵∠BED=∠BAD+∠ADE,∠AFD=∠C+∠CDF.
∴∠BED=∠AFD.
∴△BED∽△AFD.
∴
点评:
证明比例式或等积式的基本方法是证明包含比例式或等积式中的四条线段所在的两三角形相似.如果直接证明不容易,则可等线段转化或等比转化.
4.图形与坐标
例4图是某市旅游景点的示意图.试建立直角坐标系,用坐标表示各个景点的位置.
直角坐标系位置不同,各景点的坐标也不相同.如以中心广场为原点建立坐标系,答案如下:
解:
以中心广场为原点建立坐标系,如图1-14-3,则各景点坐标依次为:
雁塔(-2,4);
钟楼(-4,2),大成殿(-3,-1);
科技大学(-5,-4);
碑林(4,4);
映月湖(4,-3).
基础达标验收卷
一、选择题
1.(2004·
四川)如图,已知D、E分别是△ABC的AB、AC边上一点,DE∥BC,且S△ADE:
S四边形DBCE=1:
3,那么AD:
AB等于()
A.
;
B.
;
C.
D.
2.(2004·
上海)如图,在△ABC中,AB=AC,∠A=36°
BD平分∠ABC,DE∥BC,那么在下列三角形中,与△ABC相似的三角形是()
A.△DBEB.△ADEC.△ABDD.△BDC
3.(2002·
邵阳)下列判断错误的是()
A.矩形是平行四边形
B.相似三角形一定是全等三角形
C.等腰梯形的对角线相等D.两直线平行,同位角相等
4.(2002·
聊城)在△ABC中,AB=24,AC=18,D是AC上一点,AD=12,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为().
A.16B.14C.16或14D.16或9
二、填空题
1.(2003·
贵阳)若两个相似三角形的相似比是2:
3,则这两个三角形对应中线的比是__________.
2.(2003·
北京)如图,在等边三角形ABC中,点D、E分别在AB、AC边上,且DE∥BC.如果BC=8cm,AD:
AB=1:
4,那么△ADE的周长等于_________cm.
3.(2003·
杭州)如图,锐角三角形ABC的边AB、AC上的高线CE和BF相交于点D,请写出图中的两对相似三角形:
__________(用相似符号连接).
4.(2003.上海)在△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC,如果AC=10,AE=4,那么BC=________.
5.(2004·
青岛)观察下列图象,与图
(1)中的鱼相比,图
(2)中的鱼发生了一些变化,若图
(1)中鱼上点P的坐标为(4,3.2),则这个点在图
(2)的对应点P1的坐标应为________.
6.如图,张坚在某市动物园的大门口看到这个动物园的平面示意图,试借助刻度尺、量角器解决如下问题:
(1)建立适当的直角坐标系,用坐标表示猴山、驼峰、百鸟园的位置.
(2)填空:
百鸟园在大门的北偏东________度的方向上,到大门的距离约为_______cm.
熊猫馆在大门口的北偏东________度的方向上,到大门距离约为_______cm;
驼峰在大门的南偏西________度的方向上,到大门的距离约为________cm.
三、解答题:
(2003·
长沙)如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AF,F为AE上一点,且∠BFE=∠C.
△ABF∽△EAD.
能力提高练习
一、实际应用题
南京)在比例尺是1:
8000的南京市城区地图上,太平南路的长度约为25cm,它的实际长度约为()
A.320cmB.320mC.2000cmD.2000m
2.(2002·
南京)如图,测量小玻璃管口径的量具ABC上,AB的长为10mm,AC被分为60等份.如果小管口DE正好对着量具上30份处(DE∥AB),那么小管口径DE的长是______mm.
3.(2004·
武汉)如图,是束平行的阳光从教室窗户射入的平面示意图,光线与地面所成角∠AMC=30°
在教室地面的影长MN=
.若窗户的下檐到教室地面的距离BC=1m,则窗户的上檐到教室地面的距离AC为()
A.
mB.3mC.3.2mD.
m
淄博)为测一河两岸相对两电线杆A、B的距离,如图所示,有四位同学分别测量出了以下四组数据:
①AC,∠ACB;
②CD,∠ACB,∠ADB;
③EF,DE,AD;
④DE,DF,AD.能根据所测数据,求出A、B间距离的共有()
A.1组B.2组C.3组D.4组
二、学科内综合题
5.(2003.仙桃市、潜江市、天门市、江汉油田)在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,在如图所示5×
5的方格纸中,作格点△ABC和△OAB相似(相似比不能为1),则C点坐标是______.
6.(2004·
成都市郫县)在图的网格图中按要求画出图形,并回答问题:
(1)先画出△ABC向下平移5格后的△A1B1C1,再画出△ABC以点O为旋转中心,沿顺时针方向旋转90°
后的△A2B2C2;
(2)在与同学交流时,你打算如何描述
(1)中所画的△A2B2C2的位置?
三、跨学科应用题
7.(2003·
济南)检查视力时,规定人与视力表之间的距离为5m.如图
(1),现因房间两面墙的距离为3m,因此使用平面镜来解决房间小的问题.若使墙面镜子能呈现完整的视力表,如图
(2),由平面镜成像原理,作出了光路图,其中视力表AB的上下边沿A、B发出的光线经平面镜MM′的上下边沿反射后射入人眼C处,如果视力表的全长为0.8m,请计算出镜长至少为多少米?
(1)
四、开放探索题
8.(2004·
陕西)如图,矩形ABCD,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足()
A.a≥
bB.a≥bC.a≥
bD.a≥2b
9.(2004·
南京)如图,AB⊥BC,DC⊥BC,垂足分别为B、C.
(1)当AB=4,DC=1,BC=4时,在线段BC上是否存在点P,使AP⊥PD?
如果存在,求线段BP的长;
如果不存在,请说明理由.
(2)设AB=a,DC=b,AD=c,那么当a、b、c之间满足什么关系时,在直线BC上存在点P,使AP⊥PD?
一、1.C2.BD3.B4.D
二、1.2:
32.63.△BDE∽△CDF;
△ABF∽△ACE4.155.(4,2.2)6.略
三、证明:
∵四边形ABCD是平行四边形,
∴∠BAF=∠AED,∠C+∠D=180°
.
又∵∠C=∠BFE,∠BFE+∠BFA=180°
∴∠D=∠BFA.
∴△ABF∽△EAD.
1.D2.53.B4.D
5.(4,4),(5,2)
6.
(1)见图:
(2)说得合理即可.
7.作CD⊥MM′,垂足为D,并延长交A′B′于E.
∵AB∥MM′∥A′B′,∴CE⊥A′B′.
∴△CMM′∽△CA′B′.
又∵CD=5-3=2,CE=5,A′B′=AB=0.8,
∴MM′=0.32(m)
∴镜长至少为0.32m.
三、开放探究题
8.D
9.解:
(1)如果存在点P,使AP⊥PD,那么∠APD=90°
∴∠APB+∠CPD=90°
∵AB⊥BC,DC⊥BC,
∴∠APB+∠BAP=90,
∴∠BAP=∠CPD.
∵∠B=∠C=90°
∴∠APB=∠CDP.
∴△APB∽△PDC,∴
设BP=x,则PC=4-x.
∴x1=x2=2.
∴在线段BC上存在点P,使AP⊥PD,此时,BP=2.
(2)如果在直线BC上存在点P,使AP⊥PD,那么点P在以直线AD为直径的圆上,且圆的半径为
c.
取AD的中点O,过点O作OE⊥BC,垂足为E.(如图)
∵∠B=∠OEC=∠C=90°
∴AB∥OE∥DC.
∴AO=DO,∴BE=CE.
∴OE=
(AB+DC)=
(a+b).
∴当OE<
c,即a+b<
c时,以AD为直径的圆与直线BC相交.
此时,存在⊙O和直线BC的交点P1、P2,使AP1⊥P1D,AP2⊥P2D.
当OE=
c,即a+b=c时,以AD为直径的圆与直线BC相切.
此时,存在切点P,使AP⊥PD.
当OE>
c,即a+b>
c时,以AD为直径的圆与直线BC相离.
此时,在直线BC上不存在点P,使AP⊥PD.
综上,当a+b≤c时,在直线BC上存在点P,使AP⊥PD.