Lecture notes module 1文档格式.docx

Lecture notes module 1文档格式.docx

《Lecture notes module 1文档格式.docx》由会员分享，可在线阅读，更多相关《Lecture notes module 1文档格式.docx（34页珍藏版）》请在冰豆网上搜索。

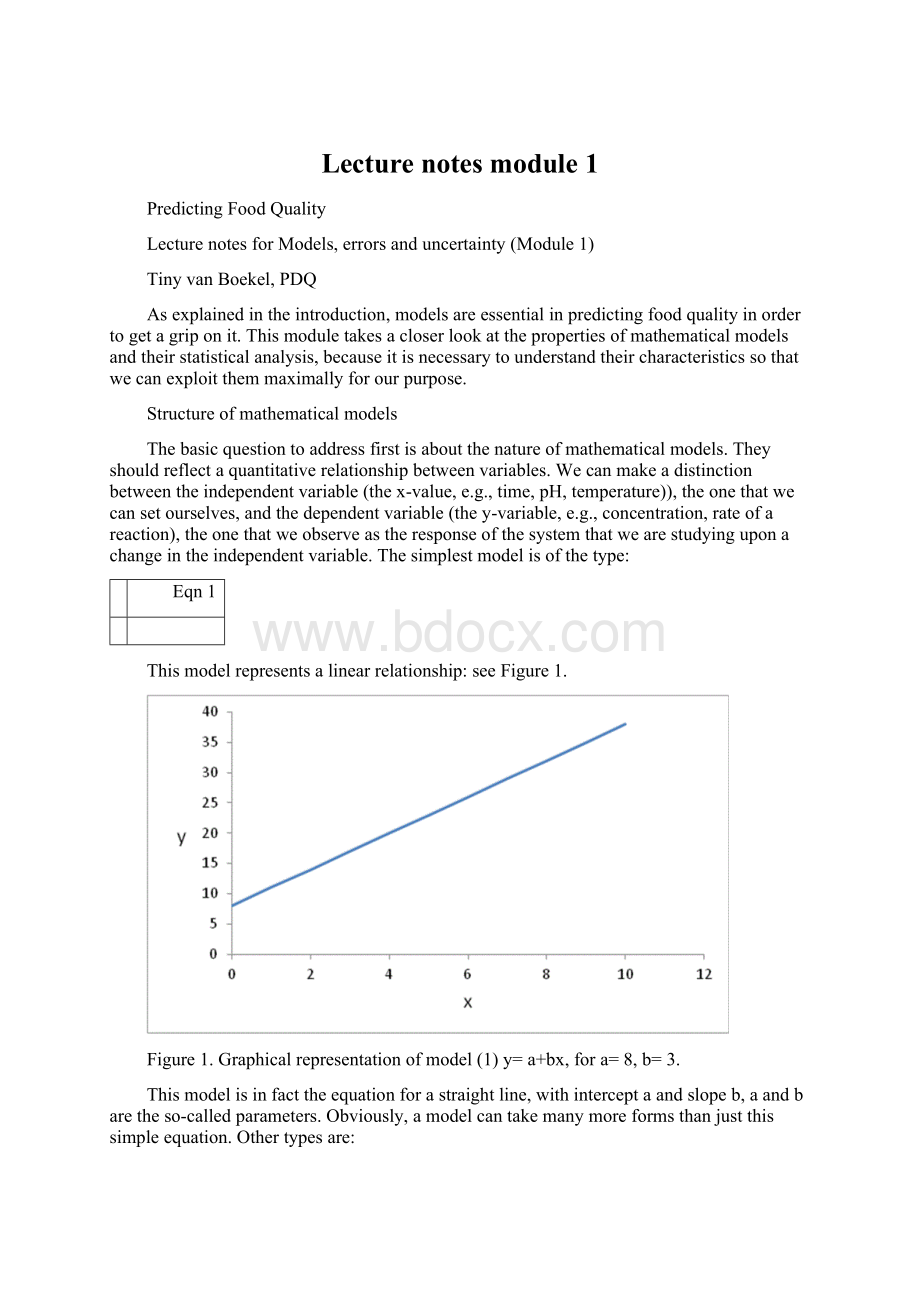
Figure1.Graphicalrepresentationofmodel

（1）y=a+bx,fora=8,b=3.

Thismodelisinfacttheequationforastraightline,withinterceptaandslopeb,aandbaretheso-calledparameters.Obviously,amodelcantakemanymoreformsthanjustthissimpleequation.Othertypesare:

Eqn2

Thismodeldisplaysanexponentialrelationship:

seeFigure2.

Figure2.Graphicalrepresentationofmodel（2:

）y=aexp（bx）fora=2,b=0.3（A）anda=10,b=-0.3（B）

AnothermodelisshowninFigure3,ahyperbola:

Eqn3

Figure3.Graphicalrepresentationofmodel（3）fora=3,b=1

Yetanothermodelisapolynomialoforder3,displayedinFigure4:

Eqn4

Figure4.Graphicalrepresentationofmodel（4）,fora=2,b=3,c=4.

So,typically,modelscontaintheindependent（thex-value）andthedependentvariable（they-value）andnexttothattheparameters（a,bandcintheaboveexamples）.Itistheparametersthatweareafter,theycontainspecificinformationabouttheunderlyingprocessthatweattempttodescribewithourmodel.

Togeneralize,anequationcanbewrittenas:

Eqn5

inwhichθrepresentsparameters（a,b,cintheaboveexamples）,ξrepresentstheindependentvariable（‘thex-value’）,andηthedependentorresponsevalue（theyvalue）.Equation（5）isthenotationforageneralmodelthatyouoftenfindinstatisticalliterature.

Howcanwefindasuitablemodelforourproblems?

Asstatedbefore,amodelshouldreflectaquantitativerelationbetweenanindependentandaresponsevariable.Weareverymuchdependentonexperimentalmeasurements;

thereisnogeneraltheorythatpredictshowrelationsshouldbeinfoods.（Thisisnottosaythattheoryisnotimportant,itdefinitelyisaswealsoshallseeinthiscourse,buttheavailabletheoryisnotsufficienttopredictquantitativerelations.）

Therefore,thefirstthingtodo,always,istosimplyplottheexperimentaldata,andseehowtherelationlookslike.Thiswillgiveanimportantclue,forinstancewhethertherelationislinearornon-linear,whetheritlookslikeahyperbolaoraparabola,etc.Themathematicalmodelsweneedinfood-scienceproblemsareusuallydescribingchangesintimeand/orspace,intheformof:

-Algebraicequations（suchastheonesdisplayedinequations（1–4）

-Differentialequationsoftheform

-Partialdifferentialequationsoftheform

Deterministicandstochasticmodels

Ifyoulookcloselyatsuchequations,youwillnoticethatforfixedvaluesoftheparametersthesameoutputy-valuewillalwaysbefoundforthesameinputxvalue.Thatmakesthemso-calleddeterministicmodels,thereisnouncertaintyinvolved,theoutputvaluesareexactlydeterminedbytheinputvalues.However,asmentionedbefore,weneedtoestimateparametersfromexperiments,andexperimentalvaluesarealwaysuncertaintosomeextent.Itisveryessentialtobeabletoestimatethisexperimentaluncertainty;

fortunatelywecandothatfromrepeatedexperiments.

Errorsanderrors

So,themodelsthatwearegoingtousearebaseduponexperimentalobservations.Experimentalobservationsalwayscontainunexplicableandunavoidableerrorandthereforealsothemodelsbasedupontheseexperimentswillbeuncertain,andsincewewanttousemodelstopredict,alsoourpredictionswillcontainacertainerror!

Thisistheveryreasonwhyweinsistsomuchondiscussingerrors:

theyarealwaysthereandweneedtocharacterizethemquantitatively.

Atthisstageitisimportanttospendattentiontotwoconceptsinrelationtomeasurements:

accuracyandprecision.Accuracyisabouthowclosemeasurementsaretotherealvalue.Thisisaphilosophicallyinterestingstatementbecausewedonotknowtherealvalue,weare,afterall,tryingtoestimateit!

Nevertheless,thereisareal,truevaluethatwewanttoapproximateascloseaspossible;

ifthereisaconstant,systematicdeviationbetweentheactualmeasurementandthe（unknown）truevaluethisiscalledasystematicerror.Accuracycanonlybeobtainedbycarefullycalibratinginstruments,solutions,weightingmeasurements,etc.,usingmaterialswithaknowncomposition.Thisisthefullresponsibilityoftheresearcherwhodoesthemeasurement.Statisticscannotcorrectforsystematicerrors!

Theotherconceptisofprecision:

howclosearethemeasuredvaluestogether,orhowstronglyaretheydispersed?

Thesearerandomerrorsthatoccurbychanceanduncontrolled.Youcanhaveanaccuratebutimprecisemeasurement,butalsoanimprecisebutaccuratemeasurement.Figure5givesanimpressionofthepossibilities.Thestatisticalmethodsthatwediscussinthiscourseareaboutprecision;

weassumethataccurateresultshavebeenobtainedorreportedinliterature,i.e.,withoutsystematicerror.Wealsoassumethatrandomerrorsaremeasuredandreported;

theyareeasilyidentifiedbydoingrepetitions.Unfortunately,manyliteraturesourcesdonotreporttheseerrorsveryclearly,whichmaybeconsideredacapitalsininscience!

Figure5.Aschematicrepresentationofaccuracyandprecision

Wecanmakeafurtherdivisioninthenatureofrandomerrors,namelyhomoscedasticandheteroscedasticerrors:

seeFigure6.

Figure6.Schematicrepresentationofhomoscedastic（A）andheteroscedasticerrors（B,C）.

Homoscedasticerrorsareerrorsthatdonotdifferwiththex-values,orinotherwords,theerrorsareapproximatelyconstantandindependentoftheindependentvariablex;

heteroscedasticerrorsdodependonthex-value.InFigure7Bthecaseisshownthattheerrorsinyincreasewithincreasingx.Itcould,inprinciple,bealsotheotherwayaround,asshowninFigure7C.Itisveryinstructivejusttoplotresultssothatitisimmediatelyobviouswhethertheerrorsarehomoscedasticornot.Theimportanceofknowingthisbecomesclearwhenwediscussregressiontechniquesinamoment.

Howtoestimateerrors?

Animportantconsequenceofexperimentaluncertaintyisthaterrorsarecarriedovertotheparameters.So,weareinneedofmodelsthatareabletoexpressthisuncertainty.Thatbringsusintotheareaofstochasticmodels.Equation（5）needstobeextendedasfollows:

Eqn6

Thetermεrepresentsthe“error”term（itisnotanerrorinthesensethatsomethingiswrong,itrepresentstheuncertaintywearefacedwith）.Howcanweputanumbertothiserrorterm?

Quitesimplyfromexperiments（afterhavingexcludedsystematicerrors,seeabove）:

repeatinganexperiment（notjustthemeasurementbutthewholetreatment!

）inexactlythesamewayshowstheuncontrollablevariation,andbydoingthatafewtimesthemeanandstandarddeviationcanbecalculated（preferablymorethantwotimesbecauseastandarddeviationbasedontwomeasurementsisquiteunreliable）.Experimentaluncertaintytypicallyreducesbydoingmorerepetitions（seebelow）.Nexttoexperimentaluncertaintythereisalsobiologicalvariation:

foodsarenaturalmaterialsandtheircompositionvaries:

twoapplesthatcomefromthesametreewillvarynevertheless.Thisisunavoidableandwecannotreduceit,butwecancharacterizeitviastatistics!

Thisleadstowell-knownparametersasthemean,standarddeviation,standarderror,confidenceintervals.Let’sshowsomeexamples.SupposeafoodchemistinLabAdeterminedthecalciumcontentofthesamemilkinfiverepetitions（n=5）,whileanotherfoodchemistdidthesamethinginLabBonthesamesampleofmilkbutnowwithtenrepetitions（n=10）:

Sampleno

Calciumcontent（mg/100gmilk）

LabA

LabB

1

117.7

121.4

2

119.5

114.6

3

121.3

116.1

4

117.6

120.9

5

110.2

109.3

6

7

117.3

8

119.8

9

116.6

10

123.5

Table1.Determinationsontheestimationofthecalciumcontentinmilkintwodifferentlabs

Notethatthisexperimentalsetupgivesinformationabouttheimprecisionofmeasuring.Itdoesnotgiveinformationaboutbiologicalvariationbecausethesamebatchofmilkwasanalysed.Forinformationaboutbiologicalvariabilityofcalciuminmilk,onewouldhavetoanalysesamplesfromdifferentbatches;

thevariabilityobservedinsuchacasewouldbethesumofthecontributionofthebiologicalvariability+theexperimentaluncertainty.

Forthepresentexample,thesamplemeanis:

Eqn7

Thisresultsin117.3mg/100gmilkforLabAand117.6mg/100gmilkforLabB.Notethatthemeansarenotexactlythesame,butquiteclose.

Thesamplevariancevis:

Eqn8

Thisresultsinv=17.8forLabAand16.6forLabB.

Thesamplevarianceisactuallythesumofsquaresdividedbythedegreesoffreedom;

onedegreeoffreedomislostbecausethemeanisesti