平面向量单元测试题含答案Word文件下载.docx
《平面向量单元测试题含答案Word文件下载.docx》由会员分享,可在线阅读,更多相关《平面向量单元测试题含答案Word文件下载.docx(12页珍藏版)》请在冰豆网上搜索。
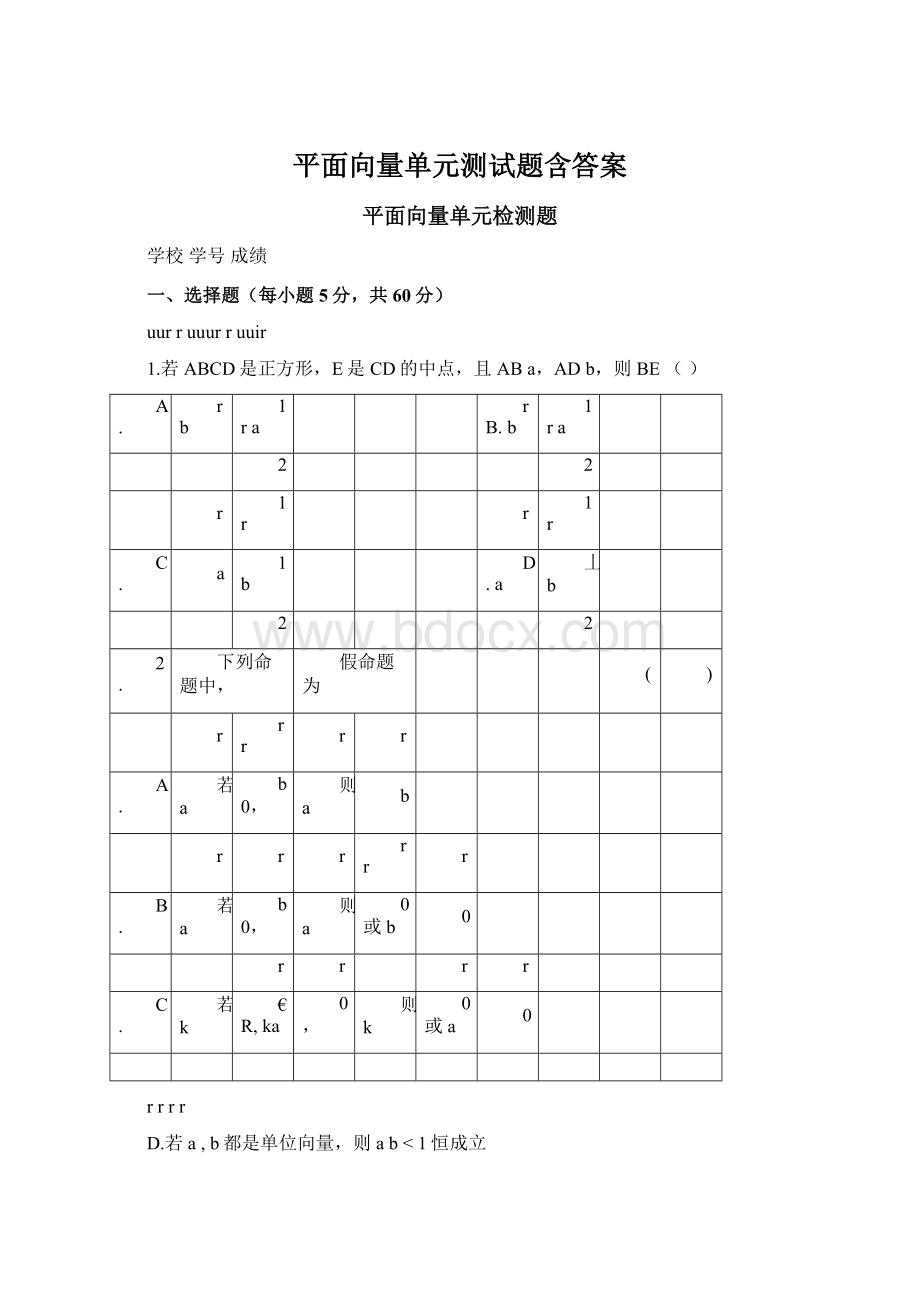
则k
0或a
rrrr
D.若a,b都是单位向量,则ab<
1恒成立
3.
设i,
b)
j是互相垂直的单位向量,向量r
(a
b),贝U实数m为
1)i
B.2
D.不存在
(m1)j,
D.
已知非零向量
4.
ra
ab,则下列各式正确的是
uurrurn
5.在边长为1的等边三角形ABC中,设BCa,CA
的值为
3
A.一
—
C.0
D.3
6.
在厶OAB中,
uuu
OA=(2cosa,2sina),
uuuruuu
OB=(5cosB,5sinB),若OA
uuur
OB
.3
C.5,3
5„3
uuurr
7.
在四边形
ABCD中,
ABa2b,
BC4ab,
CD
5a
3b,则四边形
ABCD
的形状是
()
长方形
平行四边形
C.菱形
梯形
8.
把函数y
cos2x
3的图象沿向量
a平移后得到函数
y
sin(2x
-)的图象,
则向
量
是a
3)
C.(—,3)
(-
3)
6
12
9.若点F1、
F2为椭圆Xy21
4
的两个焦点,
P为椭圆上的点,
当厶F1PF2的面积
为1时,
P^的值为
A.0
B.1
C.3
D.6
rrr
10.向量a=(-1,1),且a与a2b方向相同,贝Uab的围是()
A.(1,+x)B.(-1,1)C.(-1,+x)D.(-x,1)
11.O是平面上一点,A,B,C是该平面上不共线的三个点,一动点P满足
uuuuuuuuiruur
OPOA+(ABAC),入€(0,+x),则直线AP—定通过厶ABC的()
心
外心
C.重心
D.垂心
12.
已知
D是厶ABC中
AC边上
一占且AD
亠八、、‘-1_L-
22辽,/C45°
/ADB60,则
uuiT
DC
aB
DB
C.「3
D.1
—-
、填
〕空题(每小题
4分,
共16分)
13.△ABC中,已知a4,b6,sinB,则/A。
uuuuuuuu
14.已知M(3,4),N(12,7),点Q在直线MN上,且|QMMN|1:
3,则点Q的
坐标为。
rrrrrr
15.已知|a|=8,|b|=15a+b|=17,贝Ua与b的夹角为
16.给出下列四个命题:
1若|ab||a||b|,则a//b;
rrrrrrr
2(bc)a(ca)b与c不垂直;
uuiruuu
3在△ABC中,三边长BC5,AC8,AB7,则BCCA20;
4设A(4,a),B(b,8),C(a,b),若OABC为平行四边形(0为坐标原点)
/AOC=
其中真命题的序号是(请将你正确的序号都填上)。
三、解答题(74分)
uuuOB,
uuuuuuuur
17.(本小题满分12分)设向量0A=(3,1),OB=(1,2),向量0C
uuiTuuuuuiTuuuuuuuuu
BC//OA,又OD+OA=OC,求OD。
18.(本小题满分12分)已知A(2,0),B(0,2),C(cos,sin),(0uuuuuiT_uuuuuiT
(1)若|OAOC|「7(O为坐标原点),求OB与OC的夹角;
uuuuuir
(2)若ACBC,求tan的值。
19.(本小题满分12分)
uuuruuuruuuruuuruuurruuurr
如图,O,A,B三点不共线,OC2OA,OD3OB,设OAa,OBb。
rruuur
(1)试用a,b表示向量OE;
(2)设线段AB,OECD的中点分别为
L,MN,试证明L,MN三点共线。
uuuruuuruuur
20.(本小题满分12分)在直角坐标系中,A(1,t),C(-2t,2),OBOAOC(O是坐标原点),其中t€(0,+x)。
⑴求四边形OAB(在第一象限部分的面积S(t);
⑵确定函数S(t)的单调区间,并求S(t)的最小值。
21.(本小题满分12分)
如图,一科学考察船从港口0出发,沿北偏东角的射线0Z方向航行,其中
1
在距离港口Q为3,T3a(a为正常数)海里北偏东角的A处有一个供给科学考察船物资的
小岛,其中cos。
现指挥部紧急征调沿海岸线港口0正向m海里的B处的补给船,
413
速往小岛A装运物资供给科学考察船,该船沿BA方向不变全速追赶科学考察船,并在C处相遇。
经测算,当两船运行的航线0Z与海岸线0B围成的三角形OBQ面积S最小时,补给最合适。
(1)求S关于m的函数关系式S(m);
(2)当m为何值时,补给最合适?
22.(本小题满分14分)
已知在直角坐标平面上,向量a=(-3,2入),b=(-3入,2),定点A(3,0),其中0<入<1。
一自点A发出的光线以a为方向向量射到y轴的B点处,并被y轴反射,其反射光线
与自点A以b为方向向量的光线相交于点P。
(1)求点P的轨迹方程;
(2)问ABP、0四点能否共圆(0为坐标原点),并说明理由。
平面向量答案
一、选择题:
本大题共12小题,每小题5分,共60分。
1.B;
2.B;
3.A;
4.D;
5.B;
6.D;
7.D;
8.A;
9.A;
10.C;
11.C;
12.B
―I-―h—*■―*f—*—*■*1—B-
10.C.解析:
注意a与a+2b同向,可设a+2b=Xa(入>0),贝Ub=a,从而
-“1-2
aba10。
F■]1Ni+]■!
■■+
11.C.解析:
OPOA+(ABAC),即AP(ABAC),即AP与ABAC同向。
12.B.解析:
解三角形可得/ABD=90。
二、填空题:
本大题共4小题,每小题4分,共16分。
13.30°
14.(6,5)或(0,3)15.-16.①④
三、解答题:
本大题共6小题,共74分。
17.(本小题满分12分)
解:
设OC=(x,y),
■/OCOB,•OCOB0,•2y-x=0,①
(0,
sin
19.(本小题满分12分)
⑴tB,E,C三点共线,二OE=xOC+(1-x)OB=2xa+(1-x)b,①
同理,:
A,E,
D三点共线,
可得,
OE=ya+3(1-y)b,②
比较①,②得,
2xy,
1x3(1
y)解得
_2
x=5,
y=5
,二OE=4a?
b。
55
(2)vOLa
2oe
4a3b
10
ON
1(OCOD)笃色,
22
ML
OLOM
2b
•••MN6ML,二L,M,N三点共线。
20.(本小题满分12分)
(1)tOBOAOCOAB(为平行四边形,
又•OAOC0,二OALOC二四边形OABC为矩形。
•••OBOAOC=(1-2t,2+t),
1当1-2t>
0,即0<
t<
丄时,A在第一象限,B在第一象限,C在第二象限,(如图1)
此时BC的方程为:
y-2=t(x+2t),令x=0,得BC交y轴于K(0,2t2+2),
•••S(t)=SOABCS△OK(=2(1-t+t2-t
2当1-2t<
0,即t>
丄时,A在第一象限,B在y轴上或在第二象限,C在第二象限,
(如图2)
此时AB的方程为:
y-t=
(x-1),令x=0,得AB交轴于M(0,t+-),
/.S(t)=S△OA=(t
1).
2(1
•••S(t)=
2(t
tt2
t3),(0
》,(t
(2)当0<
1时,
•••S(t)在(0,-)
S(t)=2(1-t+t2-t3),S'
(t)=2(-1+2t-3t2)<
0,
上是减函数。
当t>
丄时,S(t)=
1111
-(t[),s,(t)=列戶,
•••S(t)在[―,1]上是减函数,在(1,+X)上是增函数2
•••当t=1时,S(t)有最小值为1。
(1)以0为原点,正北方向为轴建立直角坐标系。
直线0Z的方程为y=3x,①
•A(9a,6a)。
由①、②解得,c(公丄
m7am7a
•S(m)=S^ob=1|OB||yc|=型,(m7a)。
2m7a
(2)S(m)=3a[(m-7a)+14a]>
84a2。
m7a
当且仅当m-iaM-49^,即m=14i>
7a时,等号成立,m7a
故当m=1Q为海里时,补给最合适。
(1)设P(x,y),A关于原点的对称点为C,则C(-3,0)。
依题意,B(0,2入),•CB(3,2),CP(x3,y),
由反射光线的性质,C,B,P三点共线,•3y-2入(x+3)=0,①
•••AP(x3,y),且AP//b,•3入y+2(x-3)=0,②
由①,②消去入得P点轨迹方程为:
—1,(x,y>
0)。
94
(2)若A、B、P、O四点共圆,则/P=ZAOB=90,
22
•APCP0,•x2-9+y2=0,又—-1,可得y=0,矛盾。
•A、B、P、O四点不能共圆。