七上数学方程教案文档格式.docx

七上数学方程教案文档格式.docx

《七上数学方程教案文档格式.docx》由会员分享，可在线阅读，更多相关《七上数学方程教案文档格式.docx（36页珍藏版）》请在冰豆网上搜索。

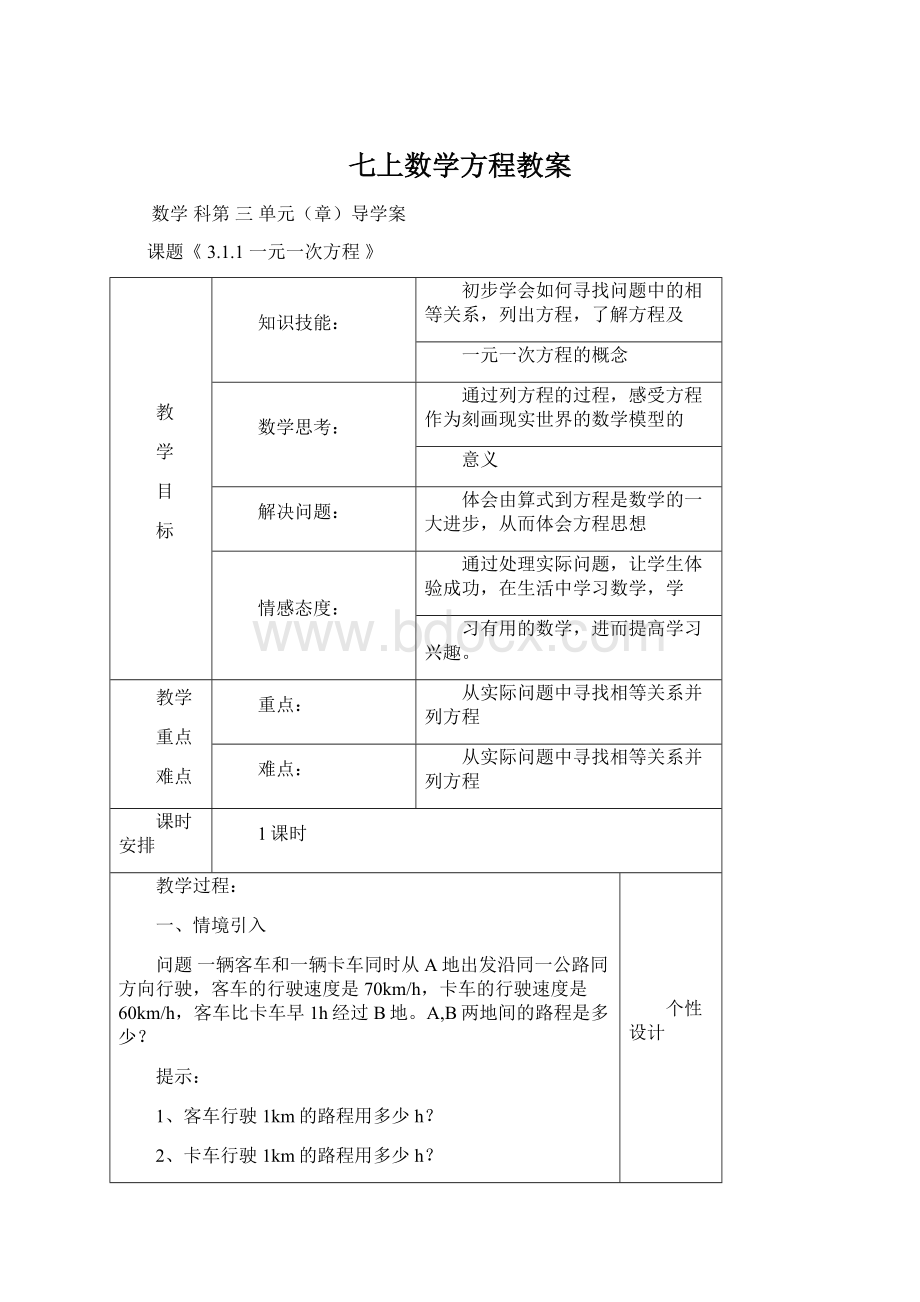
1、客车从A地到B地的行驶时间为多少h？

2、卡车从A地到B地的行驶时间为多少h？

3、因为客车比卡车早1h经过B地，所以___比____小1．

方法2：

如果设客车到达B地要用xh，则卡车到达B地所用的时间应该是多少h？

用含x的式子表示关于路程的数量：

1、客车从A地到B地行驶的路程为多少km？

2、卡车从A地到B地行驶的路程为多少km？

3、因为客车与卡车从A地到B地的总行程是相等的，所以等于．

列方程时，要先设字母表示未知数，然后根据问题中的相等关系，

写出含有未知数的等式——方程

三、讨论、探究、交流

例1根据下列问题，设未知数并列出方程：

（1）用一根长24cm的铁丝围成一个正方形，正方形的边长是多少？

（2）一台计算机已使用1700小时，预计每月再使用150小时，经过多少月这台计算机的使用时间达到规定的检修时间2450小时？

（3）某校女生占全体学生数的52%，比男生多80人，这个学校有多少学生？

观察上面列出的方程有什么共同特点？

只含有一个未知数（元），未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程。

四、练习巩固

1：

判断下列式子是方程吗？

如果是，哪些又是一元一次方程呢，为什么？

（1）2x+1

（2）2m+15=3

（3）3x-5=5x+4（4）-3x+1.8=3y

（5）3a+9>

15

某班开展为贫困山区学校捐书活动，捐的书比平均每人捐3本多21本，比平均每人捐4本少27本，求这个班有多少名学生？

如果设这个班有x名学生，请列出关于x的方程．

五、小结

用方程的方法来解决实际问题，一般要经历哪几个步骤？

（1）用字母表示问题中的未知数（通常用x,y,z等字母）；

（2）根据问题中的相等关系，列出方程．

分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法

板书设计：

3.1.1一元一次方程

当堂练习：

判断下列各式是不是方程，是的打“√”，不是的打“ｘ”并说明原因。

（1）-2+5=3（）

（2）3χ-1=7（）

（3）m=0（）（4）χ﹥3（）

（5）χ+y=8（）（6）2χ2-5χ+1=0（）

（7）2a+b（）（8）x=4（）

2.下列各式中，哪些是一元一次方程？

（1）5x=0

（2）1+3x

（3）x+y=5

（4）3x+6=3x-5

设计者：

审查者：

日期：

2016年10月20日

课题《3.1.2等式的性质》

了解等式的两条性质

应用等式的性质把简单的一元一次方程化成“x=a”

会用等式的性质解简单的（用等式的一条性质）一元一次方程

培养学生观察、分析、概括及逻辑思维能力

理解和应用等式的性质.

第1课时

（一）创设情景导入新课

用估算的方法我们可以求出简单的一元一次方程的解．你能用这种方法求出下列方程的解吗？

（1）3x-5＝22；

（2）0.28-0.13y=0.27y＋1.

第

（1）题要求学生给出解答，第

（2）题较复杂，估算比较困难，此时教师提出：

我们必须学习解一元一次方程的其他方法．

（二）合作交流解读探究

①实验演示：

教师先提出实验的要求：

请同学们仔细观察实验的过程，思考能否从中发现规律，再用自己的语言叙述你发现的规律．然后按教科书第81页图3.1-2的方法演示

实验．

教师可以进行两次不同物体的实验．

②归纳：

请几名学生回答前面的问题．

在学生叙述发现的规律后，教师进一步引导：

等式就像平衡的天平，它具有与上面的事实同样的性质．比如“8=8”，我们在两边都加上6，就有“8＋6=8＋6”；

两边都减去11，就有“8－11=8－11”.

③表示：

问题1：

你能用文字来叙述等式的这个性质吗？

在学生回答的基础上，教师必须说明：

等式两边加上的可以是同一个数，也可以是同一个式子．

问题2：

等式一般可以用a=b来表示．等式的性质1怎样用式子的形式来表示？

如果a=b，那么a±

c=b±

c

字母a、b、c可以表示具体的数，也可以表示一个式子。

④观察教科书第81页图3.1－3，你又能发现什么规律？

你能用实验加以验证吗？

在学生观察图3.1－3时，必须注意图上两个方向的箭头所表示的含义．观察后再请一名学生用实验验证．

然后让学生用两种语言表示等式的性质2.

如果a=b，那么ac=bc

如果a=b（c≠0），那么

（三）应用迁移巩固提高

方程是含有未知数的等式，我们可以运用等式的性质来解方程。

例教科书第82页例2．

分析：

所谓“解方程”，就是要求出方程的解“x=？

’’因此我们需要把方程转化为“x=a（a为常数）”形式。

归纳一下解一元一次方程的依据和结果的形式．

（四）总结反思拓展升华

主要从以下几个方面去归纳：

①等式的性质有那几条？

用字母怎样表示？

字母代表什么？

②解方程的依据是什么？

最终必须化为什么形式？

③在字母与数字的乘积中，数字因数又叫做这个式子的系数．

3.1.2等式的性质

等式的性质1

等式的性质2

所谓“解方程”，就是要求出方程的解“x=？

①分别说出下列各式子的系数

3x，－7m，，a，－x，

②利用等式的性质解下列方程

（1）x－5=6

（2）0.3x=45

（3）－y=0.6

③七年级3班有18名男生，占全班人数的45%，求七年级3班的学生人数。

2016年10月21日

数学科第三单元（章）导学案

课题《3.2解一元一次方程

（一）——合并同类项与移项》

经历运用方程解决实际问题的过程，体会方程是刻画现实世界的有效数学模型．

探究如何将“ax＋bx=c”类型的一元一次方程转化为x=a。

学会合并（同类项），会解“ax＋bx=c”类型的一元一次方程．

能够找出实际问题中的已知数和未知数，分析它们之间的数量关系，列出方程．

建立方程解决实际问题，会解“ax＋bx=c”类型的一元一次方程

分析实际问题中的已知量和未知量，找出相等关系，列出方程

约公元825年，中亚细亚数学家阿尔—花拉子米写了一本代数书，重点论述怎样解方程．这本书的拉丁文译本取名为《对消与还原》．“对消”与“还原”是什么意思呢？

通过下面几节课的学习讨论，相信同学们一定能回答这个问题．

出示教科书86页问题1：

某校三年共购买计算机140台，去年购买数量是前年的2倍，今年购买的数量又是去年的2倍。

前年这个学校购买了多少台计算机？

（二）合作交流解读探究

引导学生回忆：

设问1：

如何列方程？

分哪些步骤？

师生讨论分析：

①设未知数：

前年购买计算机x台

②找相等关系：

前年购买量＋去年购买量＋今年购买量=140台

③列方程：

x＋2x＋4x=140

设问2：

怎样解这个方程？

如何将这个方程转化为x=a的形式？

学生观察、思考：

根据分配律，可以把含x的项合并，即

x＋2x＋4x=（1＋2＋4）x=7x

设问3：

以上解方程“合并”起了什么作用？

每一步的根据是什么？

学生讨论、回答，师生共同整理：

“合并”是一种恒等变形，它使方程变得简单，更接近x=a的形式。

对于问题1还有不同的未知数的设法吗？

学生思考回答：

若设去年购买计算机x台，得方程

若设今年购买计算机x台，得方程

例1解方程7x-2.5x+3x-1.5x=-15*4-6*3

先合并同类项，再将系数化为1。

（三）应用迁移巩固提高

教科书87页例2

（四）总结反思拓展升华

提问：

1、你今天学习的解方程有哪些步骤，每一步依据是什么？

、今天讨论的问题中的相等关系有何共同特点？

学生思考后回答、整理：

①解方程的步骤及依据分别是：

合并和系数化为1

②总量=各部分量的和

3.2解一元一次方程

（一）——合并同类项

1、解下列方程

（1）5x-2x=9

（2）0.5x+1.5x=7

（3）-3x+0.5x=10

（4）7x-4.5x=2.5*3-5

2、一个黑白足球的表面一共有32个皮块，其中有若干块黑色五边形和白色六边形，黑、白皮块的数目之比为3：

5，问黑色皮块有多少？

2016年10月22日

通过分析实际问题中的数量关系，建立方程解决问题，进一步认识方程模型的重要性．

建立方程解决实际问题，会解“ax＋b=cx+d”类型的一元一次方程

掌握移项方法，学会解“ax＋b=cx+d”类型的一元一次方程，理解解方程的目标.

体会方程解法中蕴涵的化归思想．

分析实际问题中的相等关系，列出方程.

第2课时

教科书88页问题2：

把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；

如果每人分4本，则还缺25本．这个班有多少学生？

引导学生回顾列方程解决实际问题的基本思路．

学生讨论、分析：

1、设未知数：

设这个班有x名学生

2、找相等关系：

这批书的总数是一个定值，表示它的两个等式相等．

3、列方程：

3x＋20=4x-25…

（1）

设问1：

它与上节课遇到的方程有何不同？

方程的两边都有含x的项（3x与4x）和不含字母的常数项（20与－25）．

怎样才能使它向x=a的形式转化呢？

学生思考、探索：

为使方程的右边没有含x的项，等号两边同减去4x，为使方程的左边没有常数项，等号两边同减去20.

3x－4x=－25－20…

（2）

以上变形依据是什么？

等式的性质1。

归纳：

像上面那样把等式一边的某项变号后移到另一边，叫做移项。

师生共同完成解答过程。

设问4：

以上解方程中“移项”起了什么作用？

通过移项，含未知数的项与常数项分别位于方程左右两边，使方程更接近于x=a的形式。

（三）应用迁移巩固提高

例3解方程3x+7=32-2x

移项、合并、系数化为1

1、今天你又学会了解方程的哪些方法？

有哪些步聚？

每一步的依据是什么？

2、现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗？

3、今天讨论的问题中的相等关系又有何共同特点？

①解方程的步骤及依据分别是：

移项（等式的性质1）

合并（分配律）

系数化为1（等式的性质2）

②“对消”与“还原”就是“合并”与“移项”

③表示同一量的两个不同式子相等。

3.2解一元一次方程

（一）——移项

把等式一边的某项变号后移到另一边，叫做移项。

（1）x-3=1.5x+1

（2）6x-7=4x-5

（3）0.5x-6=0.75x

2、有一个班的同学去划船，他们算了一下，如果增加一条船，正好每条船坐6人，如果送还和了一条船，正每条船坐9人，问这个班共多少同学？

2016年10月24日

数学科第单元（章）导学案

经历运用方程解决实际问题的过程，发展抽象、概括、分析和解决问题的能力。

探索并发现实际问题中的等量关系，并列出方程。

学会探索数列中的规律，建立等量关系。

能正确地求解一元一次方程并判断解的合理性。

建立一元一次方程解决实际问题。

第3课时

前几节课，我们讨论了用一元一次方程解决一些实际问题，其实许多数列、游戏活动中也蕴含着方程知识。

教科书87页例2：

有一列数，按一定规律排列成1，－3，9，－27，81，－243……其中某三个相邻数的和是－1701，这三个数各是多少？

观察这列数有什么规律？

（从符号和绝对值两方面）

学生讨论后发现：

后面一个数是前一个数的－3倍。

师生共同分析，完成解答过程：

解：

设这三个相邻数中的第一个数为x,则第2个数为－3x，第3个数为－3×

（－3x）=9x

根据这三个数的和是－1710，得

x－3x＋9x=－1710

合并，得7x=－243

所以－3x=729

9x=－2187

答：

这三个数是－243、729、－2187

引导学生讨论以上列方程解决实际问题的关键。

探索规律，找出相等关系

如有学生提出不同的设未知数的方法，同样给予鼓励。

（三）应用迁移巩固提高

1、三个连续的奇数的和是27，求这三个奇数。

2、如果三个连续奇数的和是29，你能求出这三个奇数吗？

3、教科书90页例4

4、用一元一次方程解决移动电话收费问题

（1）“全球通”移动电话的计费方法是:

月租费50元/月,本地通话费0.40元/分.一个月内,若通话200分,需交费_________元;

若通话x分,需交费__________元.

（2）李老师5月份“全球通”移动电话消费130元,求通话的时间是多少分.

全球通

神州行

月租费

50元/月

本地通话费

0.40元/分

0.60元/分

①你是怎样分析数列中的规律的？

②你学会判明方程的解是否合理吗？

③试用自己的话概括“用一元一次方程分析和解决实际问题”的一般过程。

学生思考、讨论、整理。

3.2解一元一次方程

（一）——合并同类项与移项

用一元一次方程解含多个未知数的问题时，通常先设其中一个为x，再根据其他未知数与x的关系，用含x的式表示这些未知数。

“全球通”和“神州行”两种移动电话的收费方式如表:

用“全球通”每月收月租费50元/月,此外根据累计通话时间按0.40元/分加收通话费.用“神州行”，不收月租费,根据累计通话时间按0.60元/分收通话费.

（1）若一个月内在本地通话100分,按两种计费方式各需交多少元?

选择哪一种计费方式比较便宜?

通话时间若是300分呢?

（2）若累计通话t分,则用“全球通”要收费__________元;

用“神州行”要收费__________元.

（3）当本地通话时间是多少分时,两种收费方式的收费一样?

（4）你认为在什么条件下选择“神州行”更便宜?

（5）请为你的家长在“全球通”和“神州行”两种移动电话的收费方式中选择一种,并说明理由.

2016年10月23日

课题《3.3解一元一次方程

（二）──去括号与去分母》

掌握用一元一次方程解决实际问题的方法，会用分配律，去括号解决关于含括号的一元一次方程．

建立等量关系．

经历应用方程解决实际问题的过程，发展分析问题，解决问题的能力，进一步体会方程模型的作用

关注学生在建立方程和解方程过程中的表现，发展学生积极思考的学习态度以及合作交流的意识．

列方程解决实际问题，会解含有括号的一元一次方程．

列方程解决实际问题．

一、引入新课

我们已经学习了运用一元一次方程解决一些比较简单的实际问题．本节继续讨论如何列、解一元一次方程的问题．当问题中数量关系较复杂时，列出的方程的形式也会较复杂，解方程的步骤也相应更多些．

问题：

某工厂加强节能措施，去年下半年与上半年相比，月平均用电量减少2000度，全年用电15万度，这个工厂去年上半年每月平均用电多少度？

你会用方程解这道题吗？

提出问题，学生思考，并与同伴交流，探索列方程思路．在学生充分思考、交流后，引导学生作以下分析：

1．本问题的等量关系是什么？

2．如果设上半年每月平均用电x度，那么怎样表示下半年每月平均用电量、上半年共用电量和下半年共用电量．

3．根据等量关系，列出方程．

4．怎样解这个方程．

等量关系是：

上半年用电量（度）＋下半年用电量（度）＝150000

设上半年每月平均用电x度，则下半年每月平均用电（x-2000）度，上半年共用电6x度，下半年共用电6（x-2000）度，列方程

6x+6（x-2000）=150000

去括号，得6x+6x-12000=150000

移项，得6x+6x=150000+12000

合并同类项，得12x=162000

系数化为1，得x=13500

因此，这个工厂去年上半年平均每月用电13500度．

思考：

本题还有其他列方程的方法吗？

用其他方法列出的方程应怎样解？

如果设去年下半年平均每月用电x度，那么怎样列方程呢？

这个方程的解是问题的答案吗？

设去年下半年平均每月用电x度，则上半年平均每月用电（x+2000）度，列方程，6（x+2000）+6x=150000．解方程，得x=11500，那么上半年平均每月用电量为11500+2000=13500（度）．

方法一叫直接设元法，方程的解就是问题的答案；

方法二是间接设元法，方程的解并不是问题答案，需要根据问题中的数量关系求出最后答案．

方程中有带括号的式子时，利用分配律去括号是常用的化简步骤．

二、范例学习

例1．解方程：

3x-7（x-1）=3-2（x+3）．

强调去括号时，要注意的事项．

三、巩固练习

1．解下列方程;

（1）4x+3（2x-3）=12-（x+4）

（2）6（0.5x-4）+2x=7-（

x-1）

（1）去括号，得4x+6x-9=12-x-4

移项，得4x+6x+x=12-4+9

合并，得11x=17

系数化为1，得x=

（2）去括号，得3x-24+2x=7-

x+1

移项，得3x+2x+

x=7+1+24

合并，得5

x=32

系数化为1，得x=6

用分配律去括号时，不要漏乘括号中的项，并且不要搞错符号．

方程中有多重括号时，一般应按先去小括号，再去中括号，再去大括号的顺序去括号．

四、课堂小结

本节课我们继续讨论列方程解决实际问题，同时学习了如何解含有括号的方法，解此类方程，一般地先去括号，后移项，合并，系数化为1，并且注意去括号时易出错的问题．

3.3解一元一次方程

（二）──去括号

解含有括号的方程：

一般地先去括号，后移项，合并，系数化为1，并且注意去括号时易出错的问题．

一、解方程．

（1）-5（x+1）=

；

（2）2-（1-y）=-2；

（3）5-（x-1）=3-3x；

（4）3-2（2x+1）=2（x-3）；

（5）4x-3（20-x）=6x-7（9-x）．

二、解答题．

甲、乙两人沿东西公路，自西向东匀速前进，甲每小时走3千米，乙每小时比甲多走2千米，甲在上午10点钟经过A地，乙在当天中午12点时经过A地，问乙下午几时追上甲？

追及地点距A多远？

2016年10月5日

进一步掌握列一元一次方程解应用题的方法步骤．

分析行程问题中顺流速度、逆流速度、水流速度、静水中的速度的关系，以及问题中的等量关系

运用方程解决实际问题，体会方程模型的作用．

培养学生自主探究和合作交流意识和能力，体会数学的应用价值．

分析问题中的数量关系，找出能够表示问题全部含义的相等关系，列出一元一次方程，并会解方程．

找出能够表示问题全部含义的相等关系，列