内蒙古中考数学重点题型专项训练二次函数综合题.docx
《内蒙古中考数学重点题型专项训练二次函数综合题.docx》由会员分享,可在线阅读,更多相关《内蒙古中考数学重点题型专项训练二次函数综合题.docx(41页珍藏版)》请在冰豆网上搜索。
内蒙古中考数学重点题型专项训练二次函数综合题
二次函数综合题
类型一与角度有关的问题
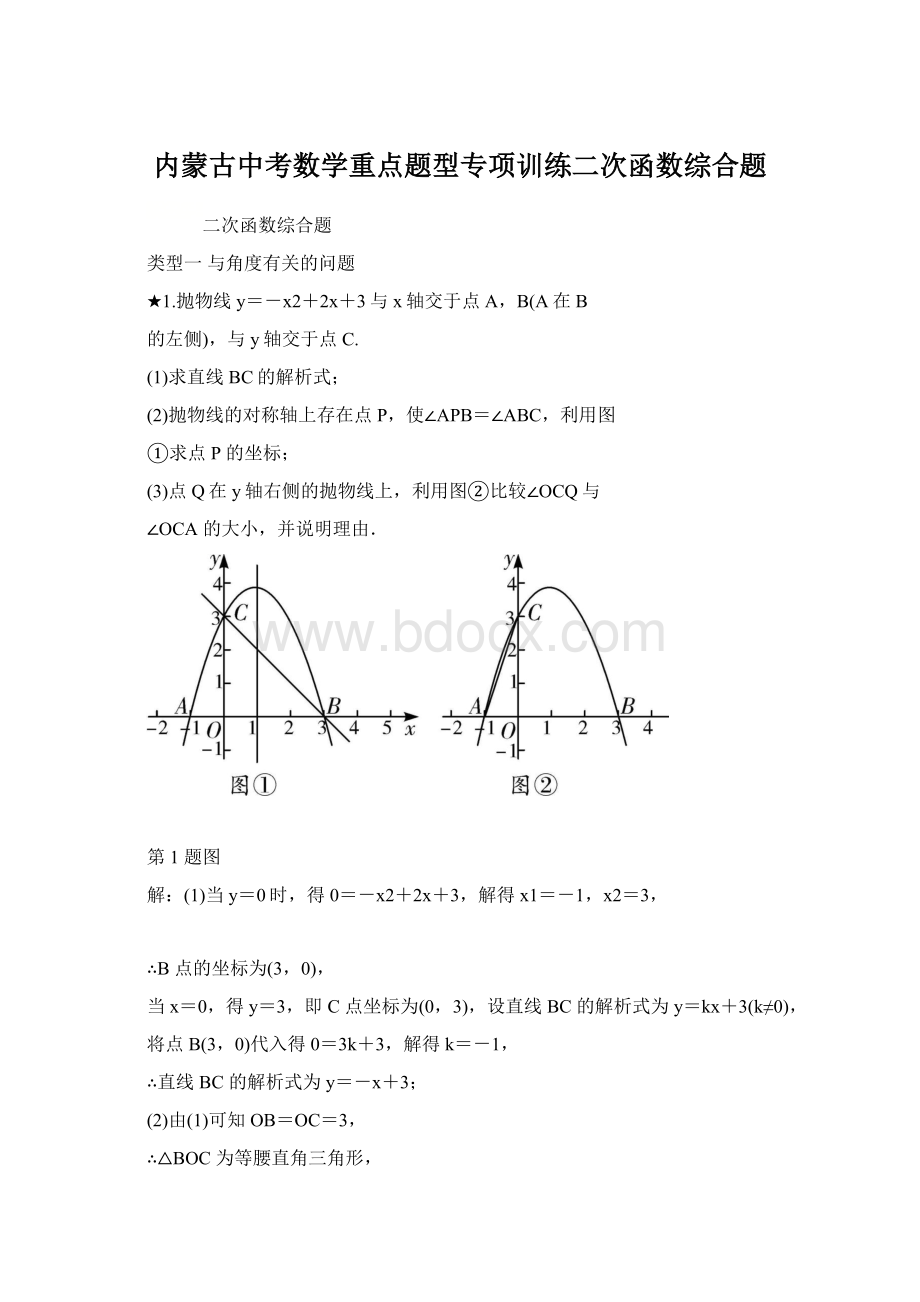
★1.抛物线y=-x2+2x+3与x轴交于点A,B(A在B
的左侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图
①求点P的坐标;
(3)点Q在y轴右侧的抛物线上,利用图②比较∠OCQ与
∠OCA的大小,并说明理由.
第1题图
解:
(1)当y=0时,得0=-x2+2x+3,解得x1=-1,x2=3,
∴B点的坐标为(3,0),
当x=0,得y=3,即C点坐标为(0,3),设直线BC的解析式为y=kx+3(k≠0),
将点B(3,0)代入得0=3k+3,解得k=-1,
∴直线BC的解析式为y=-x+3;
(2)由
(1)可知OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠ABC=45°,
抛物线对称轴为x=1,
设抛物线对称轴交直线BC于点D,交x轴于点E,
当点P在x轴上方时,如解图①,
第1题解图①
∵∠APB=∠ABC=45°,且PA=PB,
∴∠PBA=180°-45°=67.5°,
2
∠DPB=12∠APB=22.5°,
∴∠PBD=67.5°-45°=22.5°,
∴∠DPB=∠DBP,
∴DP=DB,
在Rt△BDE中,BE=DE=2,由勾股定理可得,BD=22,
∴PE=2+22,
∴P(1,2+22);
当点P在x轴下方时,由对称性可知P点坐标为(1,-2-
22),
综上可知,抛物线的对称轴上存在点P,使∠APB=∠ABC,P
点坐标为(1,2+22)或(1,-2-22);
(3)如解图②,作点A关于y轴对称的点F,
点F的坐标为(1,0),
则∠OCA=∠OCF,
设直线CF的解析式为y=kx+b,
把点C(0,3),F(1,0)代入求得k=-3,b=3,
则直线CF的解析式为y=-3x+3,
y=-3x+3
联立y=-x2+2x+3,
x1=0
解得y1=3,
x2=5
y2=-12,
直线CF与抛物线的交点坐标为
(0,3)、(5,-12),第1题解图②设点Q的坐标为
(a,-a2+2a+3),
当0<a<5时,∠OCF<∠OCQ,则∠OCA<∠OCQ;
当a=5时,∠OCF=∠OCQ,则∠OCA=∠OCQ;
当a>5时,∠OCF>∠OCQ,则∠OCA>∠OCQ.
类型二线段及周长问题
★1.如图,抛物线y=-14x2+bx+c的图象过点A(4,0),
B(-4,-4),且抛物线与y轴交于点C,连接AB,BC,AC.
(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的点,求△PBC周长的最小值及此
时点P的坐标;
(3)若E是线段AB上的一个动点(不与A、B重合),过E作y轴的平行线,分别交抛物线及x轴于F、D两点.请问是否存
在这样的点E,使DE=2DF?
若存在,请求出点E的坐标;若不存在,请说明理由.
第1题图
解:
(1)∵抛物线y=-14x2+bx+c的图象经过点A(4,0),B(-4,-4),
-
1
164bc0
1
4
b
,
2
∴
1
,解得
-
164bc4
c2
4
∴抛物线的解析式为y=-14x2+12x+2;
(2)由抛物线y=-14x2+12x+2可得其对称轴为直线x=
1
2
-1=1,点C的坐标为(0,2),
2(-4)
如解图,作点C关于对称轴x=1的点C′,则C′的坐标为(2,2),连接
BC’;
即BC′=(24)2(24)2=62,
BC′与对称轴的交点即为所求点P,连第1题解图
接CP,
此时△PBC的周长最小.
设直线BC′的解析式为y=kx+m,
∵点B(-4,-4),C′(2,2),
∴2km2
,解得k1
,
4km4
m0
∴直线BC′的解析式为y=x,
将x=1代入y=x,得y=1,
∴点P坐标为(1,1).
∴BC=42(24)2213.
∵△PBC的周长为CP+BC+PB=BC+BC′,
∴△PBC周长的最小值为213+62;
(3)由点A(4,0),B(-4,-4)可得直线AB的解析式为y=12x-2,设点E(x,12x-2),其中-4F(x,-14x2+12x+2),DE=|12x-2|=2-12x,DF=|-14x2+12x+2|,
当2-12x=-12x2+x+4,即点F位于x轴上方,解得x1=-1,x2=4(舍去),
将x=-1代入y=
1
x-2,得到y=-
5
,∴E(-1,-
5
),
2
2
2
当2-12x=12x2-x-4,即点F位于x轴下方,
解得x1=-3,x2=4(舍去),将x=-3代入y=12x-2,得到y=-72,∴E(-3,-72).
综上所述:
点E的坐标为:
(-1,-52),(-3,-72).
★2.如图,在平面直角坐标系中,点O为坐标原点,直线y=-x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=-x+4交于另一点B,且点B的横坐标为1.
(1)求抛物线的解析式;
(2)点P是线段AB上一个动点(点P不与点A、B重合),过点
P作PM∥OB交第一象限内的抛物线于点M,过点M作
MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,
设PF的长为t,
①求MN与t之间的函数关系式(不要求写出自变量t的取值
范围);
②当MN取最大值时,连接ON,直接写出sin∠BON的值.
第2题图
解:
(1)∵y=-x+4与x轴交于点A,
∴A(4,0),
∵点B的横坐标为1,且直线y=-x+4经过点B,∴B(1,3),
∵抛物线y=ax2+bx经过A(4,0),B(1,3),
16a4b0
,
∴
3
ab
a1
解得.
b4
∴抛物线的解析式为y=-x2+4x;
(2)①如解图①,作BD⊥x轴于点D,延长MP交x轴于点E,
第2
∵B(1,3),A(4,0),
∴OD=1,BD=3,OA=4,
∴AD=3,
∴AD=BD,
∵∠BDA=90°,∴∠BAD=∠ABD=45°,
∵MC⊥x轴,
∴∠ANC=∠BAD=45°,
∴∠PNF=∠ANC=45°,
∵PF⊥MC,
∴∠FPN=∠PNF=45°,
∴NF=PF=t,
∵∠PFM=∠ECM=90°,
第2题解图①
∴PF∥EC,
∴∠MPF=∠MEC,
∵ME∥OB,
∴∠MEC=∠BOD,
∴∠MPF=∠BOD,
∴tan∠BOD=tan∠MPF,
∴ODBD=MFPF=3,
∴MF=3PF=3t,
∵MN=MF+FN,
∴MN=3t+t=4t;
②如解图②,作BG⊥ON于G点,
第2题解图②
当过点M的直线与直线AB平行且与抛物线只有一个交点时,MN取最大,
∴设与AB平行的直线y=-x+b,
当-x2+4x=-x+b;即x2-5x+b=0,
25
=25-4b=0,解b=4.
25
∴直线y=-x+4,
∴抛物线y=-x2+4x与y=-x+254的交点M(52,154),
∴N点的横坐标为52,N点的纵坐标为-52+4=32,即N(52,
32),
∴ON的解析式为y=53x,
∵BG⊥ON,
5
设BG的解析式为y=-3x+b,
将B(1,3)代入y=-
5
x+b,解得b=
14
,
3
3
514
∴BG的解析式为y=-3x+3,
y
3
x
x
35
5
17
联立
5
14,解得
21,
y
x
y
3
3
17
3521
即G(17,17).
∴由勾股定理,得OB=1232=10,
BG=(17351)2(17213)2=61734,
634
∴sin∠BON=BG=17=685.
OB1085
★3如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),
交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)在抛物线对称轴上是否存在点M,使|MA-MC|最大?
若
存在,请求出点M的坐标,若不存在,请说明理由.
解:
(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
93bc0
b-4
,
∴
,解得
1bc0
c3
∴抛物线解析式为y=x2-4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=-x+3,
设点P(x,x2-4x+3),
∵PD∥y轴,
∴点D(x,-x+3),
39
∴PD=(-x+3)-(x2-4x+3)=-x2+3x=-(x-2)2+4,∵a=-1<0,
∴当x=32时,线段PD的长度有最大值94;
(3)由抛物线的对称性,对称轴垂直平分AB,
∴MA=MB,
由三角形的三边关系,|MA-MC|∴当M、B、C三点共线时,|MA-MC|最大,即为BC的长
度,
设直线BC的解析式为y=kx+m(k≠0),
km0
k3
,
则
,解得
m3
m3
∴直线BC的解析式为y=-3x+3,
∵抛物线y=x2-4x+3的对称轴为直线x=2,
∴当x=2时,y=-3×2+3=-3,
∴点M(2,-3),
即抛物线对称轴上存在点M(2,-3),使|MA-MC|最大.类型三面积问题
★1.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,
4).
(1)求此抛物线的解析式;