初等代数研究课后习题答案完整版余元希Word下载.docx
《初等代数研究课后习题答案完整版余元希Word下载.docx》由会员分享,可在线阅读,更多相关《初等代数研究课后习题答案完整版余元希Word下载.docx(11页珍藏版)》请在冰豆网上搜索。
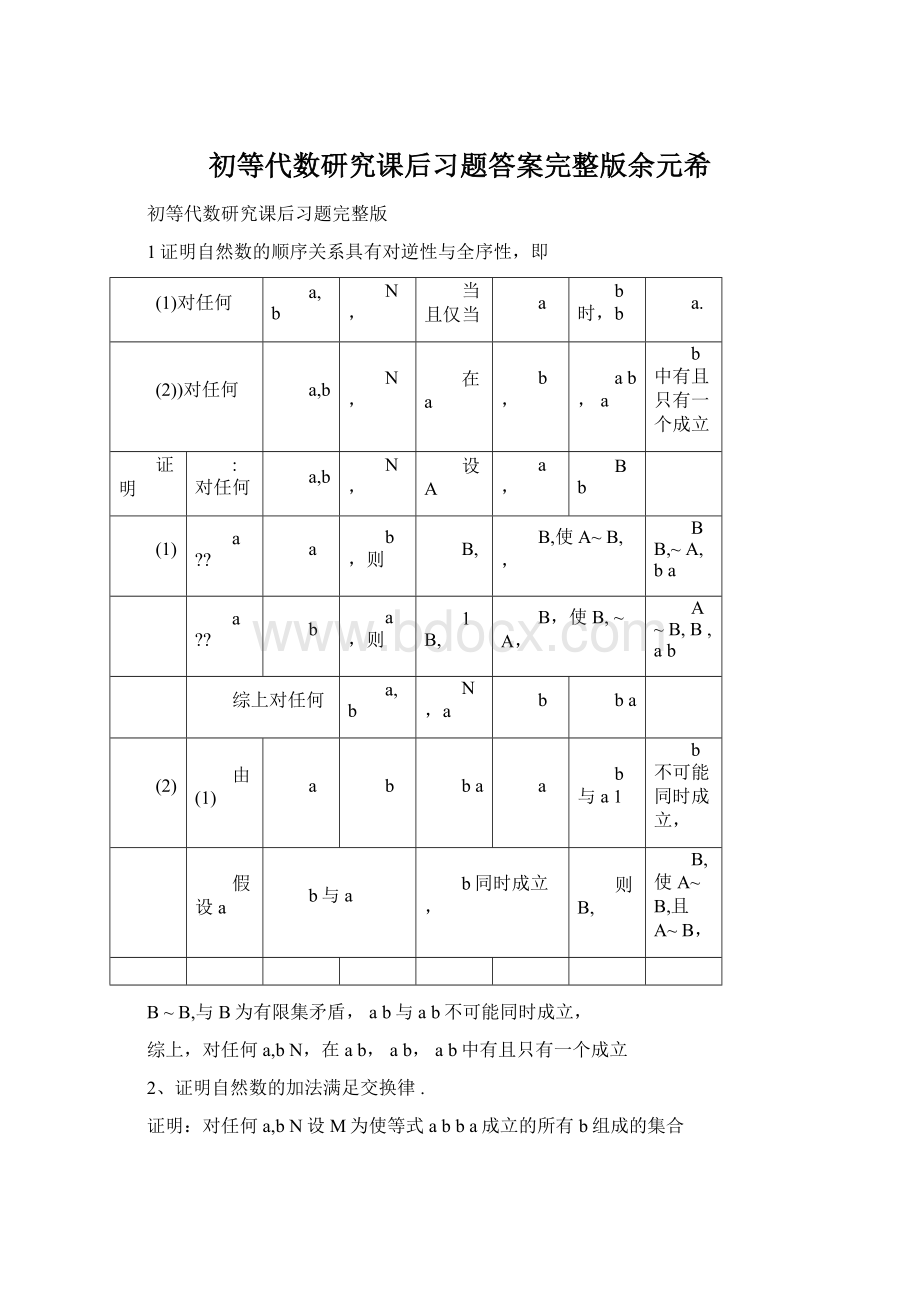
N,a
ba
(2)
由
(1)
b与a1
b不可能同时成立,
假设a
b与a
b同时成立,
则B,
B,使A~B,且A~B,
B~B,与B为有限集矛盾,ab与ab不可能同时成立,
综上,对任何a,bN,在ab,ab,ab中有且只有一个成立
2、证明自然数的加法满足交换律.
证明:
对任何a,bN设M为使等式abba成立的所有b组成的集合
先证a
11
设满足此式的
a组成集合
k,
显然有1+1=1+1成立
1k
,设
k,a11
a1
(a
)(a1)
(1a)
1
ak,
k
取定a,则
1M,
设
M,abba,则
ab(a
b)
(b
a)ba
bM
J
M
N
abba
3、证明自然数的乘法是唯一存在的
唯一性:
取定a,反证:
假设至少有两个对应关系f,g,对bN,有
f(b),g(b)N,设M是由使f(b)g(b)成立的所有的b组成的集合,
f(b)g(b)a11M设bN则f(b)g(b)f(b)ag(b)a
f(b)g(b),bM,MN即bN,f(b)g(b)
1,1b
1b11
k,设aK,
有a,l
b与它对
应
且1
a,abab
a,对bN,令a
abb
ab
ab
b1
(ab
1)
K
即乘法存在
乘法是唯一的
存在性:
设乘法存在的所有a组成集合K当a1时,bN,
p24—5、解:
满足条件的
A有A
{1,2},A2{1,2,3},A3{1,2,4},A{1,2,5}
A2,A2
A3A4
3,As
A
A7
4,A
5基数和为2
3343528
p24—6、证明:
Aa,B
A中的x与B中的
y对应
Bab,
B
Aba
AB
p24—&
1)3+4=7
31
343
231
(31)4
5
33
32
(3
2)
6
34
3)
7
2)34
12
3
36
9
p24—12、证明:
1)(m
n)
m
n
A5
(mn)
mn1(m1)n
2)(mn)nmm
(mn)mn1mn(m1)nmm
p26—36、已知f(m,n)对任何m,nN满足
f(1,n)n1
f(m1,1)f(m,2)
f(m
1,n1)
f(m,f(m1,n))
求证:
f(2,n)
n2
f(3,n)
2n2
f(4,n)
2n12
1)当n1时,f(2,1)f(11,1)f(1,2)2112结论成立,
假设nk时,结论成立,即f(2,k)k2,
当nk1时,
f(2,k1)f(11,k1)f(1,f(2,k))
f(1,k2)(k2)1(k1)2
所以对一切自然数结论都成立
2)当n1时,f(3,n)f(21,n)f(2,2)22212结论成立
假设nk时,结论成立,即f(3,k)2k2
f(3,k1)f(21,k1)f(2,f(3,k))
f(2,2k2)2k222(k1)2
3)当n1时,f(4,1)f(31,1)f(3,2)2222112结论成立
假设nk时,结论成立,即f(4,k)2k12
f(4,k1)f(3,f(4,k))f(3,2k12)
2(2k12)22k22
p62—1、证明定理2.1
[a,b],[c,d]Z,[a,b][c,d][ac,bd]
因为自然数加法满足交换律[ac,bd][ca,db]
而[c,d][a,b][ca,db][a,b][c,d][c,d][a,b]
“”已知[a,b][c,d]则adbc
p62—5、已知[a,b],[c,d]Z,求证([a,b][c,d])[a,b][c,d]
左边([a,b][c,d])[ad,bc][bc,ad]
右边[a,b][c,d][b,a][c,d][bc,ad]
所以左边等于右边([a,b][c,d])[a,b][c,d]
p62—7、已知a,b,cN,求证当且仅当adbc时[a,b][c,d]
“”已知adbc,[a,b][c,d][ad,bc]
因为adbc[ad,bc]是负数,[a,b][c,d]
已知[a,b][c,d]则[a,b][c,d][ad,bc]
因为[ad,bc]是负数,adbc
设[a,b],[c,d]
而ab,cd
(ac)(bd)(ab)(cd)ab
[acbd,ad
bc]
acbd(adbc)
而
cd
acbd
(adt
)c)
a(c
d)
b(d
c)(ab)(cd)
abcd
II
k名胜负的次数各为ak,bk,
p63—12、n名棋手每两个比赛一次,没有平局,若第
、22222
k1,2,,n,求证:
aia2...anbib2
对于ak(k1,2,...,n),必存在一个bj(j1,2,...,n)使得akbj
b10aps,d10cpt
adbc10acapt(10accps)p(csat)padbc
p63—17、设2不整除a,求证8a21
p63—20、设aZ,求证a(a1)(a2)(a3)1是奇数的平方
(a1)(a2)肯定为偶数
a(a
1)(a
2)(a3)1
[(a
1](a1)[(a2)(a2)1]1
1)2
(a1)][(a
2)2
2)]1
1)2(a
2)22(a
2)1]2
a1,a2肯定一奇一偶
(a1)(a2)1肯定为奇数
p63—22、证明:
前n个自然数之和的个位数码不能是2、4、7、9
前n个自然数的和为°
n)n
2
因为:
n个自然数的和仍为自然数1+n与n中必定一个为奇数一个为偶数
若个位数码为2
则1+n与n的个位数码只能是1,4或4,1
而(1+n)-n=1个位数码不能为2
若个位数码为4
则1+n与n的个位数码只能是1,8或8,1也不可能成立若个位数码为7
则1+n与n的个位数码有2种可能,则2,7或1,14
也不可能成立,若个位数码为9
则1+n与n的个位数码有2种可能,即2,9或1,18也不可能成立,
综上,前n个自然数和的个位数码不能是2,4,7,9
p63—26、证明2.3定理1(a1,a2,……a.,)=(a1,a2,……an)
(a1,a2,……a“)是印^,……an的公因数中的最大数
所以R需考虑非负整数(a1,a2,an,)=(a1,a2,an)
p63—29、证明2.3定理4的推论(a,b)1的充要条件是有x,yZ使得axby1
因为(a,b)1
a,b不全为0
“”由定理4
x,yZ使axby(a,b)1
“”设(a,b)
d则da,db,daxbyd1d(a,b)1
p63—30、证明2.3定理6及其推论。
定理6:
若mN,贝U(ma,mb)m(a,b)
若a,b都为0,则(0,0)m(0,0)显然成立
若a,b不全为零,则X0,y°
Z使ax°
by。
(a,b)
IIIIII
maxmby(ma,mb)而maxmbym(axby)
因为x,yZ,ax0by°
axbyax0by。
axby
m(ax0by0)maxmbym(a,b)maxmbym(a,b)(ma,mb)
而(ma,mb)amx^mby0m(a,b)(ma,mb)m(a,b)
推论:
设d是a,b的公因数,贝U(a/d,b/d)1的充要条件是d(a,b)
“”d是a,b的公因数dNdd(a/d,b/d)(a,b)
“”因为d(a,b)x,yZ,使axbyd
x,yZ,使(a/d)x(b/d)y1(a/d,b/d)1
p64—32、证明2.3定理七及其推论
定理七:
若(a,c)1,bZ,b,c中至少有一个不为0,则(ab,c)(b,c)
b,c中至少有一个不为0x,yZ使abxcy(ab,c)
因为(a,c)1(ab,c)b,(ab,c)c因为(b,c)(ab,c)(ab,c)(b,c)
若(a,c)1,(b,c)1,则(ab,c)1
因为(b,c)1,b,c不为零(ab,c)(b,c)1
p64—33、已知n是奇数,nab,nab,求证n(a,b)
因为nab,nabn(ab)(ab),n(ab)(ab)
n2a,n2bn2(a,b),因为n是奇数,n(a,b)
p64—36、已知(a,b)d,(a,b)d,求证(aa,ab,ab,bb)dd
(aa'
ab'
)a(a'
b'
)ad'
(a'
b,bb'
)bd'
IIIIIII
(aa,ab,ab,bb)(ad,bd)dd
p64—40、已知aN,求证a,2a,……na中n的倍数的个数等于(n,a)
当(n,a)d时,d1,令adai,(n,aj1,则a,2a,na可改写为
da1,2da1,nda1因为d1所以其中一定包括na1,2na^(d1)na^dna1
都是n的倍数,共有d个
p64—42、已知p是异于3的奇素数,求证24p1
p是异于3的奇素数,p21为偶数,p3p219
p1(p1)(p1)其中p1,p1都为合数,且都大于3
p1,p1都可被2、3中的一个整除,若2p1,则由p1(p1)2
2p1,因为p13,p1324p21
p64—44、已知整数a,n都大于1,an1是素数,求证a2且n是素数
反证n不是素数当a2时an1不是素数与已知矛盾,所以n是素数
p64—45、求不大于50的一切素数
解:
平方不大于50的素数是2,3,5,7则不大于50的一切素数
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47
p64—46、求下列各数的标准分解式:
1)82798848
82798848=2835113
p64—49、已知整数a,b,c都大于1,求证[(a,c),(b,c)]([a,b],c)
1)因为(1,p)1,(2,p)1,...,(p1,p)1
1p1(modp),2p2(modp),3p3(modp)…(p1)pp1(modp)
12p3p...(p1)p(123...(p1))(modp)
12p3p...(p1)pO(modp)
2)1p11(modp),2p11(modp),3p11(modp)…(p1)p11(modp)
12p13p1...(p1)p11(modp)
q1p1
p66—70、设p,q是相异素数,求证pqqp1(modpq)
pq10(modp),qp11(modp),pq1qp11(modp)
同理pq1qp11(modq)pq1qp11(mod[p,q])
即pq1qp11(modpq)
p66—72、已知p是素数,N,求证
(1)(p)(p2)...(p)p
因为p是素数,所以(pk)pkpk1,kN
221
(p)p1,(p)pp,....,(p)pp
因为
(1)1
(1)(p)(p2)...(p)p
p66—73、计算(66150)
322
66150的标准分解式为661502357
02
(66150)2357(21)(31)(51)(71)15120
p66—74、已知整数a2,求证2(a)
设a的标准分解式为aP11P22...Pnn,其中P1,P2,...,Pn为素数
i1,(i1,2,...,n),若a2n显然(a)2a2a1,2(a)
当a2n时,一定p12且p-i1为偶数,2(a)
综上所述a2时2
(a)