计算方法课后题文档格式.docx
《计算方法课后题文档格式.docx》由会员分享,可在线阅读,更多相关《计算方法课后题文档格式.docx(29页珍藏版)》请在冰豆网上搜索。
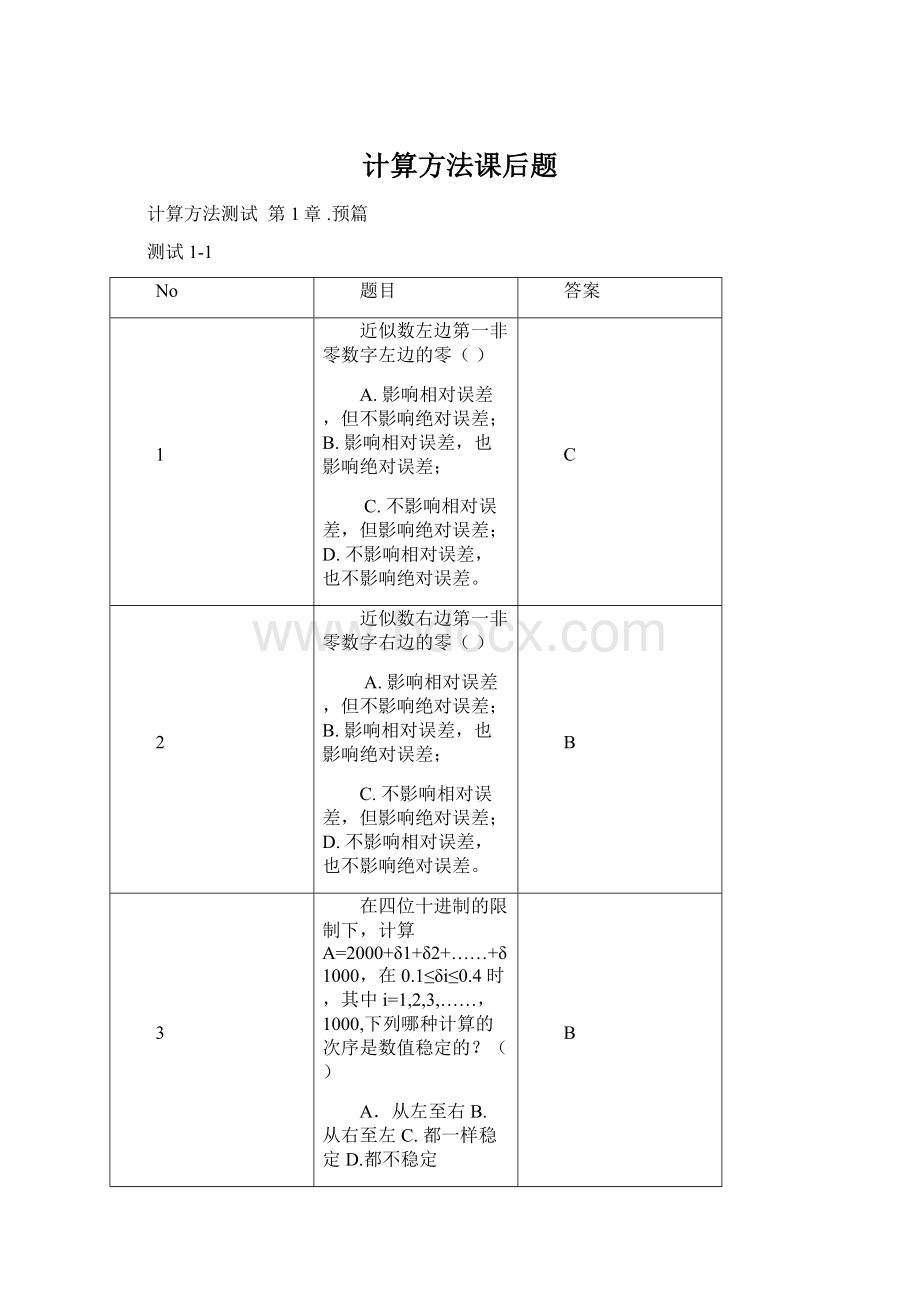
近似数的四则运算法则有()
A.ε(x+y)=ε(x)+ε(y)B.ε(x×
y)=ε(x)+ε(y)
C.δ(x+y)=δ(x)+δ(y)D.δ(x×
y)=δ(x)+δ(y)
AD
9
取x=1.4142,具有三位有效数字的近似值为()
1.42
10
已知近似数285.35,186.87,58.43,4.96都准确到末位数字
求这些近似数之和
若舍入成535.6,则绝对误差的保守估计为()
0.03
11
四舍五入得到的近似数999.8,其绝对误差为0.5×
10-1,相对误差为0.5001×
10-5,所以有效数字为五位。
(),
F
12
把无限的计算过程用有限的计算过程代替,这样产生的误差叫截断误差。
T
13
计算过程中,误差的指数增长,这时认为算法是数值是数值稳定的,从而计算的结果是可以接受的。
14
相对误差,通常写成百分数的形式,所以又称百分误差。
15
为简单计,人们常把绝对误差限说成是绝对误差。
测试1-2
完备的内积空间叫做()空间。
A.BanachB.HilbertC.Cauchy-SchwarzD.Euler-Schwarz
完备的线性赋范空间叫做()空间。
A
设(x,y)为实线性空间V上内积,x,y∈V,则有(x,y)2≤(x,x)(y,y)
称为()不等式。
A.BanachB.HilbertC.Cauchy-SchwarzD.Euler-Schwarz
在Cm×
n中,对任一个矩阵A,实数‖A‖是矩阵A的范数的四个条件如下,表达不正确的是()
A.‖A‖≥0,且‖A‖=0A=0B.‖kA‖=|k|.‖A‖
C.‖A+B‖≤‖A‖+‖B‖D.‖A.B‖=‖A‖.‖B‖
下列命题正确的有:
A.两个上三角阵的积为上三角阵。
B.下三角阵的逆为上三角阵
C.λ是A的特征值,则λ是AT的特征值
D.A为对称正定阵,当满足xTAx>
0,∀x≠0
ACD
A.实对称阵A的特征值都是实数
B.对应于实对称阵A不同特征值的特征向量必正交
C.n阶实对称阵A有n个线性无关的特征向量
D.如果A是实对称阵,则存在正交阵P,使
P-1AP=PTAP为对角阵
ABCD
X=(1,-2,3,-4),则x的1-范数‖x‖1=();
2-范数为();
∞-范数为();
如果
,则A的1-范数为();
如果
则B的F-范数为();
测试2-1
使用Gauss消去法求解一个n元线性方程组Ax=b所需乘(除法)运算次数约为:
A.ln(n)/3B.n/3C.n3/3D.10n/3
Gauss消去法第k次消元()
A.aij(k)=aij(k-1)-lik×
akj(k-1)(i=k+1,……,n;
j=i,……,n)
B.aij(k)=aij(k-1)-lik×
akj(k-1)(j=k+1,……,n;
i=j,……,n)
C.aij(k)=aij(k-1)-lik×
j=k+1,……,n)
D.aij(k)=aij(k-1)-lik×
akj(k-1)(i=1,……,n;
Gauss消去法第k次消元,是用()
A.第k列元素去消后面的n-k列元素B.第k列元素去消后面的n-k行元素
C.第k行元素去消后面的n-k列元素D.第k行元素去消后面的n-k行元素
Gauss列主元素法第k次消元,列主元素,是():
A.第k行中绝对值最大的元素。
B.第k行,从第k列到第n列中绝对值最大的元素。
C.第k列中绝对值最大的元素。
D.第k列,从第k行到第n行中绝对值最大的元素。
Gauss消去法失败,则()
A.系数矩阵A能进行三角分解B.系数矩阵A不能进行三角分解
C.如果系数矩阵A非奇异,能进行三角分解D.如果系数矩阵A奇异,能进行三角分解
三角分解法算法优点()
A.比Gauss消去法误差小B.适用于系数矩阵A是大型稀疏矩阵
C.比Gauss消去法速度快D.当Gauss消去法失败时,仍然有解
AB
对于n元线性方程组Ax=b,LU分解表示:
A.系数矩阵A一定可以进行LU分解
B.如果系数矩阵A可以进行LU分解,则分解是唯一的
C.如果Gauss消去法有解,则A可以进行LU分解
D.如果Gauss列主元法有解,则A可以进行LU分解
BC
与Gauss消去法比较,列主元素法的优点:
A.速度快B.如果方程有解,则算法一定有解。
C.算法稳定性好D.如果系数矩阵A非奇异,则算法一定有解。
CD
Doolittle分解有许多优点
A.计算没有浪费,所以又称它为“紧凑消元法”;
B.乘法计算量大大小于Gauss消去法;
C.重复使用内存单元,可节省内存
D.若使用“双倍位累加器”计算,并作最后一次舍入,可提高解的的精度;
如果A矩阵(),则A可作LU分解,且这种分解是唯一的。
A.为严格对角占优阵;
B.为不可约弱对角占优阵;
C.为对称矩阵;
D.为正定矩阵。
下列说法正确的是()
A.Gauss消去法有解,则Gauss列主元素法有解。
B.Gauss列主元法比Gauss消去法速度快。
C.如果一个矩阵能进行LU分解,则LU分解是唯一的。
D.A对称正定,则A可作LU分解,且这种分解是唯一的。
计算填空
线性方程组
系数矩阵A=(),其行列式det(A)=()增广矩阵为(),
进行LU分解,L=(),U=()方程组解为X=()
第3章线性方程组迭代解法
测试3-1
对于线性方程组AX=b,如果写成一般迭代公式X(k+1)=BX(k)+f,那么Jacobi迭代公式中的B的表达式()
A.B=D-1(L+U)B.B=D-1(L-U)C.B=(L-U)D-1D.B=(L+U)D-1
对于线性方程组AX=b,如果写成一般迭代公式X(k+1)=BX(k)+f,那么Jacobi迭代公式中的f的表达式():
A.f=D-1bB.f=(D-L)-1bC.f=bD-1D.f=b(D-L)-1
对于线性方程组AX=b,迭代公式X(k+1)=BX(k)+f,那么Gauss-Seidel迭代公式中()
A.B=(D+L)-1UB.B=(D-L)-1UC.B=D-1U-L-1UD.B=D-1U+L-1U
对于线性方程组AX=b,迭代公式X(k+1)=BX(k)+f,那么Gauss-Seidel迭代公式中()
A.f=(D+L)-1bB.f=(D-L)-1bC.f=b(D+L)-1D.f=b(D-L)-1
对于线性方程组AX=b的迭代公式X(k+1)=BX(k)+f,如果谱半径(),则迭代收敛。
A.ρ(B)>
1/2B.ρ(B)>
1C.ρ(B)<
1D.ρ(B)=1
对于线性方程组AX=b的迭代公式X(k+1)=BX(k)+f,如果收敛,则矩阵B范数()
A.‖B‖<
1B.‖B‖>
1C.‖B‖≤1D.取值不一定
求解线性方程组Ax=b的数值算法直接法主要有:
A.Gauss-Seidel迭代法B.Jacobi迭代法C.三角分解法D.列主元法
对于线性方程组AX=b的迭代公式X(k+1)=BX(k)+f,迭代是否收敛()。
A.与A无关B.与B无关C.与迭代初值无关D.与f无关.
A.Jacobi迭代是否收敛与迭代初值无关。
B.Jacobi迭代收敛,则Gauss-Seidel迭代一定收敛。
C.迭代公式x(k+1)=Bx(k)+f(k=0,1,2,...)收敛,则矩阵B的谱半径ρ(B)≤1
D.矩阵B的谱半径ρ(B)≤1,则迭代公式x(k+1)=Bx(k)+f(k=0,1,2,...)收敛
方程组Ax=b中,如果A矩阵()条件下,Jacobi迭代法和Gauss-Seidel迭代法均收敛。
A.为严格对角占优阵;
对于线性方程组AX=b的迭代公式X(k+1)=BX(k)+f,如果(),迭代收敛。
A.‖B‖1<
1B.‖B‖1≤1C.‖B‖2<
1D.‖B‖2≤1
计算填空线性方程组AX=b
①Jacobi迭代矩阵为()
②Jacobi迭代(收敛/不收敛),因为()
③取初值x0=(0.0000,0.0000,0.0000,0.0000),计算Jacobi迭代x1=()
④取初值x0=(0.0000,0.0000,0.0000,0.0000),计算Gauss-Seidel迭代x1=()
收敛
对角占优
第4章.插值方法
测试4-1
1.
已知Pn(x)是Lagrange插值多项式,则P2(x)的正确表达方式是:
P2(x)=()
A.
B.
C.
D.A+B+C
通过四个点(xi,yi)(i=0,1,2,3)的插值多项式是()的多项式.
A.二次;
B.三次;
C.四次;
D.不超过三次.
3.
f(x)=2x2+3x+1的Lagrange插值多项式p4(x)是()次多项式。
A.1B.2C.3D.4
4.
插值是()等数值方法的基础,是重要的数学工具。
A.线性方程组B.函数逼近C.数值积分D.微分方程
5.
Lagrange插值基函数()。
A.与节点无关B.与节点顺序无关
C.与节点的函数值无关D.与节点的函数值顺序无关
6.
A.Lagrange插值多项式pn(x)是n次多项式。
B.Lagrange插值多项式具有直观、对称、容易编程上机等优点。
C.如果f(x)不连续,则其插值多项式可能不存在。
D.如果f(x)不连续,则其插值多项式可能不唯一。
7.
填空
Lagrange插值多项式Pn(x)基函数的正确表达式为()
Lagrange插值余项的表达式正确的为:
已知数据表为函数y=f(x)在3个节点上的函数值(如下表),求Lagrange插值多项式
P2(x)=(),并求f(0.6)的近似值
已知数据表为函数y=f(x)在4个节点上的函数值(如下表),求Lagrange插值多项式
P3(x)=()
f(x)=2x2-1
x
0.0
0.2
0.4
0.6
0.8
y
-1.000
-0.92
-0.68
-0.28
0.28
.
测试4-2
n次多项式
的K阶均差p[x,x1,x2,…,xk],当k≤n时,是()多项式
A.k次B.n-k次C.n次D.无法确定是多少次
2.
Newton插值法与Lagrange插值法比较,每增加一个结点,则()
A.Newton插值多项式与Lagrange插值多项式的所有系数都得重算
B.Newton插值多项式与Lagrange插值多项式都只需增加计算一项新系数
C.Newton插值多项只需增加计算一项新系数;
D.Lagrange插值多项式只需增加计算一项新系数。
f(x)在xi,处的2阶向前差分表达式正确的有()
A.
B.
C.
D.
4.
已知函数yi=f(xi)(i=0,1,2,…,n),要求估计f(z)(a<
z<
b)的值,则可以考虑的方法有()
A.Euler法;
B.Newton插值法;
C.Jacobi迭代法;
D.Lagrange插值法。
BD
5.
的K阶均差p[x,x1,x2,…,xk]
A.与节点顺序无关B.是关于x的多项式
C.与节点的函数值无关D.是节点函数值的线性组合
ABD
A.f(x)=2x2+3x+1的1阶均差一定是非负的。
B.f(x)=2x2+3x+1的2阶均差一定是非负的。
C.f(x)=2x2+3x+1的3阶均差一定是非负的。
D.n次多项式的n-1阶差分为常数。
f(x)关于xi,xi+1的一阶均差表达式是()
已知数据表为函数y=f(x)在5个节点上的函数值,则均差
f[x0,x1]=(),f[x0,x1,x2]=(),f[x0,x1,x2,x3]=(),f[x0,x1,x2,x3,x4]=()
填空已知数据表为函数y=f(x)在5个节点上的函数值,则
Newton插值多项式N4(x)=(),可估算f(0.3)≈.
Lagrange插值多项式P3(x)=()
已知数据表为函数y=f(x)在5个节点上的函数值y=2x3+3x2-1
-0.864
-0.392
0.512
1.944
第5章数值积分
测试5-1
变步长梯形求积公式为
A.
B.
C.
D.
变步长Simpson求积公式为()
A.
B.
C.
变步长Simpson求积公式Sk中的k表示将积分区间分成()等份
A.kB.2k-1C.2kD.2k-1
下列说法错误的是()
A.梯形规则的几何意义是:
用经过(x0,f0)和(x1,f1)两点的直线下面的阴影部分的梯形的面积近似代替f(x)下面的曲边梯形的面积。
B.变步长梯形求积公式Tk中,将积分区间分成k等份。
C.Simpson公式的节点必须是等距的。
D.变步长梯形求积公式较复合梯形求积公式更适合计算机计算。
复合梯形求积公式具有
(1)阶代数精度。
变步长梯形求积公式具有
(1)阶代数精度。
Simpson求积公式具有(3)阶代数精度。
如果f(x)=3x2+1,利用定积分知识可以计算f(x)在[0,1]区间积分值=2。
如果f(x)=3x2+1,则可计算[0,1]区间变步长梯形积分值T0=2.5;
T1=2.125;
T2=2.03125。
如果f(x)=3x2+1,则可计算[0,1]区间变步长Simpson积分值S1=2;
S2=2。
2.5,2.125,2.03125
2,2
f(x)=3x2+1,F(x)=x3+x;
0.25
0.5
0.75
f
1.1875
1.75
2.6875
测试5-2
Cotes系数与()无关
A.插值节点的位置iB.积分区间
C.构造插值多项式插值节点的个数nD.被积函数
()求积公式代数精度是1阶的。
A.梯形B.复合梯形C.SimpsonD.变步长Simpson
对函数f(x)=(),Simpson求积公式是准确的。
A.x+1B.x2+x+1C.x2+1D.x3+1
A.数值积分正是Newton-Leibniz公式用于计算机数值计算的理论基础。
B.Simpson规则的几何意义是:
用经过(x0,f0)和(x2,f2)两点的直线下面的阴影部分的梯形的面积近似代替f(x)下面的曲边梯形的面积。
C.变步长Simpson求积公式中,Sk表示具有k阶代数精度。
D.Romberg算法
,在计算过程中,一般是逐列计算的。
求积公式Cotes规则有()阶代数精度。
NC积分公式中,若n为奇数,则其代数精度是(n)阶;
若n为偶数,则其代数精度是(n+1)阶。
如果f(x)计算[0,1]区间上变步长梯形积分值T0(0)=0.7500;
T0
(1)=0.6250;
T0
(2)=0.6554;
T0(3)=0.6735;
则可利用Romberg算法,可求得第二列积分值,该列即数值积分Simpson公式。
第二列积分值T1
(1)=0.5833,T1
(2)=0.6655;
T1(3)=0.6795.
利用Romberg算法,可求得第三列积分值T2
(1)=0.6639,T2
(2)=0.6804.
该列即数值积分Cotes规则公式。
利用Romberg算法,可求得第四列积分值T3
(1)=0.6807.
该列即数值积分Romberg公式。
n,n+1
Simpson
Cotes规则
Romberg
注f(x)=1/(x+1),F(x)=ln(x+1),F
(1)=0,F
(2)=0.69314718055994530941723212145818
0.125
0.375
0.625
0.875
1.0
0.8888
0.7272
0.6667
0.6154
0.5714
0.5333
T0
0.6554
0.6735
T1
0.5833
0.6655
0.6795
T2
0.6639
0.6804
T3
0.6807
第7章.常微方程初值问题数值解法
测试7-1
常微分方程数值方法中,如果某种方法的截断误差为O(hp+1),则称该方法具有()阶精度。
A.p-1B.pC.p+1D.h
常微分方程数值方法中,yn+1=yn+hf(xn,yn),则称该方法为()
A.Euler公式B.改进Euler公式
C.梯形公式D.一次校正法
常微分方程Euler公式的截断误差为()
C.
D.
常