北师大版学年七年级数学下册期末测试题及答案文档格式.docx
《北师大版学年七年级数学下册期末测试题及答案文档格式.docx》由会员分享,可在线阅读,更多相关《北师大版学年七年级数学下册期末测试题及答案文档格式.docx(28页珍藏版)》请在冰豆网上搜索。
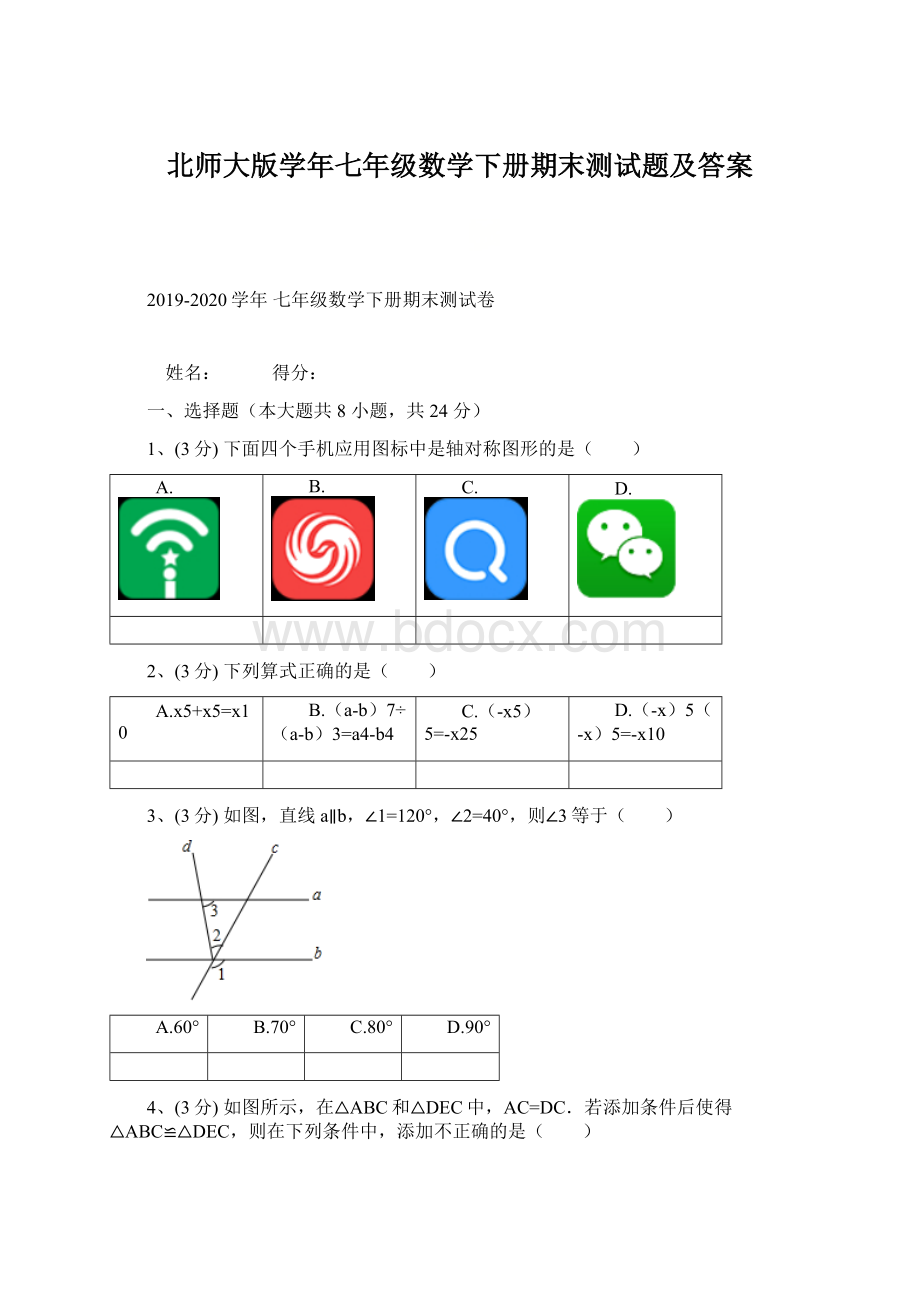
B.a+2b
C.2a+b
D.2a+2b
二、填空题(本大题共8小题,共24分)
9、(3分)水珠不断滴在一块石头上,经过若干年,石头上形成了一个深为0.0000048cm的小洞,则数字0.0000048用科学记数法可表示______.
10、(3分)
=______.
11、(3分)任意写出一个两位数,个位上的数字恰好是5的概率的是______.
12、(3分)一张纸条如图所示,BC∥DE,将纸条沿着BE折叠,若∠ABC=38°
,则∠DEF的度数是______.
13、(3分)已知,一副三角板如图所示摆放,此时∠ABC=35°
,那么∠DEF=______.
14、(3分)如图所示,DE、FG分别是△ABC两边AB、AC的中垂线,分别交BC于E、G.若BC=12,EG=2,则△AEG的周长是______.
15、(3分)已知整数a1,a2,a3,a4,…满足下列条件:
a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…依此类推,则a2017的值为______.
16、(3分)已知,等腰△ABC中,AB=AC,E是高D上任一点,F是腰AB上任一点,腰AC=5,BD=3,AD=4,那么线段BE+EF的最小值是______.
三、解答题(本大题共6小题,共44分)
17、(4分)已知线段a和∠1,
求作:
等腰△ABC,使腰AB=AC=2a,底角等于∠1.
18、(6分)推理填空
已知,如图,AB∥CD,AD∥BC,BE平分∠ABC交AD于E,DF平分∠ADC交BC于F,求证:
BE∥DF.
证明:
∵AD∥BC
∴∠A+______=180°
(两直线平行,同旁内角互补)
∵AB∥CD
∴______=______(______)
又∵BE平分∠ABC
∴______=
∠ABC(角平分线定义)
又∵DF平分∠ADC
∠ADC(角平分线定义)
∴______=______
∴∠AEB=______(两直线平行,内错角相等)
∴______=______(等量代换)
∴BE∥DP(同位角相等,两直线平行)
19、(6分)小明和小丽做游戏:
一只蚂蚁在如图所示的方格纸上爬来爬去,并随意停留在某处,若蚂蚁停留在阴影区域,小明胜,否则小丽胜.这个游戏对双方公平吗?
请说明理由.
20、(8分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16min时到家,假设小东始终以100m/min的速度步行,两人离家的距离y(单位:
m)与小东打完电话后的步行时间t(单位;
min)之间的函数关系如图所示:
(1)小东打电话时,他离家______m;
(2)填上图中空格相应的数据______;
(3)小东和妈妈相遇后,妈妈回家的速度为______m/min;
(4)______min时,两人相距750m.
21、(8分)已知等腰直角△ABD和等腰直角△DFC如图放置,BD=AD,DF=DC,∠ADB=∠FDC=90°
,其中,B、D、C在一条直线上,连接BF并延长交AC于E.
(1)求证:
BF=AC;
(2)BF与AC有什么位置关系?
说明理由.
(3)若AB=BC,BF与AE有什么数量关系?
22、(12分)已知:
如图,等腰三角形ABC中,AB=AC,AD∥BC,CD∥AB,点E沿着BA从B向A运动,同时点F沿AC从A向C运动,E、F两点速度相同,当E到达A时,两点停止运动.
(1)图中有______对全等三角形.请你找一对说明理由,写出过程.
(2)在E、F运动过程中,图中阴影部分的面积是否发生变化?
(3)当CE平分∠ACB时,延长DF交CE于G,试说明∠CGF=∠B.
(4)在(3)的条件下,若∠ECA=∠ACD,请问此时E点和G点重合吗?
为什么?
四、计算题(本大题共2小题,共28分)
23、(18分)计算
(1)
(2)(2x-1)2(2x+1)2
(3)(1+a)(a-1)(a2+1)(a4-1)
(4)[(x+2y)2-(x+y)(3x-y)-5y2]÷
(-
x),其中x=-2,y=
.
24、(10分)对于一个两位数,十位数字是a,个位数字是b,总有a≥b,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”.例如,对两位数43来说,42+32=25,42-32=7,所以25和7分别是43的“平方和数”与“平方差数”.
(1)76的“平方和数”是______,“平方差数”是______.
(2)5可以是______的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”与它的“平方差数”相等,那么这个数满足什么特征?
(写出说明过程)
(5)若一个数的“平方差数”等于它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数______,______.
【第1题】
【答案】
A
【解析】
解:
A、是轴对称图形,故此选项正确;
B、不是轴对称图形,故此选项错误;
C、不是轴对称图形,故此选项错误;
D、不是轴对称图形,故此选项错误;
故选:
A.
根据轴对称图形的概念:
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
此题主要考查了轴对称图形,关键是掌握轴对称图形的概念.
【第2题】
C
x5+x5=2x5,故选项A错误;
(a-b)7÷
(a-b)3=(a-b)4,故选项B错误;
(-x5)5=-x25,故选项C正确;
(-x)5(-x)5=x10,故选项D错误.
C.
分别根据合并同类项的法则、同底数幂的除法法则、幂的乘方以及同底数幂的乘法法则化简即可得出正确选项.
本题主要考查了幂的运算,熟练掌握幂的运算法则是解答本题的关键.
【第3题】
如图,
∵a∥b,
∴∠1=∠4=120°
,
∵∠4=∠2+∠3,
而∠2=40°
∴120°
=40°
+∠3,
∴∠3=80°
由a∥b,根据平行线的性质得∠1=∠4=120°
,再根据三角形外角性质得∠4=∠2+∠3,所以∠3=∠4-∠2=80°
本题考查了平行线的性质:
两直线平行,同位角相等.也考查了三角形外角性质.
【第4题】
D
A、添加BC=EC,∠BCE=∠DCA可用SAS判定两个三角形全等,故A选项正确;
B、添加BC=EC,AB=DE可用SSS判定两个三角形全等,故B选项正确;
C、添加∠B=∠E,∠A=∠D可用AAS判定两个三角形全等,故C选项正确;
D、添加BC=EC,∠A=∠D后是SSA,无法证明三角形全等,故D选项错误.
D.
直接利用三角形全等的判定条件进行判定,即可求得答案;
注意而SSA是不能判定三角形全等的.
本题考查全等三角形的判定,解题的关键是熟练掌握基本知识属于中考常考题型.
【第5题】
B
由∠A=
∠C,易知∠A=30°
,∠B=60°
,∠C=90°
,故选项A不符合题意,
由∠A=∠B=
∠C,易知∠A=45°
,∠B=45°
,故选项B不符合题意
由∠A=2∠B=2∠C,易知∠A=90°
,∠C=45°
,故选项A不符合题意
B.
根据三角形内角和定理,求出A,B,C即可判断.
本题考查三角形内角和定理,解题的关键是熟练掌握基本知识,属于中考常考题型.
【第6题】
A、从一装有2个白球和1个红球的袋子中任取一球,取到红球的概率是
≈0.33;
B、掷一枚正六面体的骰子,出现1点的概率是
;
C、抛一枚硬币,出现正面的概率
D、任意写一个整数,它能被2整除的概率,即为偶数的概率为
由用频率去估计概率的统计图可知当试验次数到600次时频率稳定在33%左右,故符合条件的只有A.
分析四个选项中的概率,为33%左右的符合条件.
本题考查了概率的知识.用到的知识点为:
概率=所求情况数与总情况数之比.
【第7题】
由点P的运动可知,当点P在GF、ED边上时△ABP的面积不变,则对应图象为平行于t轴的线段,则B、C错误.点P在AD、EF、GB上运动时,△ABP的面积分别处于增、减变化过程.故D排除
分析动点P在每段路径上的运动的过程中的面积增大、减小或不变的趋势即可.
本题为动点问题的函数图象判断题,考查学生对于动点运动过程中函数图象的变化趋势的判断.解答关键是注意动点到达临界点前后的图象变化.
【第8题】
∵CA=CB,∠C=90°
∴∠B=45°
∵DE⊥AB,
∴∠DEB=90°
∴∠EDB=∠B=45°
∴ED=EB,
∵DA平分∠CAB,DC⊥AC,DE⊥AB,
∴CD=DE=EB=a,
∵DC=DE,AD=AD,∠C=∠AED=90°
∴Rt△ADC≌Rt△ADE(HL),
∴AE=AC=BC=a+b,
∴AB=AE+BE=2a+b,
只要证明AC=AE=BC=a+b,CD=DE=BE=a即可解决问题.
本题考查角平分线的性质定理,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【第9题】
4.8×
10-6
0.0000048=4.8×
10-6,
故答案为:
10-6.
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×
10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为a×
10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
【第10题】
-
原式=-
+1-1
=-
直接利用零指数幂的性质以及负指数幂的性质分别化简得出答案.
此题主要考查了零指数幂的性质以及负指数幂的性质,正确化简各数是解题关键.
【第11题】
个位上的数字共0~9十种情况,
故P(个位数字是5)=
列举出个位数上数字的所有情况即可求得个位数字是5的概率.
本题考查了概率的公式,属于概率的基本情况,比较简单.
【第12题】
108°
如图,延长AB交DR于T.
∵BC∥DE,
∴∠ABC=∠ATR=38°
∵AT∥EC,
∴∠CER=∠ATR=38°
∴∠DEB=∠CEB=
(180°
-38°
)=71°
∴∠DEF=180°
-∠DEB=108°
故答案为108°
如图,延长AB交DR于T.想办法求出∠DEB即可解决问题.
本题考查了平行线的性质,翻折变换的性质,邻补角定义的应用,熟记折叠的性质是解题的关键.
【第13题】
40°
如图,∵∠C=90°
,∠ABC=35°
∴∠TAF=∠CAB=90°
-35°
=55°
∵∠T=45°
∴∠AFT=180°
-45°
-55°
=80°
∴∠DFE=∠AFT=80°
∵∠D=60°
-80°
-60°
故答案为40°
根据三角形内角和定理求出∠DFE即可.
本题考查三角形内角和定理,三角板的内角的度数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【第14题】
16
∵DE,FG分别是△ABC的AB,AC边的垂直平分线,
∴AE=BE,CG=AG,
∵BC=12,GE=2,
∴AE+AG=BE+CG=12+2=14,
∴△AGE的周长是AG+AE+EG=14+2=16,
根据线段垂直平分线性质得出AE=BE,CG=AG,求出AE+AG=BE+CG=12即可解决问题.
本题考查了线段垂直平分线性质,注意:
线段垂直平分线上的点到线段两个端点的距离相等.
【第15题】
-1008
a1=0,
a2=-|a1+1|=-|0+1|=-1,
a3=-|a2+2|=-|-1+2|=-1,
a4=-|a3+3|=-|-1+3|=-2,
a5=-|a4+4|=-|-2+4|=-2,
…,
所以,n是奇数时,an=-
,n是偶数时,an=-
a2017=-
=-1008.
-1008.
根据条件求出前几个数的值,再分n是奇数时,结果等于-
,n是偶数时,结果等于-
,然后把n的值代入进行计算即可得解.
本题是对数字变化规律的考查,根据所求出的数,观察出n为奇数与偶数时的结果的变化规律是解题的关键.
【第16题】
如图作等F关于AD的对称点F′,连接EF′.作BH⊥AC于H.
∵AB=AC,AD⊥BC,
∴BD=CD=3,
∴点F′在AC上,
∵BE+EF=BE+EF′,
根据垂线段最短可知,当B,E,F′共线,且与H重合时,BE+EF的值最小,最小值就是线段BH的长.
在Rt△ACD中,AC=
=5,
∵
•BC•AD=
•AC•BH,
∴BH=
∴BE+EF的最小值为
故答案为
如图作等F关于AD的对称点F′,连接EF′.作BH⊥AC于H.根据垂线段最短可知,当B,E,F′共线,且与H重合时,BE+EF的值最小,最小值就是线段BH的长.
本题考查轴对称-最短问题,等腰三角形的性质,解直角三角形等知识,解题的关键是学会利用轴对称解决最值问题,属于中考常考题型.
【第17题】
△ABC为所作.
先∠MBN=∠1,在BM上截取BA=2a,然后以A点为圆心,BA为半径画弧交BN于C,则△ABC满足条件.
本题考查了作图-复杂作图:
复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
【第18题】
∠ABC
∠ADC
∠ABC
同角的补角相等
∠EBF
∠ADF
∠AEB
∵AD∥BC,
∴∠A+∠ABC=180°
(两直线平行,同旁内角互补),
∵AB∥CD,
∴∠A+∠ADC=180°
∴∠ABC=∠ADC(同角的补角相等),
又∵BE平分∠ABC,
∴∠EBF=
∠ABC(角平分线定义),
∴∠ADF=
∠ADC(角平分线定义),
∴∠EBF=∠ADF,
∴∠AEB=∠EBF(两直线平行,内错角相等),
∴∠AEB=∠ADF(等量代换),
∴BE∥DP(同位角相等,两直线平行),
∠ABC,∠ADC,∠ABC,∠ADC,同角的补角相等,∠EBF,∠ADF,∠EBF,∠ADF,∠EBF,∠AEB,∠ADF.
根据平行线的性质得出∠A+∠ABC=180°
,∠A+∠ADC=180°
,求出∠ABC=∠ADC,根据角平分线定义求出∠EBF=∠ADF,求出∠AEB=∠ADF即可.
本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键.
【第19题】
∵正方形的面积为9,阴影部分的面积为1+
×
1×
4=3,
∴
=
∴小明获胜的概率为
,小丽获胜的概率为1-
>
∴不公平.
戏是否公平,求出游戏双方获胜的概率,比较是否相等即可.
本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:
【第20题】
(1)由图象可得,
小东打电话时,他离家1400m,
1400;
(2)由图可得,
小东行驶6min对应的y的值为:
1400-6×
100=800,
小东行驶到22min时对应的y值为:
(1400-6×
100)+(22-6)×
100=2400,
小东行驶到27min时对应的y值为:
100)+(27-6)×
100=2900,
故答案为,800,2400,2900;
(3)小东和妈妈相遇后,妈妈回家的速度为:
=50(m/min),
50;
(4)设在tmin时,两人相距750m,
相遇前相距750m,t=
相遇后相距750m,t=6+
=11,
或11.
(1)根据函数图象可以直接得到小东打电话时,他离家的距离;
(2)根据函数图象中的数据,可以算出图中空格中应填入的数据;
(3)根据函数图象中的数据可以计算出小东和妈妈相遇后,妈妈回家的速度;
(4)根据题意和图象中的数据,可以计算出两人相距750m对应的时间
本题考查函数图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【第21题】
(1)证明:
在△BDF和△ADC中,
∴△BDF≌△ADC(SAS)
∴BF=AC;
(2)解:
BF⊥AC,
理由如下:
∵△BDF≌△ADC,
∴∠DBF=∠DAC,
∵∠DBF+∠DFB=90°
,∠DFB=∠EFA,
∴∠EFA+∠DAC=90°
∴∠BEA=90°
∴BF⊥AC;
(3)解:
若AB=BC,则BF=2AE,
∵AB=BC,BF⊥AC,
∴AE=
AC,
∵BF=AC,
∴BF=2AE.
(1)利用SAS定理证明△BDF≌△ADC,根据全等三角形的性质证明结论;
(2)根据全等三角形的性质得到∠DBF=∠DAC,证明∠BEA=90°
,根据垂直的定义证明;
(3)根据等腰三角形的三线合一得到AE=
AC,根据
(1)中结论证明即可.
本题考查的是全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.
【第22题】
(1)△ABC≌△CDA,△BCE≌△DAF,△AEC≌△CFD,
证明△ABC≌△CDA,
∵AD∥BC,CD∥AB,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠ADC,
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
3;
(2)在E、F运动过程中,图中阴影部分的面积不发生变化,
由题意得,BE=AF,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DAC=∠ACB,
∴∠DAC=∠B,
在△BCE和△DAF中,
∴△BCE≌△DAF(SAS),
∴图中阴影部分的面积=△ABC的面积,
∴在E、F运动过程中,图中阴影部分的面积不发生变化;
(3)∵BE=AF,
∴AE=CF,
在△AEC和△CFD中,
∴△AEC≌△CFD(SAS)
∴∠AEC=∠DFC,
∴∠BEC=∠GFC,
∵∠BCE=∠ACE,
∴∠CGF=∠B.
(4)∵AB∥CD,
∴∠BAC=∠ACD,
∵∠ECA=∠ACD,
∴∠ECA=∠BAC,
∴EA=EC,
∵CF=AE,
∴CF=CE,
在△BCE和△GCF中,
∴△BCE≌△GCF(AAS)
∴BC=GC,
∵∠EAC=∠ECA,∠BCE=∠ACE,
∴∠BEC=∠ACB,
∵∠ACB=∠B,
∴∠BEC=∠B,