中考题选力学教师版Word格式.docx
《中考题选力学教师版Word格式.docx》由会员分享,可在线阅读,更多相关《中考题选力学教师版Word格式.docx(20页珍藏版)》请在冰豆网上搜索。
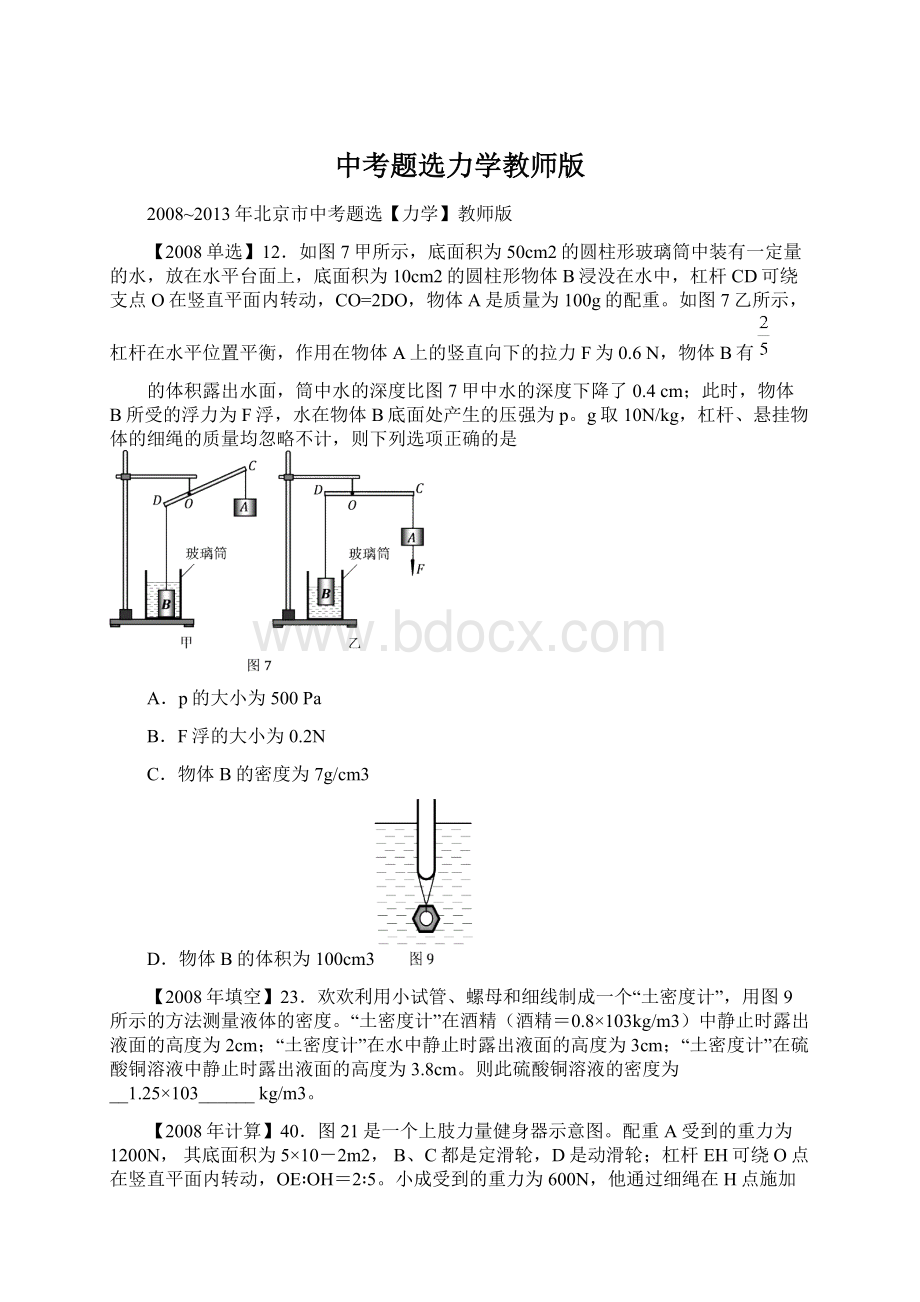
10-2m2=300N
N2=p2S=4×
10-2m2=200N
解得:
FA1=900N;
FA2=1000N……(1分)
(2)以人为研究对象,受力分析如图8甲、乙所示。
人始终处于静止状态,所以有:
G人=F1+T1
G人=F2+T2
因为T1与T1大小相等,F1与F1大小相等,
T2与T2大小相等,F2与F2大小相等。
所以有:
F1=G人-T1
F2=G人-T2…………………(1分)
已知F1∶F2=20∶19
得:
=
①
对杠杆进行受力分析如图9甲、乙所示:
根据杠杆平衡条件:
(FA1+G)×
OE=T1×
OH
(FA2+G)×
OE=T2×
OH…………………(1分)
已知OE∶OH=2∶5,FA1=900N,FA2=1000N
T2-T1=20N②
FA2+G=5T2③
已知G人=600N,由①②解得:
T2=220N………………(1分)
(3)将T2=220N代入③得:
G=100N………………(1
【2009年单选】12.甲溢水杯盛满密度为ρ1的液体,乙溢水杯盛满密度为ρ2的液体。
将密度为ρ的小球A轻轻放入甲溢水杯,小球A浸没在液体中,甲溢水杯溢出液体的质量是32g。
将小球B轻轻放入乙溢水杯,小球B漂浮,有
体积露出液面,乙溢水杯溢出液体的质量是40g。
已知小球A与小球B完全相同,ρ大于ρ1。
则下列选项中正确的是
A.小球A的质量为32g
B.小球B的质量为8g
C.ρ1与ρ2之比为2:
3
D.ρ1与ρ2之比为24:
25
图8
【2009年填空】23.图8是小明用滑轮组提升水中物体A的示意图。
当物体A完全在水面下被匀速提升的过程中,物体A所受浮力为80N,小明对绳子竖直向下的拉力为F1,水平地面对小明的支持力为N1。
当物体A有
的体积露出水面且静止时,小明对绳子竖直向下的拉力为F2,水平地面对小明的支持力为N2。
已知动滑轮所受重力为120N,小明所受重力为600N,N1:
N2=13:
12。
不计绳重、滑轮与轴的摩擦以及水的阻力,则物体A所受重力为640N。
【2009年计算】40.图23是小刚设计的一个通过简单机械自动拉开开关的装置示意图,该装置主要由滑轮组、配重C、D以及杠杆AB组成,配重C通过细绳与动滑轮相连,配重C、D分别通过支架固连在杠杆AB两端。
杠杆的B端放在水平台面上,杠杆可以绕支点O在竖直平面内逆时针转动,开关被拉开前,杠杆在水平位置平衡。
已知动滑轮P的质量mP为0.2kg,OA:
OB=3:
1,配重D的质量mD为1.5kg,作用在D上的竖直向下的压力F为75N,刚好拉开开关所需的拉力T为6N。
杠杆、支架和细绳的质量均忽略不计,滑轮与转轴的摩擦、杠杆与轴的摩擦均忽略不计,g取10N/kg。
配重C的质量mc等于多少千克,开关刚好能被拉开?
【2009】40.解:
若开关刚好能被拉开,则拉力T等于6N,配重C的质量等于mC,此时,杠杆在水平位置平衡,杠杆的B端受水平台面的支持力为零。
分别以杠杆AB及配重D、动滑轮、配重C为研究对象,受力分析,如图4甲、乙、丙所示。
………(1分)
以杠杆AB及配重D为研究对象时,受力分析如图4甲所示,杠杆A端受到向下的压力为F1,杠杆B端受到向下的压力为F和重力GD,根据杠杆平衡条件有:
F1×
OA=(GD+F)×
OB………①…………………………(1分)
GD=mDg=1.5kg×
10N/kg=15N
将GD=15N,OA∶OB=3∶1,F=75N代入①式解得:
F1=30N………(1分)
以动滑轮为研究对象时,受力分析如图4乙所示,动滑轮受到向上的拉力为2T,受到向下的拉力为T1,受到向下的重力GP。
因为动滑轮受力平衡,所以有:
T1=2T—GP②…………………………………………………(1分)
GP=mPg=0.2kg×
10N/kg=2N
T=T=6N
将T=6N,GP=2N代入②式解得:
T1=10N………………………………………………………………(1分)
以配重C为研究对象时,受力分析如图4丙所示,配重C受到向下的重力为GC,受到向上的支持力为F1,受到向上的拉力为T1。
因为配重C受力平衡,所以有:
GC=T1+F1③……………………………………(1分)
T1=T1=10N,F1=F1=30N
将T1=10N,F1=30N代入③式解得:
GC=40N
mC=
=
=4kg………………………………………(1分)
(其他解法正确的,均可相应得分)
【2010年】12.如图8所示,将甲、乙两个容器放在水平桌面上,甲、乙两容器的底面积分别为S甲和S乙。
甲容器中盛有密度为ρ1的液体,乙容器中盛有密度为ρ2的液体。
现将体积相等的A、B两个物体分别放入甲、乙两容器后,物体A悬浮,物体B漂浮且有一半体积露出液面,此时两容器中液面相平。
液体对甲容器底部的压强为p1、压力为F1,液体对乙容器底部的压强为p2、压力为F2。
已知物体A与物体B
的密度之比为2:
3,S乙等于4S甲。
则
下列判断正确的是
A.pl=p2,F1>
F2
B.p1<
p2,12F1=F2
C.3p1=p2,6Fl=F2
D.p1>
p2,F1=4F2
【2010年填空】23.如图10甲所示,底面积为80cm2的圆筒形容器内装有适量
的液体,放在水平桌面上;
底面积为60cm2的圆柱形物
体A悬挂在细绳的下端静止时,细绳对物体A的拉力为
F1。
将物体A浸没在圆筒形容器内的液体中,静止时,
容器内的液面升高了7.5cm,如图10乙所示,此时细绳
对物体A的拉力为F2,物体A上表面到液面的距离为
h1。
然后,将物体A竖直向上移动h2,物体A静止时,
细绳对物体A的拉力为F3。
已知F1与F2之差为7.2N,
F2与F3之比为5:
8,h1为3cm,h2为为5cm。
不计绳重,
g取l0N/kg。
则物体A的密度是2.8×
103kg/m3。
【2010年计算】38.(2010·
北京)图21甲是海洋中学科技小组设计的打捞水中物体的装置示意图。
DB是以O点为转轴的水平杠杆,OD的长度为1.6m。
水平甲板上的配重E通过细绳竖直拉着杠杆D端,配重E的质量mE为225kg。
安装在杠杆DB上的行走装置由支架、动滑轮X、提升电动机、定滑轮K构成,行走装置的质量m为25kg。
电动机Q可以通过定滑轮S和动滑轮X拉动行走装置沿BO水平滑动。
固定在提升电动机下的定滑轮K和动滑轮M组成滑轮组Y,当行走装置处于杠杆DB上C点的位置时,提升电动机拉动绳子H端,通过滑轮组Y竖直提升水中的物体A。
物体A完全在水中匀速上升的过程中,滑轮组Y的机械效率为η1,甲板对配重E的支持力为N1;
物体A全部露出水面匀速竖直上升的过程中,滑轮组Y的机械效率为η2,甲板对配重E的支持力为N2。
滑轮组Y提升物体A的过程中,行走装置受到的水平拉力始终为零,杠杆DB在水平位置保持平衡。
已知物体A的质量mA为50kg,体积V为20dm3,N1与N2之比为3:
2,η1与η2之比为9:
10物体A被打捞出水面后,停留在一定高度,电动机Q开始拉动行走装置。
在行走装置以0.05m/s的速度水平匀速移动的过程中,拉力T所做的功随时间变化的图像如图21乙所示,行走装置受到的水平拉力为F。
细绳和杠杆的质量、滑轮与轴的摩擦、水对物体的阻力均忽略不计,g取10N/kg。
(1)OC的长度;
(2)拉力F。
分析:
(1)因为DOC是一个杠杆,已知DO的长度,所以要求解OC的长度时,可以结合杠杆的平衡条件F1L1=F2L2进行求解,因此需要求出D点和C点的动力和阻力;
对配重E的受力分析可以求解动力FD1=F'
D1,
对以行走装置、动滑轮M和物体A为研究对象,受力分析可以求解阻力FC1=F'
C1,具体如下:
首先对物体A进行受力分析,物体A受到竖直向下的重力和竖直向上的水的浮力及绳子的拉力,在三个力的作用下处于平衡状态,即合外力为零,可以求出绳子拉力的大小;
然后结合滑轮组的机械效率公式η=
进行推理求解计算出动滑轮的重力;
结合杠杆的平衡条件F1L1=F2L2可以求解出OC的长度;
(2)由表格可知做功W和做功时间t,
结合功率公式
可以求出功率的大小;
再结合机械功率P=Fv求解拉力的大小.
解答:
解:
(1)物体A在水中匀速上升h1的过程中,
F1=mAg﹣F浮
F浮=ρ水Vg=200N
F1=300N
此时,滑轮组的机械效率
物体A离开水面后匀速上升h2的过程中,滑轮组机械效率
根据η1:
η2=9:
10,解得:
G动=100N.
物体A在水中匀速上升过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图a所示,配重E的受力分析图如图b所示,杠杆上C点、D点受力分析图如图c所示.
FC1=G﹣F浮
G=mg+G动+mAgN1=mEg﹣FD1
F'
D1•OD=F'
C1•OC
FC1=F'
C1,FD1=F'
D1
物体A离开水面后匀速上升的过程中,以行走装置、动滑轮M和物体A为研究对象,受力分析图如图d所示,配重E的受力分析图如图e所示,杠杆C点、D点受力分析图如图f所示.
FC2=GN2=mEg﹣FD2
D2•OD=F'
C2•OC
FC2=F'
C2,FD2=F'
D2
N1:
N2=3:
2
OC=1.8OD=2.88m;
答:
OC的长度为2.88m;
(2)行走装置以v=0.05m/s的速度水平匀速移动的过程中,由图象可得拉力T的功率
P=
=5W
P=T×
2v,解得:
T=50N
F=2T=100N;
拉力F为100N.
点评:
此类问题是一道复杂的综合题目,要会正确的对物体进行受力分析,结合平衡状态求解出各力的大小,进而利用杠杆的平衡条件和机械效率计算公式进行分析求解.
【2011年】12.甲、乙两个圆柱形容器盛有相同深度的液体,放置于水平桌面上,如图7所示。
甲、乙两容器的底面积分别为S1和S2,且2S1=3S2。
甲容器中液体的密度为ρ1,液体对容器底产生的压强为p1。
乙容器中液体的密度为ρ2,液体对容器底产生的压强为p2,且p2=2p1。
将A球浸在甲容器的液体中,B球浸在乙容器的液体中,两容器中均无液体溢出。
液体静止后,甲、乙两容器底受到液体的压力相等,A、B两球所受浮力分别为F1和F2。
则下列判断正确的是
A.F1>F2,ρ1<ρ2B.F1=F2,ρ1<ρ2
C.F1<F2,ρ1>ρ2D.F1<F2,ρ1<ρ2
答案:
12.A
解析:
偏难题。
属于液体压强与浮力的综合问题。
密度大小关系不难判断,根据液体压强公式和题目条件即可。
关于浮力的比较,可以利用结论:
液体中加入某种固体,无论该固体是漂浮、悬浮还是沉底,液体对容器底部压力的增加量都等于该物体受到的浮力。
加入固体前液体对容器底部的压力可比较大小,加入固体后液体对底部压力相等,不难得出答案。
【2011年】23.将高为10cm的圆柱体甲放在水平地面上,细绳的一端系于圆柱体甲上表面的中央,另一端竖直拉着杠杆的A端。
当把质量为800g的圆柱体乙悬挂在杠杆的B端并处于圆柱形容器M中时,杠杆在水平位置平衡,如图所示,此时圆柱体甲对水平地面的压强为3200Pa。
把质量为900g的水注入容器M中,水未溢出,水静止后,水对容器M底面的压强为2500Pa,圆柱体甲对水平地面的压强为5000Pa。
已知:
AO:
OB=2:
3,容器M的底面积为60cm
2,不计杠杆的质量,g取10N/kg,则圆柱体甲的密度为kg/m3。
5.6×
103
【2011年计算】39.某科技小组设计的提升重物的装置如图甲所示。
图中水平杆CD与竖直杆EH、DI组合成支架固定在水平地面上。
小亮站在地面上通过滑轮组提升重物,滑轮
组由动滑轮Q和安装在水平杆CD上的两个定滑轮组成。
小亮以拉力F1匀速竖直提升物体A的过程中,物体A的速度为υ1,滑轮组的机械效率为ηA。
小亮以拉力F2匀速竖直提升物体B的过程中,物体B的速度为υ2,滑轮组的机械效率为ηB。
拉力F1、F2做的功随时间变化的图像分别如图乙中①、②所示。
υ1=3υ2,物体A的体积为VA,物体B的体积为VB,且3VA=2VB,物体A的密度为ρA,物体B的密度为ρB,且8ρA=7ρB。
(不计绳的质量,不计滑轮与轴的摩擦)
机械效率ηB与ηA之差。
【2009】39.解:
设物体A受的重力为GA,物体B受的重力为GB,动滑轮受的重力为G动。
匀速提升物体A时,以物体A和动滑轮的整体为研究对象,受力分析如图4甲所示。
匀速提升物体B时,以物体B和动滑轮的整体为研究对象,受力分析如图4乙所示。
由图4甲、乙得:
2F1=GA+G动2F2=GB+G动
又因为F1=F1F2=F2
所以
(1)
由题中W-t图像可知:
P1=
=90WP2=
=45W
由
υ1=3υ2解得:
(2)
由
(1)、
(2)解得:
(3)
由G=ρgV3VA=2VB8ρA=7ρB解得:
(4)
由(3)、(4)解得:
G动=
GAG动=
GB
ηA=
=70%
ηB=
=80%
ηB-ηA=80%-70%=10%
【2012】12.水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器,容器内分别盛有等质量的液体。
其中甲、乙、丁容器中的液体密度相同。
若将小球A放在甲容器的液体中,小球A静止时漂浮,此时甲容器对桌面的压力为F1;
若将小球A用一段不计质量的细线与乙容器底部相连,并使其浸没在该容器的液体中,小球A静止时乙容器对桌面的压力为F2;
若将小球A放在丙容器的液体中,小球A静止时悬浮,此时丙容器对桌面的压力为F3;
若将小球A放在丁容器的液体中,用一根不计质量的细杆压住小球A,使其浸没,且不与容器底接触,小球A静止时丁容器对桌面的压力为F4。
A.F2<
F1=F3<
F4B.F1=F2=F3<
F4
C.F1=F3<
F2<
F4D.F1=F2=F3=F4
【2012】23.如图6所示,圆柱形容器甲和乙放在水平桌面上,它们的底面积分别为200cm2和100cm2。
容器甲中盛有0.2m高的水,容器乙中盛有0.3m高的酒精。
若从两容器中分别抽出质量均为m的水和酒精后,剩余水对容器甲底部的压强为p水,剩余酒精对容器乙底部的压强为p酒精。
当质量m的范围为时,才能满足p水>p酒精。
(ρ酒精=0.8×
103kg/m3)800g<m<2400g
【2012】39.图18是一种新型吊运设备的简化模型示意图,图中虚线框里是滑轮组(未画出),滑轮组绳子的自由端由电动机拉动。
工人师傅用该吊运设备先后搬运水平地面上的圆柱形物体A和物体B。
物体A的底面积为SA,密度为ρA,高度为hA;
物体B的底面积为SB,密度为ρB,高度为hB。
当物体A所受竖直向上的拉力T1为1500N时,物体A静止,地面对物体A的支持力为N1。
挂在滑轮组挂钩上的物体A匀速竖直上升4m的过程中,电动机对滑轮组绳子自由端的拉力为F1,拉力F1做的功为W。
当物体B所受竖直向上的拉力T2为1000N时,物体B静止,地面对物体B的支持力为N2。
挂在滑轮组挂钩上的物体B以速度v匀速竖直上升的过程中,电动机对滑轮组绳子自由端的拉力F2为625N,拉力F2做功的功率P为500W,滑轮组的机械效率为80%。
N1=2N2,5SA=4SB,8ρA=7ρB,2hA=5hB。
不计绳的质量,不计滑轮与轴的摩擦。
(1)物体B匀速上升的速度v;
(2)拉力F1做的功W。
【2012】39.解:
(1)当物体A受拉力为T1时,以物体A为研究对象,受力分析
如
图3甲所示;
当物体B受拉力为T2时,以物体B为研究
对象,受力分析如图3乙所示。
由图3甲、乙得:
GA=T1+N1
GB=T2+N2
N1=2N2,5SA=4SB,8ρA=7ρB,2hA=5hB
T1=1500N,T2=1000N
因为G=mg=ρVg=ρgSh
所以GA=ρAgSAhA,GB=ρBgSBhB
GA=3500N
GB=2000N
设滑轮组的绳子段数为n,提升物体B时,机械效率η=
F2=625N,η=80%
n=4
拉力F2做功的功率P=
=nvF2
P=500W
v=0.2m/s
(2)匀速提升物体A时,以物体A和动滑轮的整体为研究对象,受力分析如图4甲所示。
由图4乙得:
4F2=GB+G动
G动=4×
625N―2000N=500N
由图4甲得:
4F1=GA+G动
F1=
=1000N
拉力F1做的功W=nF1h
h=4m
W=4×
1000N×
4m=1.6×
104J
【2013年】14.图7是利用滑轮组匀速提升水中圆柱体M的示意图,滑轮组固定在钢架上,滑轮组中的两个滑轮质量相等,绕在滑轮组上的绳子能承受的最大拉力为900N,连接圆柱体M与动滑轮挂钩的绳子能承受的最大拉力为3000N。
圆柱体M高为3m,底面积为0.02m2,密度为4.5*103kg/m3。
在绳端拉力F作用下,圆柱体M从其下表面距水面15m处匀速上升到其上表面与水面相平的过程中用了3min,在这个过程中,拉力F的功率为160W,滑轮组的机械效率为,钢架对定滑轮的拉力为T。
在圆柱体M被缓慢拉出水的过程中,圆柱体M的下表面受到水的压强为p。
不计绳重、轮与轴的摩擦及水的阻力,g取10N/kg。
下列选项中正确的是
A.压强p的最小值为15000Pa
B.拉力T的大小为2700N
C.拉力F的大小为640N
D.滑轮组的机械效率为90%
【2013年】24.将圆柱体B竖立在圆柱形容器A的水平底面上,圆柱体B对容器A底面的压强为0p。
向容器A内缓慢注水,记录注入水的质量m和所对应的水对容器A底面的压强p,记录的数据如下表所示。
已知圆柱体B的体积为32800cm,则0P等于Pa。
(g取10N/kg)
【2013年】40.如图所示,杠杆AD放在钢制水平凹槽BC中,杠杆AD能以B点或C点为支点在水平面内转动。
BC=0.2m。
细绳的一端系在杠杆的A端,另一端绕过动滑轮固定在天花板上,物体E挂在动滑轮的挂钩上。
浸没在水中的物体H通过细绳挂在杠杆的D端,与杠杆固定连接的水平圆盘的上表面受到的压力为F。
已知60N≤F≤200N,动滑轮的质量m0=1kg,物体H的密度ρ=2×
10³
kg/m³
。
AD=0.8m,CD=0.2m。
杠杆、圆盘、细绳的质量及摩擦均忽略不计,g取10N/kg。
为使杠杆AD保持水平平衡。
(1)物体E的最小质量m
(2)物体H的最小体积V