版二轮复习数学理重点生通用版讲义第一部分 专题三 导数的几何意义及简单应用.docx

版二轮复习数学理重点生通用版讲义第一部分 专题三 导数的几何意义及简单应用.docx

《版二轮复习数学理重点生通用版讲义第一部分 专题三 导数的几何意义及简单应用.docx》由会员分享，可在线阅读，更多相关《版二轮复习数学理重点生通用版讲义第一部分 专题三 导数的几何意义及简单应用.docx（24页珍藏版）》请在冰豆网上搜索。

版二轮复习数学理重点生通用版讲义第一部分专题三导数的几何意义及简单应用

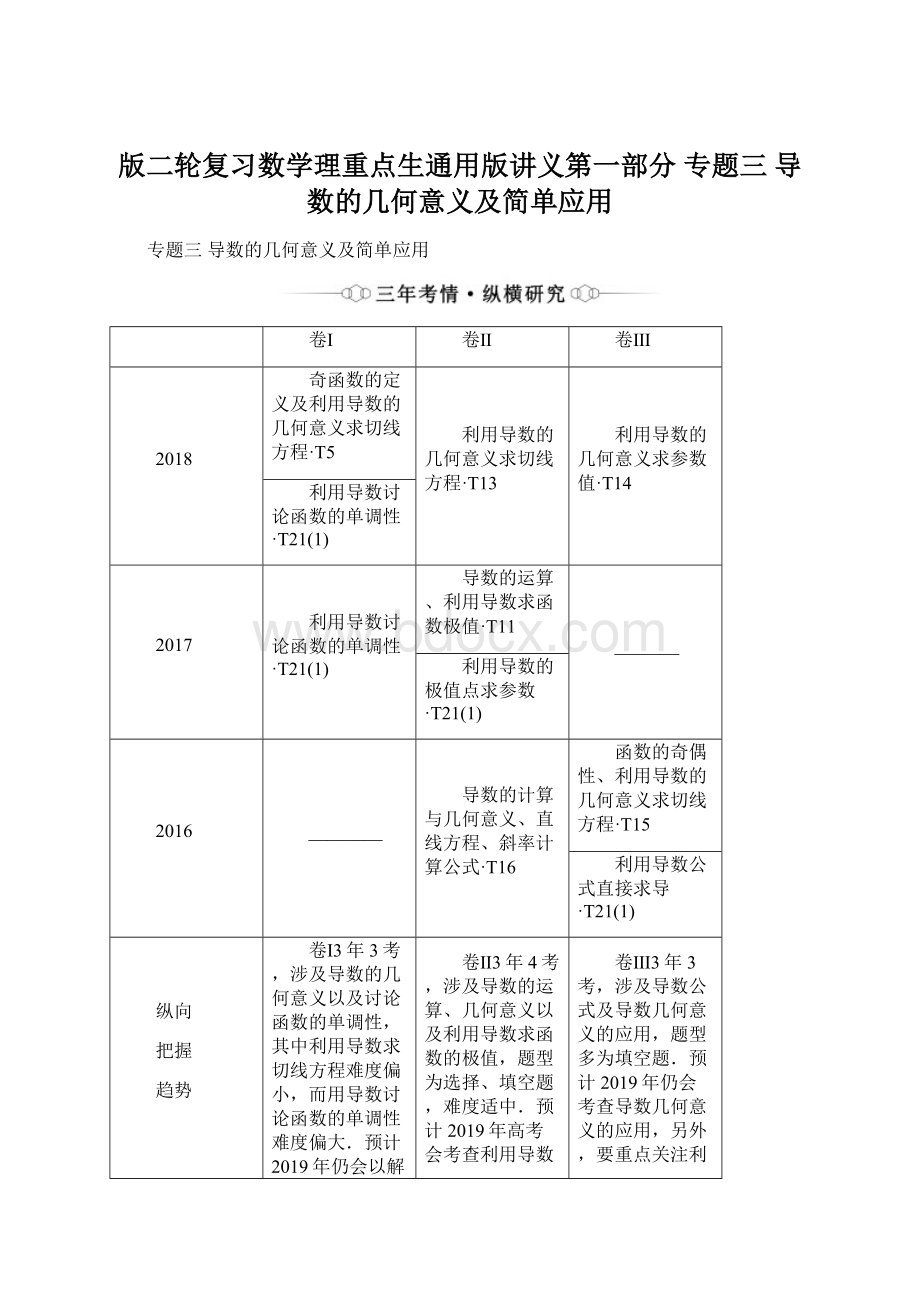
专题三导数的几何意义及简单应用

卷Ⅰ

卷Ⅱ

卷Ⅲ

2018

奇函数的定义及利用导数的几何意义求切线方程·T5

利用导数的几何意义求切线方程·T13

利用导数的几何意义求参数值·T14

利用导数讨论函数的单调性·T21

（1）

2017

利用导数讨论函数的单调性·T21

（1）

导数的运算、利用导数求函数极值·T11

_______

利用导数的极值点求参数·T21

（1）

2016

________

导数的计算与几何意义、直线方程、斜率计算公式·T16

函数的奇偶性、利用导数的几何意义求切线方程·T15

利用导数公式直接求导·T21

（1）

纵向

把握

趋势

卷Ⅰ3年3考，涉及导数的几何意义以及讨论函数的单调性，其中利用导数求切线方程难度偏小，而用导数讨论函数的单调性难度偏大．预计2019年仍会以解答题的形式考查函数单调性的讨论

卷Ⅱ3年4考，涉及导数的运算、几何意义以及利用导数求函数的极值，题型为选择、填空题，难度适中．预计2019年高考会考查利用导数讨论函数的单调性，难度偏大

卷Ⅲ3年3考，涉及导数公式及导数几何意义的应用，题型多为填空题．预计2019年仍会考查导数几何意义的应用，另外，要重点关注利用导数研究函数的单调性

横向

把握

重点

1.高考对导数的几何意义的考查，多在选择题、填空题中出现，难度较小．

2．高考重点考查导数的应用，即利用导数研究函数的单调性、极值、最值问题，多在选择、填空的后几题中出现，难度中等，有时也出现在解答题第一问．

3．近几年全国卷对定积分及其应用的考查极少，题目一般比较简单，但也不能忽略.

导数的几何意义

[题组全练]

1．（2018·全国卷Ⅰ）设函数f（x）＝x3＋（a－1）x2＋ax，若f（x）为奇函数，则曲线y＝f（x）在点（0,0）处的切线方程为（　　）

A．y＝－2x　　　　　　　　B．y＝－x

C．y＝2xD．y＝x

解析：

选D　∵f（x）＝x3＋（a－1）x2＋ax，

∴f′（x）＝3x2＋2（a－1）x＋a.

又∵f（x）为奇函数，∴f（－x）＝－f（x）恒成立，

即－x3＋（a－1）x2－ax＝－x3－（a－1）x2－ax恒成立，

∴a＝1，∴f′（x）＝3x2＋1，∴f′（0）＝1，

∴曲线y＝f（x）在点（0,0）处的切线方程为y＝x.

2．过点（0，－1）的直线l与曲线y＝lnx相切，则原点到l的距离为（　　）

A．1B.

C.D.

解析：

选C　设切点为（x0，lnx0）．

由y＝lnx，得y′＝，

所以直线l的斜率k＝y′|x＝x0＝，

所以切线方程为y－lnx0＝（x－x0），

即y＝x＋lnx0－1.

因为切线过点（0，－1），

则－1＝lnx0－1，

即x0＝1，

所以切线方程为y＝x－1，

即x－y－1＝0，

所以原点到l的距离d＝＝，故选C.

3．（2018·唐山模拟）曲线y＝与其在点（0，－1）处的切线及直线x＝1所围成的封闭图形的面积为（　　）

A．1－ln2B．2－2ln2

C．2ln2－1D．ln2

解析：

选C　因为y＝，所以y′＝′＝，则曲线y＝在（0，－1）处的切线的斜率k＝2，切线方程为y＝2x－1，则曲线y＝与其在点（0，－1）处的切线及直线x＝1所围成的封闭图形的面积S＝2x－1－dx＝2x－1－1＋dx＝[x2－2x＋2ln（x＋1）]＝2ln2－1.

4．（2018·全国卷Ⅲ）曲线y＝（ax＋1）ex在点（0,1）处的切线的斜率为－2，则a＝________.

解析：

∵y′＝（ax＋a＋1）ex，∴当x＝0时，y′＝a＋1，

∴a＋1＝－2，解得a＝－3.

答案：

－3

5．已知曲线y＝x＋lnx在点（1,1）处的切线与曲线y＝ax2＋（a＋2）x＋1相切，则a＝________.

解析：

由y＝x＋lnx，得y′＝1＋，则曲线y＝x＋lnx在点（1,1）处的切线斜率为2，故切线方程为y＝2x－1，与y＝ax2＋（a＋2）x＋1联立，得ax2＋ax＋2＝0，显然a≠0，所以由Δ＝a2－8a＝0⇒a＝8.

答案：

8

[系统方法]

1．求过切点切线问题的基本思路

设曲线在（x0，y0）处的切线为l，则根据

2．过非切点的切线的求法

设出切点坐标（x0，f（x0）），先求出在x＝x0处的切线方程，然后把所过点的坐标代入即求出x0，从而得出切线方程．

3．由曲线的切线求参数的方法

已知曲线在某点处的切线求参数的关键是用“方程思想”来破解，先求出函数的导数，从而求出在某点处的导数值；再根据导数的几何意义与已知条件，建立关于参数的方程，通过解方程求出参数的值．

利用导数研究函数的单调性

[多维例析]

角度一　讨论函数的单调性或求函数单调区间

　已知函数f（x）＝x2＋2cosx，g（x）＝ex·（cosx－sinx＋2x－2），其中e是自然对数的底数．

（1）求函数g（x）的单调区间；

（2）讨论函数h（x）＝g（x）－af（x）（a∈R）的单调性．

[解]　

（1）g′（x）＝（ex）′·（cosx－sinx＋2x－2）＋ex（cosx－sinx＋2x－2）′＝ex（cosx－sinx＋2x－2－sinx－cosx＋2）＝2ex（x－sinx）．

记p（x）＝x－sinx，

则p′（x）＝1－cosx.

因为cosx∈[－1,1]，所以p′（x）＝1－cosx≥0，所以函数p（x）在R上单调递增．

而p（0）＝0－sin0＝0，所以当x<0时，p（x）<0，g′（x）<0，函数g（x）单调递减；

当x>0时，p（x）>0，g′（x）>0，函数g（x）单调递增．

综上，函数g（x）的单调递减区间为（－∞，0），单调递增区间为（0，＋∞）．

（2）因为h（x）＝g（x）－af（x）＝ex（cosx－sinx＋2x－2）－a（x2＋2cosx），

所以h′（x）＝2ex（x－sinx）－a（2x－2sinx）

＝2（x－sinx）（ex－a）．

由

（1）知，当x>0时，

p（x）＝x－sinx>0；当x<0时，p（x）＝x－sinx<0.

当a≤0时，ex－a>0，

所以x>0时，h′（x）>0，函数h（x）单调递增；

x<0时，h′（x）<0，函数h（x）单调递减．

当a>0时，令h′（x）＝2（x－sinx）（ex－a）＝0，解得x1＝lna，x2＝0.

①若0

所以x∈（－∞，lna）时，ex－a<0，h′（x）>0，函数h（x）单调递增；

x∈（lna,0）时，ex－a>0，h′（x）<0，函数h（x）单调递减；

x∈（0，＋∞）时，ex－a>0，h′（x）>0，函数h（x）单调递增．

②若a＝1，则lna＝0，所以x∈R时，h′（x）≥0，函数h（x）在R上单调递增．

③若a>1，则lna>0，

所以x∈（－∞，0）时，ex－a<0，h′（x）>0，函数h（x）单调递增；

x∈（0，lna）时，ex－a<0，h′（x）<0，函数h（x）单调递减；

x∈（lna，＋∞）时，ex－a>0，h′（x）>0，函数h（x）单调递增．

综上所述，

当a≤0时，函数h（x）在（0，＋∞）上单调递增，在（－∞，0）上单调递减；

当0

当a＝1时，函数h（x）在R上单调递增；

当a>1时，函数h（x）在（－∞，0），（lna，＋∞）上单调递增，在（0，lna）上单调递减．

[类题通法]　讨论含参函数的单调性，其本质就是讨论导函数符号的变化情况，所以讨论的关键是抓住导函数解析式中的符号变化部分．讨论时要考虑参数所在的位置及参数取值对导函数符号的影响，一般来说需要进行四个层次的分类：

（1）最高次幂的系数是否为0；

（2）导函数是否有变号零点；

（3）导函数的变号零点是否在函数定义域或指定区间内；

（4）导函数的变号零点之间的大小关系．

角度二　已知函数的单调性求参数范围

　已知函数f（x）＝＋ax＋b（a，b∈R）．

（1）若函数f（x）在R上是增函数，求实数a的取值范围；

（2）若函数f（x）在（－1,3）上单调，求实数a的取值范围．

[解]　

（1）f′（x）＝＋a＝，

设g（x）＝1－x＋aex，由题意知g（x）≥0在R上恒成立，即1－x＋aex≥0在R上恒成立．

由ex>0，分离参数可得a≥在R上恒成立．

设h（x）＝，则h′（x）＝，

由h′（x）>0，得x<2；由h′（x）<0，得x>2，

所以h（x）在（－∞，2）上单调递增，在（2，＋∞）上单调递减，

所以h（x）max＝h

（2）＝，故a≥.

所以a的取值范围为.

（2）函数f（x）在（－1,3）上单调，则函数f（x）在（－1,3）上单调递增或单调递减．

①若函数f（x）在（－1,3）上单调递增，则f′（x）＝≥0在（－1,3）上恒成立，即1－x＋aex≥0在（－1,3）上恒成立，所以a≥在（－1,3）上恒成立．

设h（x）＝，则h′（x）＝，所以h（x）在（－1,2）上单调递增，在（2,3）上单调递减，

所以h（x）max＝h

（2）＝（x∈（－1,3）），故a≥.

所以a的取值范围为，＋∞.

②若函数f（x）在（－1,3）上单调递减，则f′（x）＝≤0在（－1,3）上恒成立，即1－x＋aex≤0在（－1,3）上恒成立，所以a≤在（－1,3）上恒成立．

设h（x）＝，则h′（x）＝，所以h（x）在（－1,2）上单调递增，在（2,3）上单调递减．

又h（－1）＝＝－2e，h（3）＝＝.

显然－2e<，所以h（x）>h（－1）＝－2e（x∈（－1,3）），

所以a的取值范围为（－∞，－2e]．

综上，a的取值范围为（－∞，－2e]∪.

[类题通法]

由含参函数单调性求解参数范围问题的2个关注点

（1）准确把握函数单调性与导函数符号之间的关系：

若可导函数f（x）在区间M上单调递增，则f′（x）≥0在区间M上恒成立；若可导函数f（x）在区间M上单调递减，则f′（x）≤0在区间M上恒成立．

（2）注意参数在导函数解析式中的位置，先尝试分离参数，将问题的求解转化为求解对应函数的最值问题；若不能分离参数或分离参数后对应函数的单调性无法利用导数解决，则可以直接转化为求解含参函数的最值问题．

[综合训练]

1．已知a∈R，函数f（x）＝（－x2＋ax）ex（x∈R，e为自然对数的底数）．

（1）当a＝2时，求函数f（x）的单调递增区间；

（2）若函数f（x）在（－1,1）上单调递增，求a的取值范围；

（3）函数f（x）是否为R上的单调减函数？

若是，求出a的取值范围？

若不是，请说明理由．

解：

（1）当a＝2时，f（x）＝（－x2＋2x）ex，

所以f′（x）＝（－2x＋2）ex＋（－x2＋2x）ex＝（－x2＋2）ex.

令f′（x）>0，即（－x2＋2）ex>0，

因为ex>0，所以－x2＋2>0，

解得－

所以函数f（x）的单调递增区间是（－，）．

（2）因为函数f（x）在（－1,1）上单调递增，

所以f′（x）≥0对x∈（－1,1）都成立．

因为f′（x）＝（－2x＋a）ex＋（－x2＋ax）ex

＝[－x2＋（a－2）x＋a]ex，

所以[－x2＋（a－2）x＋a]ex≥0对x∈（－1,1）都成立．

因为ex>0，所以－x2＋（a－