模型参考MRAC自适应控制资料下载.pdf

模型参考MRAC自适应控制资料下载.pdf

《模型参考MRAC自适应控制资料下载.pdf》由会员分享，可在线阅读，更多相关《模型参考MRAC自适应控制资料下载.pdf（44页珍藏版）》请在冰豆网上搜索。

校正参数的自适应机制自适应机制能保证当参数变化时系统稳定并使得跟踪误差收敛到零；

设计方法有李雅普诺夫定理，超稳定性理论，耗散理论等。

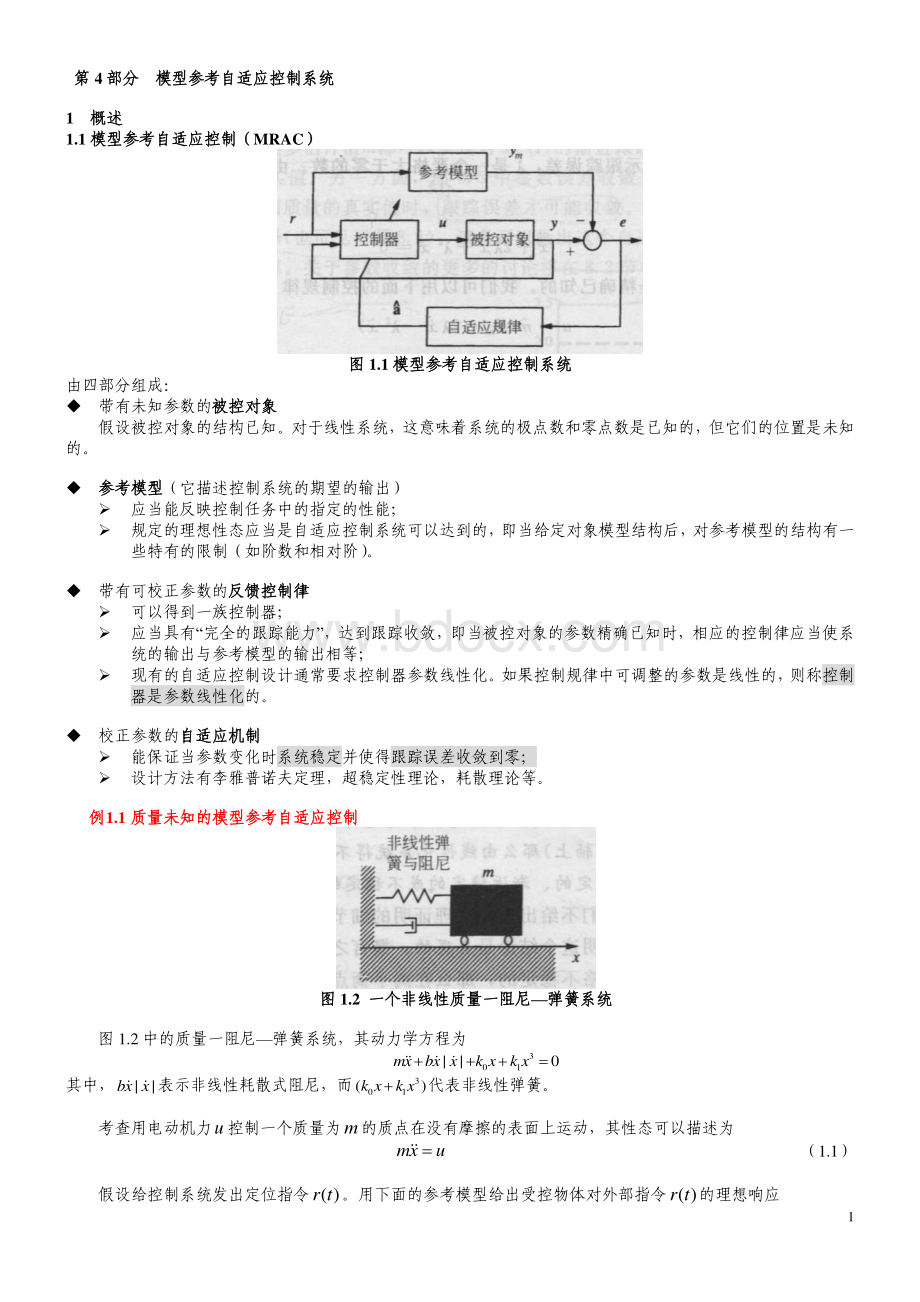
例例1.1质量未知的模型参考自适应控制质量未知的模型参考自适应控制图图1.2一个非线性质量一阻尼一个非线性质量一阻尼弹簧系统弹簧系统图1.2中的质量一阻尼弹簧系统，其动力学方程为301|0mxbxxkxkx其中，|bxx表示非线性耗散式阻尼，而301（）kxkx代表非线性弹簧。

考查用电动机力u控制一个质量为m的质点在没有摩擦的表面上运动，其性态可以描述为uxm（1.1）假设给控制系统发出定位指令）（tr。

用下面的参考模型给出受控物体对外部指令）（tr的理想响应2）（221trxxxmmm（1.2）其中，正常数1和2反映指定的性能，在理想情况下，物体应当像质量弹簧阻尼系统一样运动到指定的位臵）（tr。

若质量m精确已知，可以用下面的控制律实现完全跟踪）2（2xxxmum其中，）（）（txtxxm表示跟踪误差，是一个严格大于零的数。

由这个控制器可以得到按指数收敛的误差系统022xxx现在假设质量m不是精确已知的。

可以用下面的控制律）2（2xxxmum（1.3）其中，m表示可以校正的参数。

将这个控制律带入对象动态中，得到闭环误差动态vmmssm（1.4）其中，s是组合跟踪误差，定义为xxs（1.5）信号量v定义为xxxvm22参数估计误差m定义为mmm方程（1.4）表明组合跟踪误差s与参数误差通过一个稳定滤波器相关联。

m的参数更新规律vsm（1.6）其中正常数称为自适应增益。

注：

参数m的校正是基于系统的信号，自适应控制系统具有非线性本质，从而控制器（1.3）也是非线性的。

仿真分析：

设物体的真实质量是2m，选择零作为m的初值，这表明预先不知道真实质量。

自适应增益为5.0，分别选择其他设计参数为101，252，6。

图图1.3跟踪性能和未知质量参数的估计，跟踪性能和未知质量参数的估计，0）（tr图图1.4跟踪性能和未知质量参数的估计，跟踪性能和未知质量参数的估计，ttr4sin）（图1.3表示位臵指令为0）（tr，初始条件为0）0（）0（mxx，5.0）0（）0（mxx的仿真结果。

图1.4表示期望位臵是正弦函数ttr4sin）（的仿真结果。

两种情形下位臵跟踪误差均收敛到零，而只有后一种情形参数误差趋于零。

31.2模型参考自适应控制方法模型参考自适应控制方法（MRAC）和自校正控制方法和自校正控制方法（STC）的关系的关系STCMRAC更新参数是为了使得输入输出之间的拟合误差最小更新参数是为了使得被控对象和参考模型之间的跟踪误差最小具有更高的灵活性，可以将不同的估计器和控制器耦合起来（即估计和控制分离）控制律和自适应律的选择相对复杂一般很难保证自校正控制器的稳定性和收敛性。

通常要求系统的信号足够丰富，才能使得参数估计值收敛到真实值，才能保证系统的稳定性和收敛性。

不管信号充足与否，系统的稳定性和跟踪误差的收敛性通常是可以保证的从随机调节问题的研究中演化而来从确定自动伺服系统的最优控制中发展起来的通常用于离散时间系统一般用于连续时间系统42李雅普诺夫理论基础李雅普诺夫理论基础2.1非线性系统与平衡点非线性系统与平衡点1非线性系统非线性系统一个非线性动力系统可以用以下的非线性微分方程描述（,）txfx（2.1）其中，f是一个n1的非线性向量函数，而x是一个n1的状态向量。

状态数n称为系统的阶系统的阶。

状态向量的一个特定值对应于状态空间的一个点。

方程（2.1）的一个解（）tx对应于状态空间的一条曲线，通常称为状态轨线状态轨线或系统轨线系统轨线。

（2.1）可以表示一个无控制信号的动态系统（自由系统），也可以代表一个反馈控制系统的闭环动态。

如果系统的动态方程为（,）txfxu而设计的控制律为（,）tugx闭环系统的动态方程可以被改写成（2.1）的形式。

一类特殊的非线性系统是线性系统线性系统。

线性系统的动态方程为（）txAx其中，A（t）为一个nn矩阵。

2自治系统与非自治系统自治系统与非自治系统定义定义2.1非线性系统（2.1）称为自治的自治的，如果f不显含t，即如果系统方程可写作（）xfx（2.2）否则，该系统称为非自治的非自治的。

控制系统的非自治性可能来自模型或控制器。

设有一个时不变的动力学模型为（,）xfxu控制器是时变的，可能导致一个非自治的闭环系统，即如果u=g（x,t）。

例如，简单模型xxu，控制器是非线性非自治的（例如2sinuxt）。

线性时不变装臵的自适应控制器往往使闭环系统变为非线性和非自治的。

自治系统和非自治系统的基本区别在于：

自治系统的状态轨线不依赖于初始时刻，而非自治系统一般不是这样。

3平衡点平衡点定义定义2.2状态*x称为系统的一个平衡态平衡态（或平衡点平衡点），如果一旦*（）txx，则此后状态永远停留在*x。

数学上，这表明定常向量*x满足*（）0fx（2.3）平衡点可通过解（2.3）求得。

一个线性时不变系统xAx（2.4）当A非奇异时只有一个惟一的平衡点（原点0）。

当A奇异时，它有无数平衡点，即满足Ax=0的所有解。

这表明平衡点不是独立的。

例如：

0xx，x轴上所有的点都是它的平衡点。

例例2.1摆摆图图2.1摆摆5摆的性态可用以下的非线性自治方程来描述2sin0MRbMgR（2.5）这里R是摆长、M是质量、b是铰链的摩擦系数、g是重力加速度（常数），记12,xx。

则相应的状态方程为12xx（2.6a）2212sinbgxxxMRR（2.6b）于是，平衡点满足210,sin0xx因此，平衡点为（02,0）及（2,0），从物理意义上讲，它们分别对应摆的垂直向上及垂直向下的位臵。

平衡点的变换平衡点的变换设我们感兴趣的平衡点为*x，那么，引入新变量*yxx并将*yxx代入方程（2.2），即可得到关于变量y的方程*（）yfyx（2.7）当y=0时，对应于*xx，是（2.7）的一个平衡点。

因此，若要研究方程（2.2）在平衡点*x附近的性态，只要研究方程（2.7）在原点邻域原点邻域的性态即可。

62.2稳定的概念稳定的概念图图2.2稳定的概念稳定的概念1稳定性与不稳定性稳定性与不稳定性定义定义2.3一个平衡点x=0称为稳定的稳定的（也称李雅普诺夫意义下的稳定）（也称李雅普诺夫意义下的稳定），如果任给R0，总存在r0，使当|（0）|xr时，|（）|txR，t0。

如果x=0不是稳定的，则称为不稳定平衡点不稳定平衡点。

定义2.3可写成0,0,|（0）|0,|（）|RrrttRxx或等价地记作0,0,（0）0,（）rRRrttxBxB例例2.2范德波尔振子的不稳定性范德波尔振子的不稳定性范德波尔振子方程为12xx22112

（1）xxxx图图2.3范德波尔振子的不稳定原点范德波尔振子的不稳定原点控制系统性能要求由渐近稳定这个概念来描述。

2渐近稳定性渐近稳定性定义定义2.4平衡点0称为渐近稳定的渐近稳定的，如果它是稳定的，而且存在r0使当|（0）|xr时，（）,tt0x。

图2.2显示当系统轨线从球Br内出发的轨线均收敛到原点。

球Br称为平衡点的一个吸引域吸引域，是指最大的一个区域，使从此区域出发的一切轨线均收敛于原点。

一个李雅普诺夫稳定而又不是渐近稳定的平衡点称为临界平衡临界平衡点点。

上述定义表征了系统的局部性态。

73.局部稳定性与全局稳定性局部稳定性与全局稳定性定义定义2.5如果对任何初值渐近稳定成立，则这样的平衡点称为大范围渐近稳定，也称全局渐近稳定。

称为大范围渐近稳定，也称全局渐近稳定。

线性时不变系统的稳定性分三种：

渐近稳定、临界稳定和不稳定。

82.3李雅普诺夫李雅普诺夫直接方法直接方法李雅普诺夫直接方法的基本原理是一个基本物理现象的数学表达。

可以由一个标量函数的变化来判断一个系统的稳定性。

图图2.4一个非线性质量一阻尼一个非线性质量一阻尼弹簧系统弹簧系统图2.4中的质量一阻尼弹簧系统，其动力学方程为301|0mxbxxkxkx（2.8）这里|bxx表示非线性耗散式阻尼，而301（）kxkx代表非线性弹簧。

系统的全部机械能是它的动能与势能之和23224010101111（）（）d2224xVxmxkxkxxmxkxkx（2.9）机械能和前面定义的稳定性概念之间的联系机械能和前面定义的稳定性概念之间的联系能量为0对应于平衡点（,）00xx。

渐近稳定意味着机械能收敛到零。

不稳定对应于机械能的增长。

机械能作为一个标量以隐含形式影响着状态向量的幅值，而且系统的稳定性可以通过系统能量的变化来描述。

系统运动中能量的变化率为3301（）（）（|）|Vxmxxkxkxxxbxxbx（2.10）由于阻尼的存在，系统的能量不断减少，一直到质点停止运动，即。

0x。

2.3.1正定函数与李雅普诺夫函数正定函数与李雅普诺夫函数上述能量函数有两个性质：

第一个性质：

它除了x及x均为零的点外严格正；

第二个性质：

当x及x依动力学方程（2.8）变化时，该函数单调下降。

定义定义2.6一个标量连续函数V（x）称为局部正定的局部正定的，如果V（0）=0，且在一个球0RB内0（）0Vxx如果V（0）=0且上述性质在整个状态空间成立，则称V（x）为全局正定函数全局正定函数。

9图图2.5正定函数正定函数）,（21xxV的典型形式的典型形式例如函数22211（）（1cos）2VMRxMRgxx它是例2.1中摆的机械能，它是局部正定的。

又如非线性质量阻尼弹簧系统的机械能（2.9），它是全局正定的。

这个系统动能2（1/2）mx不是正定的。

类似地定义几个相关概念：

函数V（x）称为局部局部或全局负定的全局负定的，如果V（x）是局部或全局正定的；

V（x）是正半定的正半定的，如果V（0）=0且对一切x0，V（x）0；

V（x）是负半定的负半定的，如果V（x）是正半定的。

设x为自治系统（2.2）的状态，假定V（x）是可微的，它对时间的导数可以用链式法则得到d（）（）dVVVVtxx=fxxx通常将这个导数称为“V沿着系统轨线的导数沿着系统轨线的导数”。

定义定义2.7如果在一个球0RB内，函数V（x）是正定的正定的，且有连续偏导数,而且它沿系统（2.2）的任一状态轨线的导数为负半定的负半定的，即（）0Vx那么V（x）称为系统（系统（2.2）的李雅普诺夫函数）的李雅普诺夫函数。

图图2.6定义定义2.7在在n=