3.5三角形的内切圆PPT文档格式.ppt

3.5三角形的内切圆PPT文档格式.ppt

《3.5三角形的内切圆PPT文档格式.ppt》由会员分享，可在线阅读，更多相关《3.5三角形的内切圆PPT文档格式.ppt（14页珍藏版）》请在冰豆网上搜索。

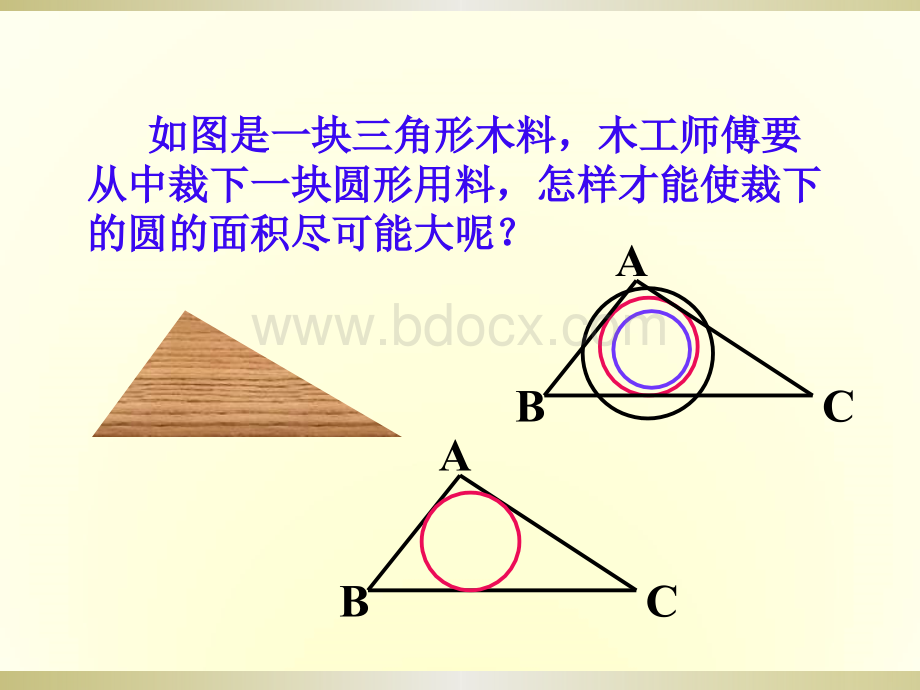
位置有什么特点？

圆心圆心0在在ABC的平分线上。

的平分线上。

2如图如图2，如果，如果O与与ABC的内角的内角ABC的两边的两边相切，且与内角相切，且与内角ACB的两的两边也相切，那么此边也相切，那么此O的圆心的圆心在什么位置？

在什么位置？

圆心圆心0在在BAC,ABC与与ACB的三个角的三个角的角平分线的交点上。

的角平分线的交点上。

OMABCNO图图2ABC作法作法：

ABC1、作、作B、C的平分线的平分线BM和和CN，交点为交点为I。

I2过点过点I作作IDBC，垂足为，垂足为D。

3以以I为圆心，为圆心，ID为半径为半径作作I.则则I就是所求的圆。

就是所求的圆。

MND画三角形的内切圆画三角形的内切圆定义：

定义：

和三角形各边都相切的圆叫做三角形的和三角形各边都相切的圆叫做三角形的内切圆内切圆，内切圆的圆心叫做三角形的，内切圆的圆心叫做三角形的内心内心，这个，这个三角形叫做圆的三角形叫做圆的外切三角形外切三角形。

1.1.三角形的内心到三角形各边的距离相等；

三角形的内心到三角形各边的距离相等；

性质性质：

CBADFEOr2.2.三角形的内心在三角形的角平分线上；

三角形的内心在三角形的角平分线上；

提示：

等边三角形的内切圆与外接圆是两个同心圆。

CCAABBRRrrOODD（A）1（B）12（C）12（D）12311、等边三角形的内切圆半径、外接圆的半径和高的比为（、等边三角形的内切圆半径、外接圆的半径和高的比为（）D（A）梯形（B）菱形（C）矩形（D）平行四边形2、下列图形中，一定有内切圆的四边形是（）B名称名称确定方法确定方法图形图形性质性质外心：

外心：

三角形三角形外接圆外接圆的圆心的圆心内心：

内心：

三角形三角形内切圆内切圆的圆心的圆心三角形三边三角形三边中垂线的交中垂线的交点点1.OA=OB=OC2.外心不一定外心不一定在三角形的内在三角形的内部部三角形三条三角形三条角平分线的角平分线的交点交点1.到三边的距离到三边的距离相等；

相等；

2.OA、OB、OC分别平分分别平分BAC、ABC、ACB3.内心在三角形内内心在三角形内部部oABCOABC探探讨讨11：

设设ABCABC的的内内切切圆圆的的半半径径为为rr，ABCABC的的各各边边长长之之和和为为CC，ABCABC的的面面积积SS,我我们会会有有什什么么结论?

COBADEF（CC为三角形周长，为三角形周长，rr为内切圆半径）为内切圆半径）rCS21=rABCOcDEr例：

直角三角形的两例：

直角三角形的两直角边分别是直角边分别是5cm5cm，12cm12cm则其内切圆的则其内切圆的半径为半径为_。

探讨探讨2：

如图，如图，直角三角形的两直角边分别是直角三角形的两直角边分别是aa，b,b,斜边为斜边为cc则其内切圆的半径为则其内切圆的半径为:

（以含、的代数式表示）（以含、的代数式表示）2cm2cmr=aba+b+crba变式练习1若直角三角形斜边长为10cm，其内切圆的半径为2cm，则它的周长为（）A24cmB22cmC14cmD12cmAACB古镇区古镇区镇镇商商业业区区镇工业区镇工业区.EDF如图，在进入镇区的道路交叉口的三角地处建造如图，在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑。

已知雕塑中心了一座镇标雕塑。

已知雕塑中心M到道路三边到道路三边AC、BC、AB的距离相等，的距离相等，ACBC，BC=30米，米，AC=40米。

米。

请你帮助计算一下，镇标雕塑中心请你帮助计算一下，镇标雕塑中心M离道路三边的距离道路三边的距离有多远？

离有多远？

M变式练习变式练习2CBAOIED如图如图,I,I是是ABCABC的内心的内心,连结连结AIAI并延长交并延长交BCBC边于点边于点D,D,交交ABCABC的外接圆于点的外接圆于点E.E.求证求证:

（1）EI=EB;

（2）IE=AEDE.2）5）3）4）1）例题拓展例题拓展小结：

小结：

（11）三角形的内心是三角形内切圆的圆心）三角形的内心是三角形内切圆的圆心（22）三角形的内心是三角形各角平分线的交点）三角形的内心是三角形各角平分线的交点（33）三角形内心到三边的距离相等）三角形内心到三边的距离相等（44）三角形面积）三角形面积（CC为三角形周长，为三角形周长，rr为内切圆半径）为内切圆半径）（5）（5）直角三角形直角三角形的内切圆的半径为的内切圆的半径为rr与与各边长各边长aa、bb、cc的关系是的关系是