必修2直线方程单元测试卷(三)Word文档下载推荐.doc
《必修2直线方程单元测试卷(三)Word文档下载推荐.doc》由会员分享,可在线阅读,更多相关《必修2直线方程单元测试卷(三)Word文档下载推荐.doc(8页珍藏版)》请在冰豆网上搜索。
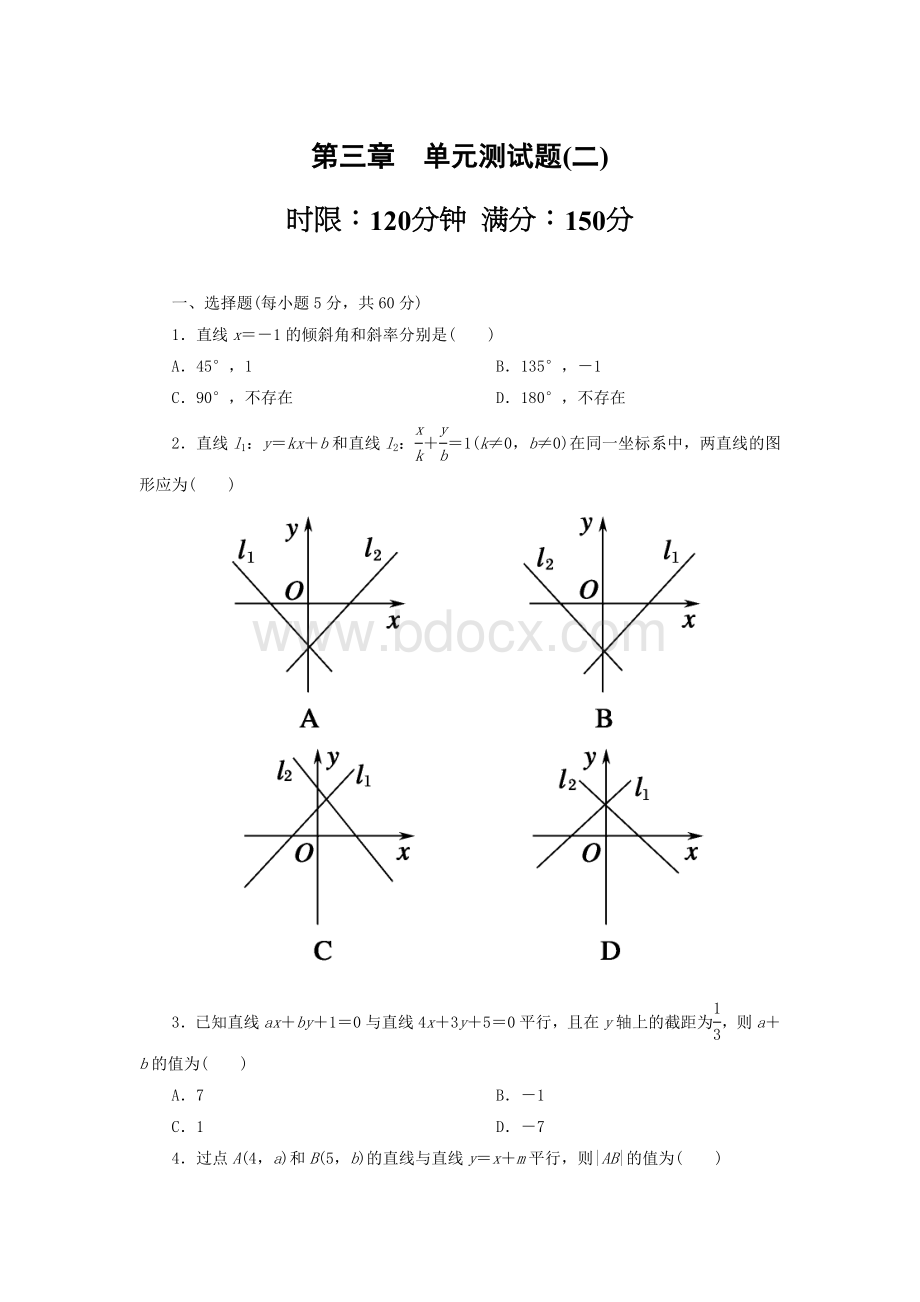
6.若A(-6,0)、B(0,8),点P在AB上,且AP∶AB=3∶5,则点P到直线15x+20y-16=0的距离为( )
A. B.
C. D.
7.已知点P(a,b)是第二象限内的点,那么它到x-y=0的距离是( )
A.(a-b) B.b-a
C.(b-a) D.
8.直线ax+y+m=0与直线x+by+2=0平行,则( )
A.ab=1,bm≠2
B.a=0,b=0,m≠2
C.a=1,b=-1,m≠2
D.a=1,b=1,m≠2
9.已知集合A={(x,y)|x+a2y+6=0},集合B={(x,y)|(a-2)x+3ay+2a=0},若A∩B=Ø
,则a的值是( )
A.3 B.0
C.-1 D.0或-1
10.已知点P(a,b)与点Q(b+1,a-1)关于直线l对称,则直线l的方程是( )
A.y=x-2 B.y=x+2
C.y=x+3 D.y=x-1
11.已知直线l1:
x+2y-6=0,l2:
x-y-3=0则l1、l2、x轴、y轴围成的四边形的面积为( )
A.8 B.6
C. D.3
12.如图1,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A.2 B.6
C.3 D.2
二、填空题(每小题5分,共20分)
13.直线y=-x+b与5x+3y-31=0的交点在第一象限,则b的取值范围是________.
14.直线l过两点A(0,2)和B(,3m2+12m+15)(m∈R),
则直线l倾斜角α的范围是________.
15.已知直线l1和l2的斜率是方程3x2-2x-1=0的两根,若直线l过点(2,3),斜率为两根之一,且不过第四象限,则直线l的方程为________________.
16.给出下列五个命题:
①过点(-1,2)的直线方程一定可以表示为y-2=k(x+1)的形式(k∈R);
②过点(-1,2)且在x轴、y轴截距相等的直线方程是x+y-1=0;
③过点M(-1,2)且与直线l:
Ax+By+C=0(AB≠0)垂直的直线方程是B(x+1)+A(y-2)=0;
④设点M(-1,2)不在直线l:
Ax+By+C=0(AB≠0)上,则过点M且与l平行的直线方程是A(x+1)+B(y-2)=0;
⑤点P(-1,2)到直线ax+y+a2+a=0的距离不小于2.
以上命题中,正确的序号是________.
三、解答题(共70分)
17.(本小题10分)已知直线l的斜率为6且被两坐标轴所截得的线段长为,求直线l的方程.
18.(本小题12分)将直线l绕它上面一点P按逆时针方向旋转角α(0°
<
α<
90°
)后,所得直线方程是6x+y-60=0.若再向同方向旋转90°
-α后,所得直线方程是x+y=0,求l的方程.
19.(本小题12分)求经过点A(-1,-2)且到原点距离为1的直线方程.
20.(本小题12分)已知直线l1:
2x+ay+4=0与直线l2平行,且l2过点(2,-2),并与坐标轴围成的三角形面积为,求a的值.
21.(本小题12分)甲、乙两人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°
,测得|AC|=5km,|BC|=km,|AO|=|BO|=2km,如图2所示,试问甲、乙两人应以什么方向走,才能使两人的行程之和最小?
图3
.
22.(本小题12分)四边形OABC的四个顶点坐标分别为O(0,0)、A(6,2)、B(4,6)、C(2,6),直线y=kx(<
k<
3)分四边形OABC为两部分,S表
示靠近x轴一侧的那一部分的面积.
(1)求S=f(k)的函数表达式;
(2)当k为何值时,直线y=kx将四边形OABC分为面积相等的两部分?
参考答案:
1.答案:
C
2.解析:
此题应从l1的位置判断k、b的正负,从而判定l2的位置.
答案:
D
3.解析:
由题意可知b≠0,方程可化为y=-x-.
则解得b=-3,a=-4,所以a+b=-7.
4.答案:
B
5.答案:
A
6.答案:
7.解析:
∵点P(a,b)是第二象限内的点,
∴a<
0,b>
0.∴a-b<
0.点P到直线x-y=0的距离为d==(b-a).
8.答案:
9.解析:
A∩B=Ø
,即直线l1:
x+a2y+6=0与l2:
(a-2)x+3ay+2a=0平行,
令1×
3a=a2(a-2),解得a=0或a=-1或a=3.
a=0时,l1:
x+6=0,l2:
x=0,l1∥l2.
a=-1时,l1:
x+y+6=0,l2:
-3x-3y-2=0.
l1∥l2.
a=3时,l1:
x+9y+6=0,l2:
x+9y+6=0,l1与l2重合,不合题意.
∴a=0或a=-1.
10.解析:
任取a、b进行赋值,如a=1,b=3,则点Q坐标为(4,0),求出其中点坐标为(,),它应该在直线l上.对各选项逐个检验可排除选项ABC.或得出点P、Q中点为(,),它应该是直线l上的点.故其满足方程y=x-1.
11.答案:
图1
12.解析:
直线AB的方程为x+y-4=0,点P关于直线AB的对称点P1坐标为(4,2),点P关于y轴的对称点P2(-2,0),则|P1P2|==2,即为光线所经过的路程.
13.解析:
解直线的方程组成的方程组,求出交点坐标,然后根据交点在第一象限列出不等式即可.
由⇒.
∵交点在第一象限,
∴,即⇒<
b<
.
14.解析:
由A,B的横坐标不等知α≠90°
,
则tanα=kAB=
=(m+2)2+,
∵m∈R,∴(m+2)2+≥,
即tanα≥,所以30°
≤α<
30°
15.答案:
x-y+1=0
16.答案:
④⑤
17.解:
设直线方程为y=6x+b,
令x=0,得y=b;
令y=0,得x=-.
∴直线与x轴、y轴的交点分别为(-,0)、(0,b),这两点间距离为
==|b|.
由题意,得|b|=,∴b=±
6.
∴所求直线方程为y=6x±
6,即6x-y±
6=0.
18.解:
由题意,得直线l与直线x+y=0垂直,且P点既在6x+y-60=0上,又在x+y=0上,所以P(12,-12),故其方程为y+12=x-12,即x-y-24=0.
19.解:
(1)当过点A的直线斜率不存在即垂直于x轴时,它到原点的距离为1,所以满足题设条件,其方程为x=-1.
(2)当过点A的直线不与x轴垂直时,
设所求的直线方程为y+2=k(x+1),
即kx-y+k-2=0.
因为原点到此直线的距离等于1,
所以=1,解之,得k=.
故所求的直线方程为y+2=(x+1),
即3x-4y-5=0.
故所求的直线方程为x=-1或3x-4y-5=0.
20.解:
由l2与l1:
2x+ay+4=0平行,可设l2的方程为2x+ay+k=0(k≠4).
令x=0,得y=-;
由·
|-|·
|-|=,得k2=4,
所以k=±
2且a>
0.
又2x+ay+k=0过点(2,-2),
所以有4-2a+k=0,从而a=1或a=3.
图2
21.解:
以O为原点,OB为x轴,建立直角坐标系(如图3所示),
设C(x,y),则有A(0,2),B(2,0),
由|AC|=5,有=5,①
|BC|=,有=.②
由①②解得或
由x、y的实际意义知x>
0,y>
0,∴C(5,2).
而A(0,2),∴AC∥x轴,即AC∥OB.
由B(2,0)、C(5,2),知kBC==.
故甲应以与OB平行的方向行走,乙应沿斜率为的直线向上方行走,才能使他们的行程和最小
22.解:
(1)因为kOB=,所以需分两种情况:
①<
时,直线y=kx与直线AB:
2x+y=14相交.
由得交点P1(,),
又点P1到直线OA:
x-3y=0的距离为
d=,
∴S=|OA|·
d=.
②当≤k<
3时,直线y=kx与直线BC:
y=6交于P2(,6).∴S△OP2C=|P2C|·
6=.
又S△OAB+S△OBC=S四边形OABC=20.
∴S=20-=26-.
故S=f(k)=
(2)若直线y=kx平分四边形OABC的面积,
由
(1)知,只需=10,解得k=.