初中数学相似三角形难题易错题附详解Word下载.docx

初中数学相似三角形难题易错题附详解Word下载.docx

《初中数学相似三角形难题易错题附详解Word下载.docx》由会员分享，可在线阅读，更多相关《初中数学相似三角形难题易错题附详解Word下载.docx（30页珍藏版）》请在冰豆网上搜索。

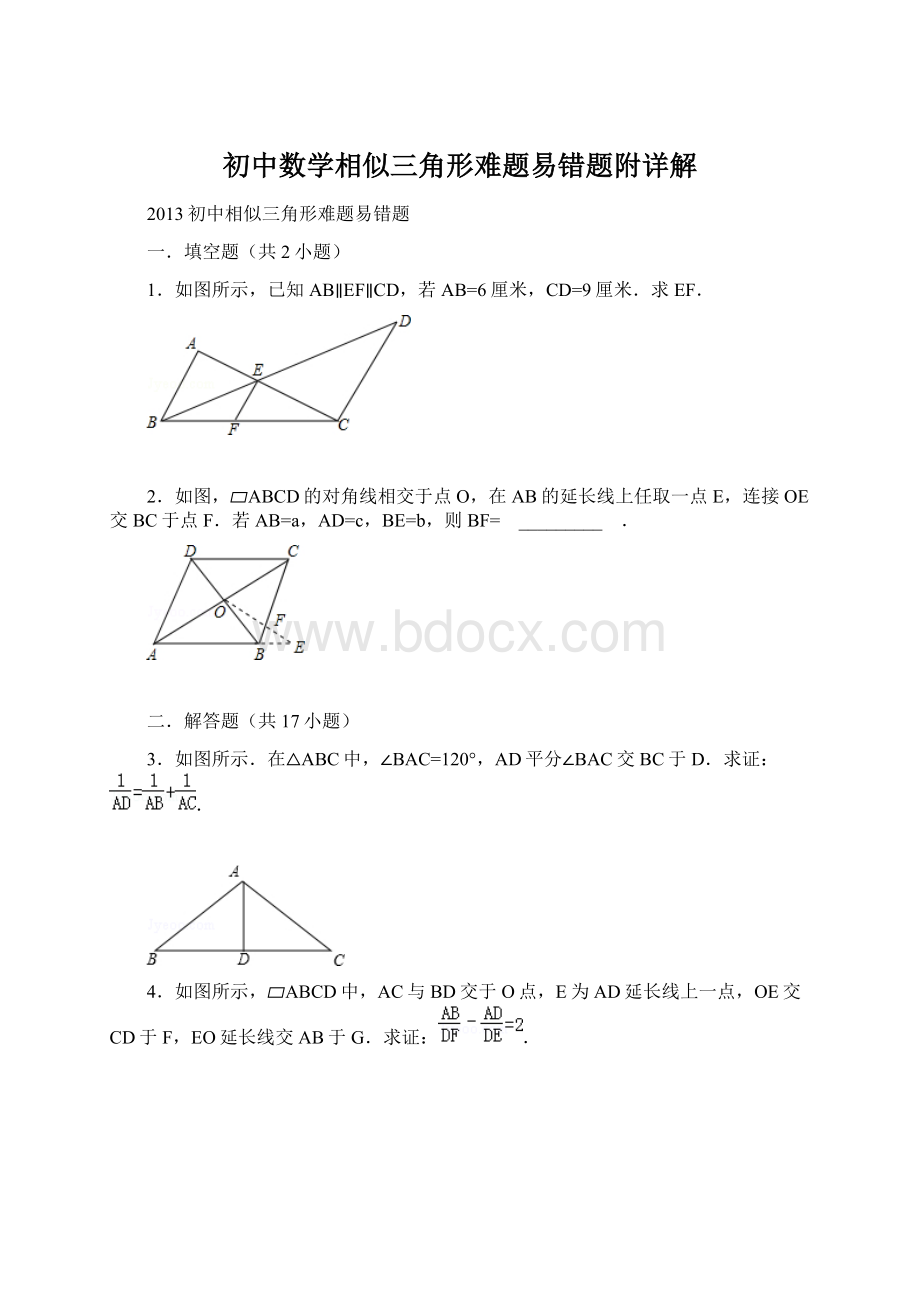
10．P为△ABC内一点，过P点作DE，FG，IH分别平行于AB，BC，CA（如图所示）．

求证：

．

11．如图所示．在梯形ABCD中，AB∥CD，AB＜CD．一条直线交BA延长线于E，交DC延长线于J，交AD于F，交BD于G，交AC于H，交BC于I．已知EF=FG=GH=HI=IJ，求DC：

AB．

12．已知P为△ABC内任意一点，连AP，BP，CP并延长分别交对边于D，E，F．

（1）

（2）三者中，至少有一个不大于2，也至少有一个不少于2．

13．如图所示．在△ABC中，AM是BC边上的中线，AE平分∠BAC，BD⊥AE的延长线于D，且交AM延长线于F．求证：

EF∥AB．

14．如图所示．P，Q分别是正方形ABCD的边AB，BC上的点，且BP=BQ，BH⊥PC于H．求证：

QH⊥DH．

15．已知M是Rt△ABC中斜边BC的中点，P、Q分别在AB、AC上，且PM⊥QM．求证：

PQ2=PB2+QC2．

16．如图所示．在△ABC中，∠ACB=90°

，CD⊥AB于D，AE平分∠CAB，CF平分∠BCD．求证：

EF∥BC．

17．如图所示．在△ABC内有一点P，满足∠APB=∠BPC=∠CPA．若2∠B=∠A+∠C，求证：

PB2=PA•PC．

（提示：

设法证明△PAB∽△PBC．）

18．已知：

如图，△ABC为等腰直角三角形，D是直角边BC的中点，E在AB上，且AE：

EB=2：

1．求证：

CE⊥AD．

19．如图所示，△ABC中，M、N是边BC的三等分点，BE是AC边上的中线，连接AM、AN，分别交BE于F、G，求BF：

FG：

GE的值．

20.在△ABC中，∠A∶∠B∶∠C=1∶2∶4．求证　　

提示：

要证明如几何题的常用方法：

①比例法：

将原等式变为，故构造成以a+b、b为边且与a、c所在三角形相似的三角形。

②通分法：

将原等式变为，利用相关定理将两个个比通分即：

参考答案与解析

　一．填空题（共2小题）

考点：

平行线分线段成比例．725636

专题：

计算题．

分析：

由于BC是△ABC与△DBC的公共边，且AB∥EF∥CD，利用平行线分线段成比例的定理，可求EF．

解答：

解：

在△ABC中，因为EF∥AB，

所以EF：

AB=CF：

CB①，

同样，在△DBC中有EF：

CD=BF：

CB②，

①+②得EF：

AB+EF：

CD=CF：

CB+BF：

CB=1③．

设EF=x厘米，又已知AB=6厘米，CD=9厘米，代入③得

x：

6+x：

9=1，

解得x=．

故EF=厘米．

点评：

考查了平行线分线段成比例定理，熟练运用等式的性质进行计算．

2．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB=a，AD=c，BE=b，则BF=　　．

相似三角形的判定与性质；

平行四边形的性质．725636

首先作辅助线：

取AB的中点M，连接OM，由平行四边形的性质与三角形中位线的性质，即可求得：

△EFB∽△EOM与OM的值，利用相似三角形的对应边成比例即可求得BF的值．

取AB的中点M，连接OM，

∵四边形ABCD是平行四边形，

∴AD∥BC，OB=OD，

∴OM∥AD∥BC，OM=AD=c，

∴△EFB∽△EOM，

∴，

∵AB=a，AD=c，BE=b，

∴ME=MB+BE=AB+BE=a+b，

∴BF=．

故答案为：

此题考查了平行四边形的性质、相似三角形的判定与性质等知识．解此题的关键是准确作出辅助线，合理应用数形结合思想解题．

等边三角形的判定．725636

证明题．

过D引DE∥AB，交AC于E，因为AD平分∠BAC（=120°

），所以∠BAD=∠EAD=60°

．若引DE∥AB，交AC于E，则△ADE为正三角形，从而AE=DE=AD，利用△CED∽△CAB，可实现求证的目标．

证明：

过D引DE∥AB，交AC于E．

∵AD是∠BAC的平分线，∠BAC=120°

，

∴∠BAD=∠CAD=60°

又∠BAD=∠EDA=60°

所以∴△ADE是正三角形，

∴EA=ED=AD．①

由于DE∥AB，所以△CED∽△CAB，

∴===1﹣．②

由①，②得=1﹣，

从而+=．

本题考查了相似三角形对应边比值相等的性质，考查了相似三角形的判定，考查了等边三角形的判定，考查了角平分线的性质，本题中求证△CED∽△CAB是解题的关键．

应利用平行四边形的性质，通过添加辅助线使各线段“集中”到一个三角形中来求证．

延长CB与EG，其延长线交于H，如虚线所示，构造平行四边形AIHB．

在△EIH中，由于DF∥IH，

∴=．

∵IH=AB，∴=，

从而，﹣=﹣===1+．①

在△OED与△OBH中，

∠DOE=∠BOH，∠OED=∠OHB，OD=OB，

∴△OED≌△OBH（AAS）．

从而DE=BH=AI，

∴=1．②

由①，②得﹣=2．

此题考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握，此题的关键是延长CB与EG，其延长线交于H，如虚线所示，构造平行四边形AIHB．这是此题的突破点，也是一个难点，因此属于一道难题．

5．一条直线截△ABC的边BC、CA、AB（或它们的延长线）于点D、E、F．

三角形的面积．725636

连接BE、AD，并把线段之比转化为两三角形面积之比，然后约分即可求证．

如图，连接BE、AD，

∵△BDE与△DCE等高，∴=，

∵△DCE与△ADE等高，∴=，

∵△ADF与△BDF等高，∴=，

∵△AEF与△BEF等高，∴=，

∴=，

∴••=••=1．

此题考查学生对三角形面积的理解和掌握，解答此题的关键是连接BE、AD，并把线段之比转化为两三角形面积之比．

平行四边形的判定与性质．725636

由FG∥BC，HI∥CA，ED∥AB，易证四边形AIPE、四边形BDPF、四边形CGPH均是平行四边形，利用平行线分线段成比例定理的推论可得△IHB∽△AFG∽△ABC，于是=，=，再结合=，先计算式子右边的和，易求++==2，从而有++=2，再把DE=FG=HI=d，AB=510，BC=450，CA=425代入此式，解即可．

∵FG∥BC，HI∥CA，ED∥AB，

∴四边形AIPE、四边形BDPF、四边形CGPH均是平行四边形，

∴△IHB∽△AFG∽△ABC，

∴=，=，

∴++=，

又∵DE=PE+PD=AI+FB，

AF=AI+FI，

BI=IF+FB，

∴DE+AF+BI=2×

（AI+IF+FB）=2AB，

∴++==2，

∵DE=FG=HI=d，AB=510，BC=450，CA=425，

∴++=++=2，

∴++=2，

解得d=306．

本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论、平行四边形的判定和性质．

由平行线的性质可得===，得出OE与BC，OF与AD的关系，进而即可求解EF的长．

∵AD∥BC，EF∥BC，

∴===，

又==，==，

∴OE=BC=，OF=AD=，

∴EF=OE+OF=15．

本题主要考查了平行线的性质问题，能够利用其性质求解一些简单的计算问题．

相似三角形的判定与性质．725636

由于AB=CD，所以将转化为，再由平行线的性质可得=，进而求解即可．

在平行四边形ABCD中，则AD∥BC，AB∥CD，

∴==

∴﹣=﹣==1．

本题主要考查了平行四边形的性质以及相似三角形的判定及性质问题，能够熟练掌握．

梯形．725636

由平行线分线段成比例可得对应线段的比，再由题中已知条件即可求解线段MN的长．

∵MN∥BC，∴在△ABD中，=，即OM==，

同理ON==，

∴MN=OM+ON=．

本题主要考查了平行线分线段成比例的性质问题，能够熟练掌握．

．

（1）由平行线可得△PIF∽△CAB，得出对应线