中考数学总复习动点问题练习含答案Word下载.doc

中考数学总复习动点问题练习含答案Word下载.doc

《中考数学总复习动点问题练习含答案Word下载.doc》由会员分享，可在线阅读，更多相关《中考数学总复习动点问题练习含答案Word下载.doc（4页珍藏版）》请在冰豆网上搜索。

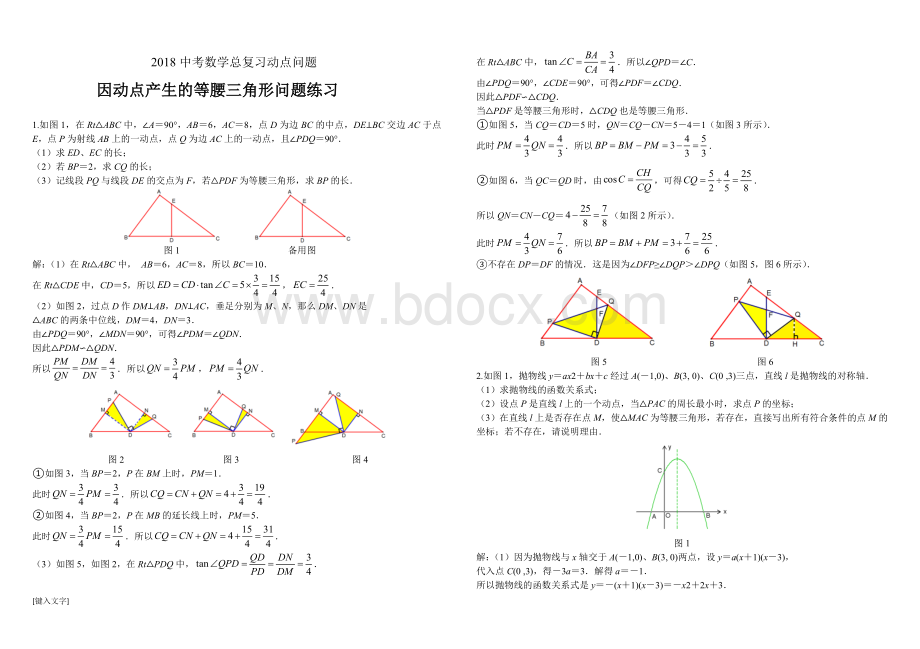
由∠PDQ＝90°

，∠MDN＝90°

，可得∠PDM＝∠QDN．

因此△PDM∽△QDN．

所以．所以，．

图2图3图4

①如图3，当BP＝2，P在BM上时，PM＝1．

此时．所以．

②如图4，当BP＝2，P在MB的延长线上时，PM＝5．

（3）如图5，如图2，在Rt△PDQ中，．

在Rt△ABC中，．所以∠QPD＝∠C．

，∠CDE＝90°

，可得∠PDF＝∠CDQ．

因此△PDF∽△CDQ．

当△PDF是等腰三角形时，△CDQ也是等腰三角形．

①如图5，当CQ＝CD＝5时，QN＝CQ－CN＝5－4＝1（如图3所示）．

②如图6，当QC＝QD时，由，可得．

所以QN＝CN－CQ＝（如图2所示）．

③不存在DP＝DF的情况．这是因为∠DFP≥∠DQP＞∠DPQ（如图5，图6所示）．

图5图6

2.如图1，抛物线y＝ax2＋bx＋c经过A（－1,0）、B（3,0）、C（0,3）三点，直线l是抛物线的对称轴．

（1）求抛物线的函数关系式；

（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；

（3）在直线l上是否存在点M，使△MAC为等腰三角形，若存在，直接写出所有符合条件的点M的坐标；

若不存在，请说明理由．

图1

（1）因为抛物线与x轴交于A（－1,0）、B（3,0）两点，设y＝a（x＋1）（x－3），

代入点C（0,3），得－3a＝3．解得a＝－1．

所以抛物线的函数关系式是y＝－（x＋1）（x－3）＝－x2＋2x＋3．

（2）如图2，抛物线的对称轴是直线x＝1．

当点P落在线段BC上时，PA＋PC最小，△PAC的周长最小．

设抛物线的对称轴与x轴的交点为H．

由，BO＝CO，得PH＝BH＝2．

所以点P的坐标为（1,2）．

图2

（3）点M的坐标为（1,1）、（1,）、（1,）或（1,0）．

3.如图1，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°

至OB的位置．

（1）求点B的坐标；

（2）求经过A、O、B的抛物线的解析式；

（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？

若存在，求点P的坐标；

（1）如图2，过点B作BC⊥y轴，垂足为C．

在Rt△OBC中，∠BOC＝30°

，OB＝4，所以BC＝2，．

所以点B的坐标为．

（2）因为抛物线与x轴交于O、A（4,0），设抛物线的解析式为y＝ax（x－4），

代入点B，．解得．

所以抛物线的解析式为．

（3）抛物线的对称轴是直线x＝2，设点P的坐标为（2,y）．

①当OP＝OB＝4时，OP2＝16．所以4+y2＝16．解得．

当P在时，B、O、P三点共线（如图2）．

②当BP＝BO＝4时，BP2＝16．所以．解得．

③当PB＝PO时，PB2＝PO2．所以．解得．

综合①、②、③，点P的坐标为，如图2所示．

图2图3

4.如图1，已知一次函数y＝－x＋7与正比例函数的图象交于点A，且与x轴交于点B．

（1）求点A和点B的坐标；

（2）过点A作AC⊥y轴于点C，过点B作直线l//y轴．动点P从点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；

同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．

①当t为何值时，以A、P、R为顶点的三角形的面积为8？

②是否存在以A、P、Q为顶点的三角形是等腰三角形？

若存在，求t的值；

图1

（1）解方程组得所以点A的坐标是（3，4）．

令，得．所以点B的坐标是（7，0）．

（2）①如图2，当P在OC上运动时，0≤t＜4．由，得．整理，得．解得t＝2或t＝6（舍去）．如图3，当P在CA上运动时，△APR的最大面积为6．

因此，当t＝2时，以A、P、R为顶点的三角形的面积为8．

图2图3图4

②我们先讨论P在OC上运动时的情形，0≤t＜4．

如图1，在△AOB中，∠B＝45°

，∠AOB＞45°

，OB＝7，，所以OB＞AB．因此∠OAB＞∠AOB＞∠B．

如图4，点P由O向C运动的过程中，OP＝BR＝RQ，所以PQ//x轴．

因此∠AQP＝45°

保持不变，∠PAQ越来越大，所以只存在∠APQ＝∠AQP的情况．

此时点A在PQ的垂直平分线上，OR＝2CA＝6．所以BR＝1，t＝1．

我们再来讨论P在CA上运动时的情形，4≤t＜7．

在△APQ中，为定值，，．

如图5，当AP＝AQ时，解方程，得．

如图6，当QP＝QA时，点Q在PA的垂直平分线上，AP＝2（OR－OP）．解方程，得．

如7，当PA＝PQ时，那么．因此．解方程，得．

综上所述，t＝1或或5或时，△APQ是等腰三角形．

图5图6图7

5.如图1，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．

（1）求y关于x的函数关系式；

（2）若m＝8，求x为何值时，y的值最大，最大值是多少？

（3）若，要使△DEF为等腰三角形，m的值应为多少？

（1）因为∠EDC与∠FEB都是∠DEC的余角，所以∠EDC＝∠FEB．又因为∠C＝∠B＝90°

，所以△DCE∽△EBF．因此，即．整理，得y关于x的函数关系为．

（2）如图2，当m＝8时，．因此当x＝4时，y取得最大值为2．

（3）若，那么．整理，得．解得x＝2或x＝6．要使△DEF为等腰三角形，只存在ED＝EF的情况．因为△DCE∽△EBF，所以CE＝BF，即x＝y．将x＝y＝2代入，得m＝6（如图3）；

将x＝y＝6代入，得m＝2（如图4）．

图2图3图4

6.如图1，在等腰梯形ABCD中，AD//BC，E是AB的中点，过点E作EF//BC交CD于点F，AB＝4，BC＝6，∠B＝60°

（1）求点E到BC的距离；

（2）点P为线段EF上的一个动点，过点P作PM⊥EF交BC于M，过M作MN//AB交折线ADC于N，连结PN，设EP＝x．

①当点N在线段AD上时（如图2），△PMN的形状是否发生改变？

若不变，求出△PMN的周长；

若改变，请说明理由；

②当点N在线段DC上时（如图3），是否存在点P，使△PMN为等腰三角形？

若存在，请求出所有满足条件的x的值；

图1图2图3

（1）如图4，过点E作EG⊥BC于G．

在Rt△BEG中，，∠B＝60°

，

所以，．

所以点E到BC的距离为．

（2）因为AD//EF//BC，E是AB的中点，所以F是DC的中点．

因此EF是梯形ABCD的中位线，EF＝4．

①如图4，当点N在线段AD上时，△PMN的形状不是否发生改变．

过点N作NH⊥EF于H，设PH与NM交于点Q．

在矩形EGMP中，EP＝GM＝x，PM＝EG＝．

在平行四边形BMQE中，BM＝EQ＝1＋x．

所以BG＝PQ＝1．

因为PM与NH平行且相等，所以PH与NM互相平分，PH＝2PQ＝2．

在Rt△PNH中，NH＝，PH＝2，所以PN＝．

在平行四边形ABMN中，MN＝AB＝4．

因此△PMN的周长为＋＋4．

图4图5

②当点N在线段DC上时，△CMN恒为等边三角形．

如图5，当PM＝PN时，△PMC与△PNC关于直线PC对称，点P在∠DCB的平分线上．

在Rt△PCM中，PM＝，∠PCM＝30°

，所以MC＝3．

此时M、P分别为BC、EF的中点，x＝2．

如图6，当MP＝MN时，MP＝MN＝MC＝，x＝GM＝GC－MC＝5－．

如图7，当NP＝NM时，∠NMP＝∠NPM＝30°

，所以∠PNM＝120°

又因为∠FNM＝120°

，所以P与F重合．

此时x＝4．

综上所述，当x＝2或4或5－时，△PMN为等腰三角形．

图6图7图8

[键入文字]