808.三角形的全等及其应用-奥数精讲与测试8年级.doc

808.三角形的全等及其应用-奥数精讲与测试8年级.doc

《808.三角形的全等及其应用-奥数精讲与测试8年级.doc》由会员分享，可在线阅读，更多相关《808.三角形的全等及其应用-奥数精讲与测试8年级.doc（5页珍藏版）》请在冰豆网上搜索。

beta.1三角形的全等及其应用姓名答疑信箱：

aoshu@

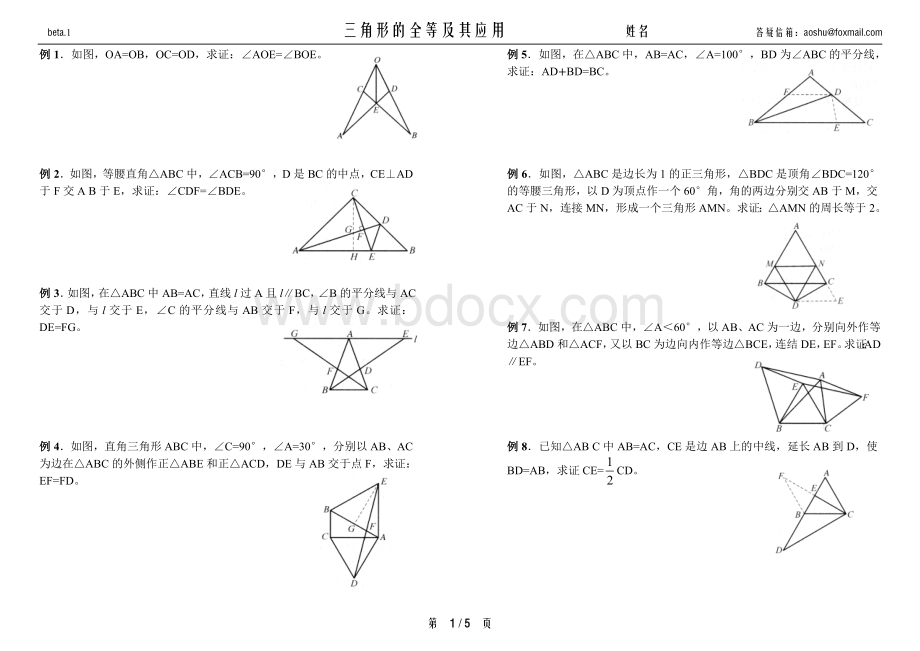
例1．如图，OA=OB，OC=OD，求证：

∠AOE=∠BOE。

例2．如图，等腰直角△ABC中，∠ACB=90°，D是BC的中点，CE⊥AD于F交AB于E，求证：

∠CDF=∠BDE。

例3．如图，在△ABC中AB=AC，直线l过A且l∥BC，∠B的平分线与AC交于D，与l交于E，∠C的平分线与AB交于F，与l交于G。

求证：

DE=FG。

例4．如图，直角三角形ABC中，∠C=90°，∠A=30°，分别以AB、AC为边在△ABC的外侧作正△ABE和正△ACD，DE与AB交于点F，求证：

EF=FD。

例5．如图，在△ABC中，AB=AC，∠A=100°，BD为∠ABC的平分线，求证：

AD+BD=BC。

例6．如图，△ABC是边长为1的正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB于M，交AC于N，连接MN，形成一个三角形AMN。

求证：

△AMN的周长等于2。

例7．如图，在△ABC中，∠A＜60°，以AB、AC为一边，分别向外作等边△ABD和△ACF，又以BC为边向内作等边△BCE，连结DE，EF。

求证：

AD∥EF。

例8．已知△ABC中AB=AC，CE是边AB上的中线，延长AB到D，使BD=AB，求证CE=CD。

A卷

一、填空题

01．如图9，等腰直角三角形ABC中，∠BAC=90°，∠CBA的平分线交AC于D，过C作BD的垂线，垂足为E，CE和BA的延长线相交于F。

若CE=5，则BD=________。

02．如图10，AE=AF，AB=AC，∠A=60°，∠B=24°，则∠BCE=________。

03．如图11，在等边△ABC中，AD=BE=CF，若三个全等的三角形为一组，则图中共有________组全等三角形。

04．如图12，D是等边△ABC内一点，DB=DA，BE=BC，∠DBE=∠DBC，则∠BED=_______。

05．如图13，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C=_______。

06．如图14，正方形ABCD边长为1，P、Q分别是边BC、CD上的点，连结PQ。

若△CPQ的周长是2，则∠PAQ=________。

07．如图15，C是线段BD上一点，分别以BC、CD为边长，在BD同侧作等边三角形BCA和等边三角形CDE，连结BE、AD，分别交AC于M，交CE于N。

若CM=x，则CN=________。

08．如图16，△ABD中，∠BAD=45°，AE⊥BD于E，DF⊥AB于F，交AE于G。

若BE=4，DE=4，则AG=________。

09．如图17，△ABC和△BDE都是等边三角形，且A、D、E在一条直线上。

若BE=2，CE=4，则AE=_______。

10.如图18，等边△ABC中，E、D分别是CA延长线，AB延长线上的点，且BD=AE，连结EB并延长交CD于F，则∠BFC=_______。

二、解答题

11．如图19，已知CD、BE相交于A，M是BC的中点，∠1=∠2，∠3=∠4，求证：

△BMD≌△CME。

12．如图20，已知过△ABC的顶点A，在∠BAC内部任意作一条射线，过B、C分别作此射线的垂线段BD、CE，M为BC中点。

求证：

MD=ME。

B卷

一、填空题

01．如图21，在△ABC中，∠A:

∠B:

∠C=3:

5:

10，又△≌△ABC，则∠:

∠=________。

02．如图22，设D是等边三角形ABC的AB边上一点，且DE⊥BC于E。

同理EF⊥AC于F，FD⊥AB于D。

若AB=3，则EC=________。

03．如图23，在△ABC中，∠B=70°，AD平分∠CAB，AC=AB+BD，则∠C=________。

04．如图24，已知△AEC是以正方形ABCD的对角线为边的等边三角形，EF⊥AB，交AB延长线于F，则∠BEF=________。

05．如图25，B在AC上，△ABE和△BCD都是等边三角形，M、N分别为AD、CE的中点，则△BMN是_______三角形。

06．如图26，△ABC是等腰直角三角形，∠C=90°，点M、N分别是边AC和BC的中点，点D在射线BM上，且BD=2BM；点E在射线NA上，且EN=2NA，则∠BDE=_______。

07．如图27，点D、E是正三角形ABC的边BC、AC上的点，且CD=AE，AD、BE相交于P点，BQ⊥AD。

已知PE=1，PQ=3，则AD=_______。

08．如图28，已知等边△ABC的边长为1，AB、AC上分别有两点M、N，∠MDN=60°，且∠BDC=120°，BD=CD，则△AMN的周长为_______。

09．如图29，△ABC、△EDC均为等边△，∠EBD=60°，则∠AEB=_______。

10．如图30，△ABC中，AB=4，AC=7，M是BC的中点，AD平分∠BAC，过M作FM∥AD，交AC于F，则FC=_______。

二、解答题

11．如图31，已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证：

AF=EF。

12．如图32，已知锐角△ABC中，BE、CF是高，在BE或CF的延长线上，分别截取BQ=CA，CP=BA，且⊥BC，⊥BC。

求证：

+=BC。

C卷

一、填空题

01．如图33，已知△ABC是等边△，E是AC延长线上的任一点，选择一点D，使△CDE为等边△。

如果M是线段AD的中点，N是线段BE的中点，则△CMN是________三角形。

02．如图34，△ABC中，∠BAC=60°，AD是∠BAC的平分线，且AC=AB+BD，则∠ABC=________。

03．如图35，四边形ABCD中，AC平分∠BAD，过C点作CE⊥AB于E，且AE=（AB+AD），则∠ABC+∠ADC=________。

04．如图36，P是等边△ABC内一点，∠APB、∠BPC、∠CPA的大小之比为5:

6:

7，则以PA、PB、PC为边的三角形三内角之比（从小到大）是________。

05．如图37，等腰△ABC中，AB=AC，∠A=20°，D是AB边上一点，AD=BC，连结CD，则∠BDC=________。

06．如图38，已知△ABC中，AC=BC，∠ACB=80°，O为△ABC内一点，∠OAB=10°，∠OBA=30°，则∠ACO=________。

07．如图39，在△ABC中，∠B=90°，M是AB上一点，使得AM＝BC，N为BC上一点，使得CN=BM，连结AN、CM相交于点P，则∠APM=________。

08．如图40，梯形ABCD中，AB∥CD，∠D=90°，M为BC上一点，且BM=MC=CD，∠DAM=50°，则∠AMC=________。

09．如图41，在四边形ABCD中,∠BAC=∠BCD=105°，∠B=∠D=45°。

若B点到直线AC的距离为101，则DA=________。

10．如图42，已知△ABC中,∠BAC=120°,以AB、AC为边分别向形外作正△ABD和正△ACE,M、N、P分别为AD、AE、BC中点,则∠MNP=_______。

二、解答题

11．如图43，在△ABC形外作等腰Rt△ABD和等腰Rt△ACE，使∠BAD、∠CAE=90°，作AH⊥BC于H，延长HA交DE于M。

求证：

DM=ME。

12．如图44，等腰△ABC中，AB=AC，∠A=100°，BE是∠ABC的平分线，求证：

AE+BE=BC。

13．如图45，在菱形ABCD中，∠BAD=120°，M、N分别为BC、CD上的点，求证：

若△AMN有一个内角等于60°，则△AMN是正三角形。

第5/5页