中考压轴一次函数注水问题Word下载.doc

中考压轴一次函数注水问题Word下载.doc

《中考压轴一次函数注水问题Word下载.doc》由会员分享，可在线阅读，更多相关《中考压轴一次函数注水问题Word下载.doc（7页珍藏版）》请在冰豆网上搜索。

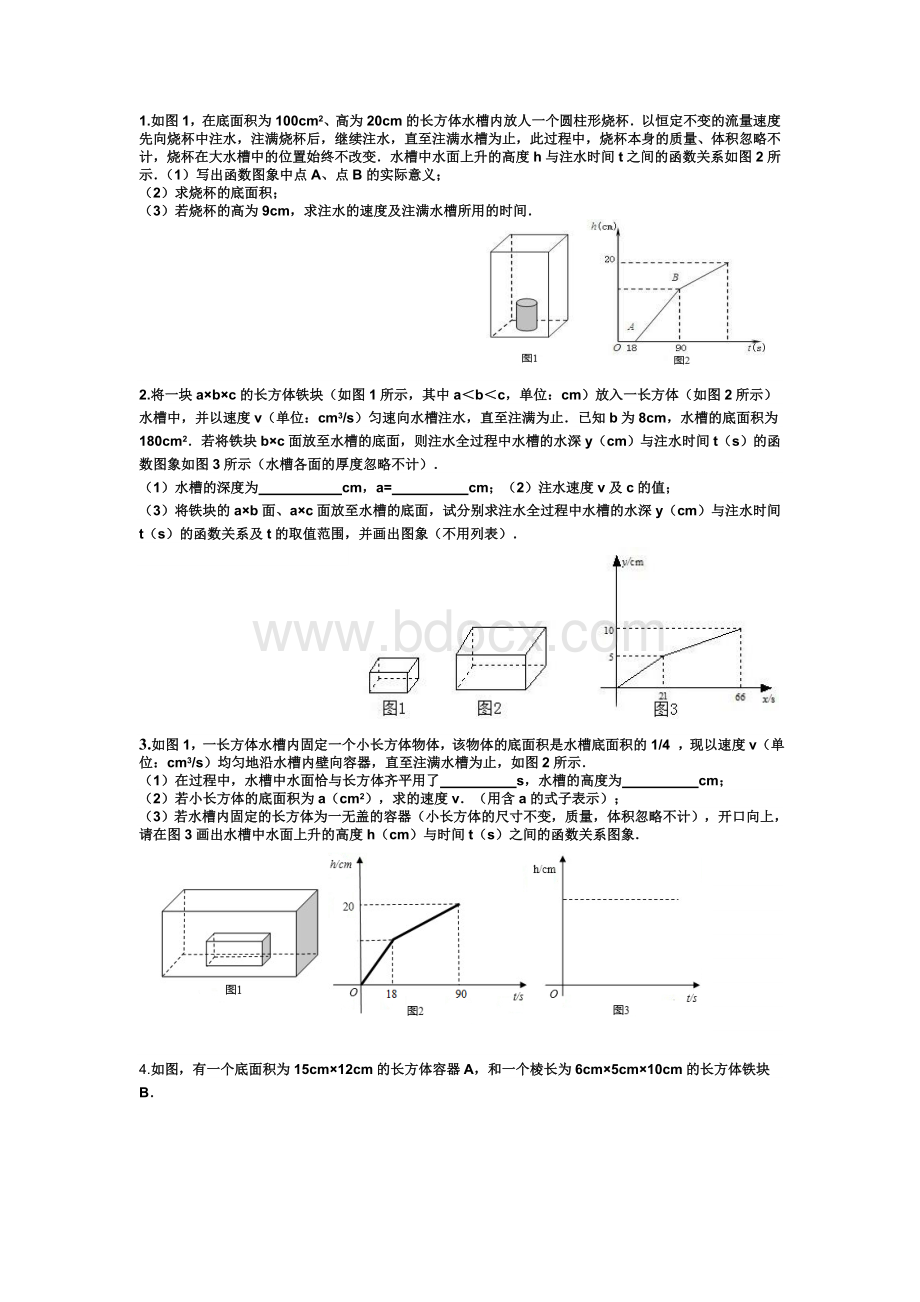
5cm×

10cm的长方体铁块B．

（1）若将铁块B的6cm×

10cm面放到容器A的底面上往A中，过程中A中水面高度y（cm）与时间x（s）的函数图象如图①所示．

①容器A的高度是cm．

②求

（1）中速度v（cm/s　）和图①中的t的值

（2）若将铁块B的6cm×

5cm面和5cm×

10cm面分别放入容器A底面，以同样速度向容器，请在图②、图③中画出水面水面高度y（cm）与时间x（s）的函数关系大致图象．

5.将一块　a　（cm）×

b　（cm　）×

c　（cm）　（a＜b＜c）的长方体铁块（如图1所示）放入一长方体水槽（如图2所示）内，铁块与水槽四壁不接触．现向水槽内匀速，直至注满水槽为止．因为铁块在水槽内有三种不同的放置方式，所以水槽内的水深h　（cm）与时间　t　（s）的函数关系用图象法来反映其全过程有三个不同的图象，如图3、4、5所示（说明：

三次速度相同）．

（1）根据图象填空

①水槽的深度是cm，a=，b=；

②t1与t2的大小关系是t1t2，并求出t1、t2的值；

（2）求水槽内的底面积和速度；

（3）求c的值．

6.将一块a（cm）×

b（cm）×

12（cm）（a＜b＜12）的长方体铁块（如图1）放入一圆柱形水槽（如图2）内，铁块与水槽侧壁不接触．现向水槽内匀速，直至注满水槽为止．在安放的过程中发现只有2种方式可以将铁块全部浸没水槽内．对这2种放法探究后发现，可用图象法（如图3、4所示）来反映水槽内的水深h（cm）与时间t（s）的函数关系．（2次速度相同）．

（1）根据图象填空：

水槽的深度为cm，a=cm，b=cm，t2=s；

（2）当24s，试计算图4方式中铁块露出水面的高度是多少？

（3）求圆柱形水槽的底面积？

7.如图1是甲、乙两个圆柱形水槽的轴截而示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）．现将甲槽中的水匀速注人乙槽，甲、乙两个水槽中水的深度y（厘米＞与时间x（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：

（1）图2中折线ABC表示

槽中水的深度与时间之间的关系，线段DE表示

槽中水的深度与时间之间的关系（以上两空选塡“甲”或“乙”），点B的纵坐标表示的实际意义是

．

（2）多长时间时，甲、乙两个水槽中水的深度相同？

（3）若乙槽底面积为36平方厘米（壁厚不计），求乙槽中铁块的体积；

（4）若乙槽中铁块的体积为112立方厘米，求甲槽底面积（壁厚不计）．（直接写成结果）

2.

（1）根据图3可知，分段函数的连接出坐标是（21，5），即21s时，水面高度是5cm，即a=5；

函数图象的末尾是（66，10），即66s时，水注满水槽，故水槽深度是10cm．

故填空依次为：

10，5（2分）

（2）由题意180×

5=5×

8×

c+21v180×

10=5×

c+66v（3分）

解得v=20，c=12

即注水速度为20cm3/s，c=12cm．（4分）

（3）①以a×

b面为底面时，

∵c=12＞10，即此时铁块高度大于水槽高度

设注满水的时间为t1s

∴180×

10+20t1解得t1=70s（5分）

∵（180-5×

8）y=20t

∴y=17t（0≤t≤70）（6分）

（画出图象）（7分）

②以a×

c面为底面时

∵b=8＜10，即此时铁块高度小于水槽高度

∴注满水时所用时间为66s（8分）

设水刚至铁块顶部的时间为t2s

8=5×

12+20t

解得t2=48（9分）

当0≤t≤48时，（180-5×

12）y=20t，即y=16t（10分）

当48＜t≤66时，180（y-8）=20（t-48），即y=19t+83

即y=16t，（0≤t≤48）19t+83．（48＜t≤66）．（11分）

（画出图象）（12分）

3.由图象可以得出18秒时水槽中水面恰与长方体齐平，

由图象可以得出90秒时水槽的高度是20厘米，

故水槽中水面恰与长方体齐平用了18s，水槽的高度是20厘米．

故答案为：

18，20．

（2）设注水时间18秒时水槽的高度设为m厘米，由题意，得

4am-amv=18①4a×

20-4amv=90-18②，

由①，得

am=6v③，

把③代入②，得

80a-24v=72v

v=56a．

（3）由题意可以知道当18分钟时注水的体积应该是小长方体体积的三倍，

则注满小长方体的时间就为18÷

3=6s，而后面注水的时间于原来相同是72s，

则注满整个水槽的时间是96s．

作图为：

4.

（1）①由函数值的最大值可得容器A的高度；

②易得如此放置时铁块B水平的容器A的容积，除以相应的时间可得注水速度，进而让铁块B上方的容积除以注水速度后加上前面时间即为t的值；

（2）铁块B的6cm×

5cm面放置于容器A中，图象是一条线段，算出剩余的容积，除以注水速度，求得时间即可；

10cm面置于容器A中，图象是分段函数，先算出到达6cm时水的体积，除以注水速度，求得时间，到达8cm时的时间和

（1）中的图象相同．解答：

解：

（1）①到8cm时，注水停止，

∴容器A的高度是8cm，

故答案为8；

②注到5cm时水的容积为：

（15×

12-6×

10）×

5=600cm3，

注水速度v=600÷

40=15cm/s；

t=40+15×

12×

3÷

15=76s；

5cm面放置于容器A中，水的容积为：

5）×

8=1200cm3，

∴注满用的时间为：

1200÷

15=80s；

10cm面置于容器A中，

注水到达6cm时水的体积为：

12-10×

6=780cm3，

780÷

15=52s；

5.

（1）①由图3、4水深到10cm以后不在增加，可知水槽深10cm，由图3可知长方体的最短棱长a的值，由图4可知处于中间的棱长b的值；

②根据水槽的容积等于长方体的体积与注入水的体积，又注入水的速度相同，所以时间t1与t2相等；

设水槽的底面积为s，根据图3图4刚好没过长方体时的注入水量表示出注入水的速度相同列式整理得到s与c的关系，然后用c表示出注入速度，再根据图3，求出注入剩下的4cm所用的时间，加上21即可得到t1的值，也就是t2的值；

（2）根据图5注入水的体积等于水槽中水的高度×

（水槽的底面积-a、b为底面的面积），计算即可求出c的值，然后再代入水槽底面积表达式与速度表达式计算即可得解；

（3）在

（2）中已求．解答：

（1）①由图3、图4可知水槽深度是10cm，

由图3知a=6cm，由图4可知b=9cm，

②前两种是完全浸没的，注水容积相同，

所以t1=t2，

设水槽底面积为s，

根据图3、4，注入水的速度为6（s-9c）21=9（s-6c）45，

整理得，10s-90c=7s-42c，

解得s=16c，

所以，注水速度为，6（s-9c）21=6（16c-9c）21=2c，

由图3，（10-6）s2c=4×

16c2c=32秒，

∴t1=21+32=53秒；

t2=t1=53秒；

①10，6cm，9cm，②=；

（2）根据图5，注入水的体积=10（s-6×

9）=62×

2c，

即10（16c-54）=124c，

解得c=15，

所以，水槽的底面积为s=16c=16×

15=240cm2，

注水速度为2c=2×

15=30cm3/s；

（3）c=15cm（上一问已求）．

6.

（1）根据已知图象，可得水槽的深度为10cm，由图3可得此时如图1放置，故高a=6cm，由图4可得此时宽作为高放置，故宽B=9cm，由两次注满的时间应相同，故t2=64s；

（2）首先求得当在0≤x≤54时的解析式，然后代入t=24，即可求得答案；

（3）设圆柱形水槽的底面积为Scm3，根据题意得：

注水速度为：

4S

40

=S

10

（cm3/s），又由6S=24S

+6×

9×

12，即可求得答案．解答：

水槽的深度为10cm，a=6cm，b=9cm，t2=64s；

根据图象可得水槽的深度为10cm，

由图3可得此时如图1放置，故高a=6cm，

由图4可得此时宽作为高放置，故宽B=9cm，

∵两次注满的时间应相同，故t2=64s；

10，6，9，64；

（2）设图4中，在0≤x≤54时的解析式为：

h=kt，

则9=54k，

解得：

k=16，

则当在0≤x≤54时的解析式为：

h=16t，

当t=24时，h=16×

24=4，

则图4方式中铁块露出水面的高度是：

9-4=5（cm）；

（3）设圆柱形水槽的底面积为Scm2，

根据题意得：

4S40=S10（cm3/s），

∴6S=24S10+6×

12，

得：

S=180．

答：

圆柱形水槽的底面积为180cm2．

7.1）乙；

水没过铁块；

（2）设线段AB、DE的解析式分别为：

y1=k1x+b，y2=k2x+b，

∵AB经过点（0，2）和（4，14），DC经过（0，12）和（6，0）

∴{4k1+b1=1

4b1=2

{b2=12

6k2+b2=0