北师大七年级下《52探索轴对称的性质》同步练习含答案Word格式.docx
《北师大七年级下《52探索轴对称的性质》同步练习含答案Word格式.docx》由会员分享,可在线阅读,更多相关《北师大七年级下《52探索轴对称的性质》同步练习含答案Word格式.docx(8页珍藏版)》请在冰豆网上搜索。
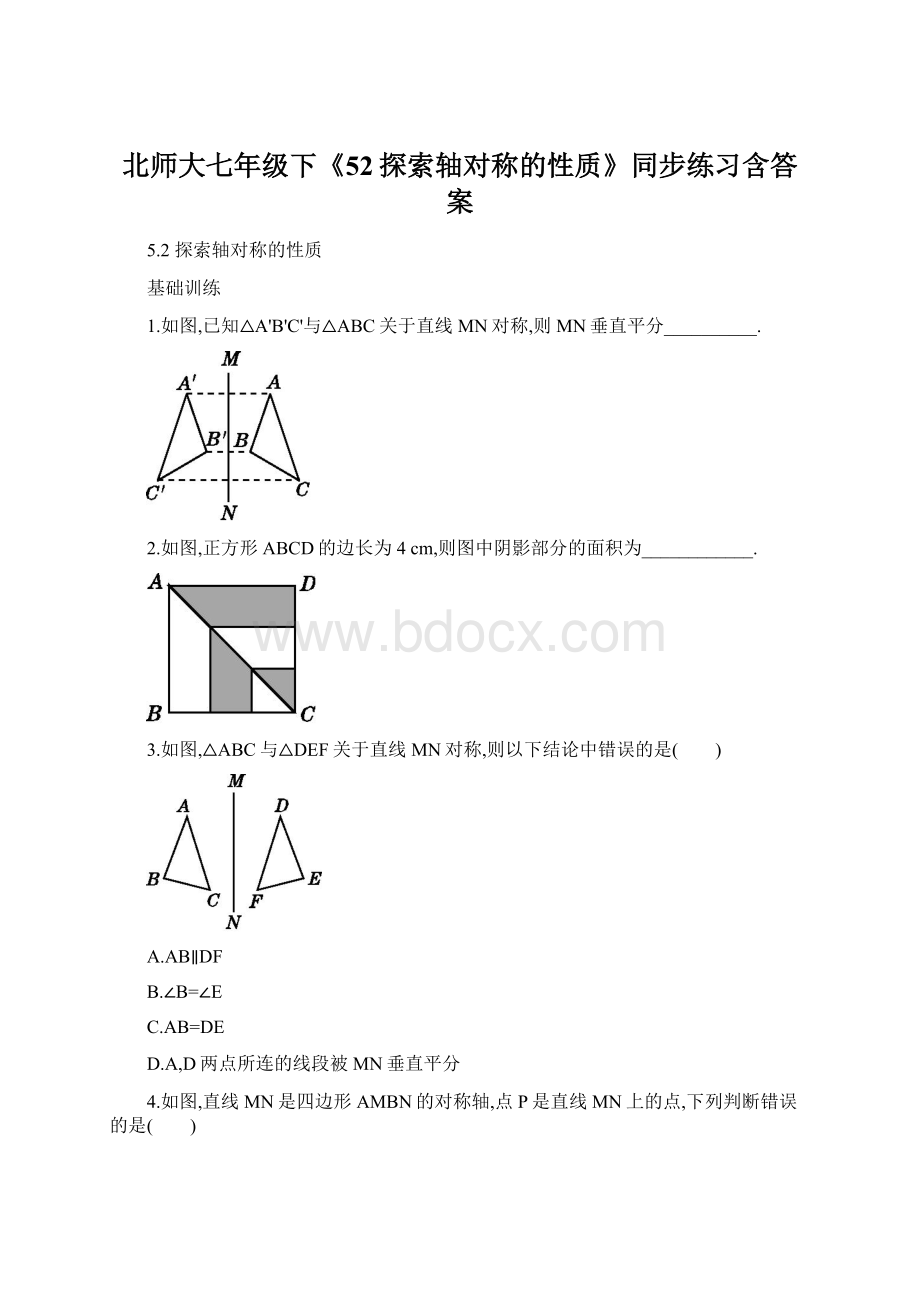
5.如图,在Rt△ABC中,∠ACB=90°
∠A<
∠B,CM=BM=AM,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30°
B.40°
C.50°
D.60°
6.如图,在△ABC中,∠ACB=90°
沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°
则∠BDC等于( )
A.44°
B.60°
C.67°
D.77°
7.如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠,使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )
A.15B.20C.25D.30
8.如图,△ABC和△A'
关于直线l对称.
(1)△ABC △A'
;
(2)A点的对应点是 ,C'
点的对应点是 ;
(3)连接BB'
交l于点M,连接AA'
交l于点N,则BM= ,AA'
与BB'
的位置关系是 ;
(4)直线l AA'
.
9.如图,在由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有 个.
10.请画出已知图形(如图所示)关于直线l的对称图形.(保留作图痕迹,不写画法)
11.如图,在2×
2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有多少个?
画出图形.
提升训练
12.如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
13.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:
△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
14.如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F.试说明:
点E,F关于AD对称.
15.如图,在△ABC中,D,E为AC边上的两个点,试在AB,BC上分别取一个点M,N,使四边形DMNE的周长最小.
16.如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'
处.
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)?
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
参考答案
1.【答案】AA'
BB'
CC'
2.【答案】8cm2 3.【答案】A
4.【答案】B
解:
因为直线MN是四边形AMBN的对称轴,
所以点A与点B对应.
所以AM=BM,AN=BN,∠ANM=∠BNM.
又因为点P是直线MN上的点,
所以∠MAP=∠MBP.故选B.
5.【答案】A
因为∠A<
∠B,AM=CM=BM,
所以∠A=∠MCA.
因为将△ACM沿CM折叠,点A落在点D处,
所以CM平分∠ACD,∠A=∠D.
所以∠ACM=∠DCM.
因为CD⊥AB,所以∠B+∠BCD=90°
.
因为∠A+∠B=90°
所以∠A=∠BCD.
所以∠BCD=∠DCM=∠MCA=30°
.所以∠A=30°
6.【答案】C
因为∠ACB=90°
∠A=22°
所以∠B=90°
-∠A=68°
由折叠知,∠BCD=∠ACD=×
90°
=45°
所以∠BDC=180°
-∠B-∠BCD=67°
7.【答案】D
由折叠知,DF=D1F,AD=A1D1=BC=5,AE=A1E.
所以阴影部分图形的周长
=A1E+EB+A1D1+FD1+FC+CB=AB+AD+DC+BC=(10+5)×
2=30.
8.【答案】
(1)≌
(2)A'
点;
C点 (3)B'
M;
互相平行 (4)垂直平分
直接由轴对称的性质得出.
9.【答案】3
10.解:
如图.
11.解:
如图,与△ABC成轴对称且也以格点为顶点的三角形有5个.
分别为△BCD,△BFH,△ADC,△AEF,△CGH.
12.解:
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
13.解:
(1)因为∠GCF+∠FCE=90°
∠FCE+∠BCE=90°
所以∠GCF=∠BCE.
又因为∠G=∠B=90°
GC=BC,
所以△FGC≌△EBC.
(2)由
(1)知,DF=GF=BE,所以四边形ECGF的面积=四边形AEFD的面积===16.
14.解:
如图,连接EF交AD于点G,
因为AD平分∠BAC,所以∠EAD=∠FAD.
又因为∠AED=∠AFD,AD=AD,
所以Rt△ADE≌Rt△ADF(AAS).
所以AE=AF.
又∠EAG=∠FAG,AG=AG,所以△AEG≌△AFG.
所以EG=FG,∠AGE=∠AGF.
又∠AGE+∠AGF=180°
所以∠AGE=∠AGF=90°
所以AD垂直平分EF.
所以点E,F关于AD对称.
15.解:
如图,
(1)作点D关于直线AB的对称点D'
作点E关于直线BC的对称点E'
.
(2)连接D'
E'
交AB于点M,交BC于点N.(3)连接DM,EN.
四边形DMNE就是符合要求的四边形,此时周长最小.
16.解:
(1)△EAD≌△EA'
D,其中∠EAD=∠EA'
D,
∠AED=∠A'
ED,∠ADE=∠A'
DE.
(2)∠1=180°
-2x,∠2=180°
-2y.
(3)∠1+∠2=360°
-2(x+y)=360°
-2(180°
-∠A)=2∠A.
规律为∠1+∠2=2∠A.