最新高考总复习数学理第二次高考模拟试题及答案解析一Word格式文档下载.docx
《最新高考总复习数学理第二次高考模拟试题及答案解析一Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《最新高考总复习数学理第二次高考模拟试题及答案解析一Word格式文档下载.docx(11页珍藏版)》请在冰豆网上搜索。
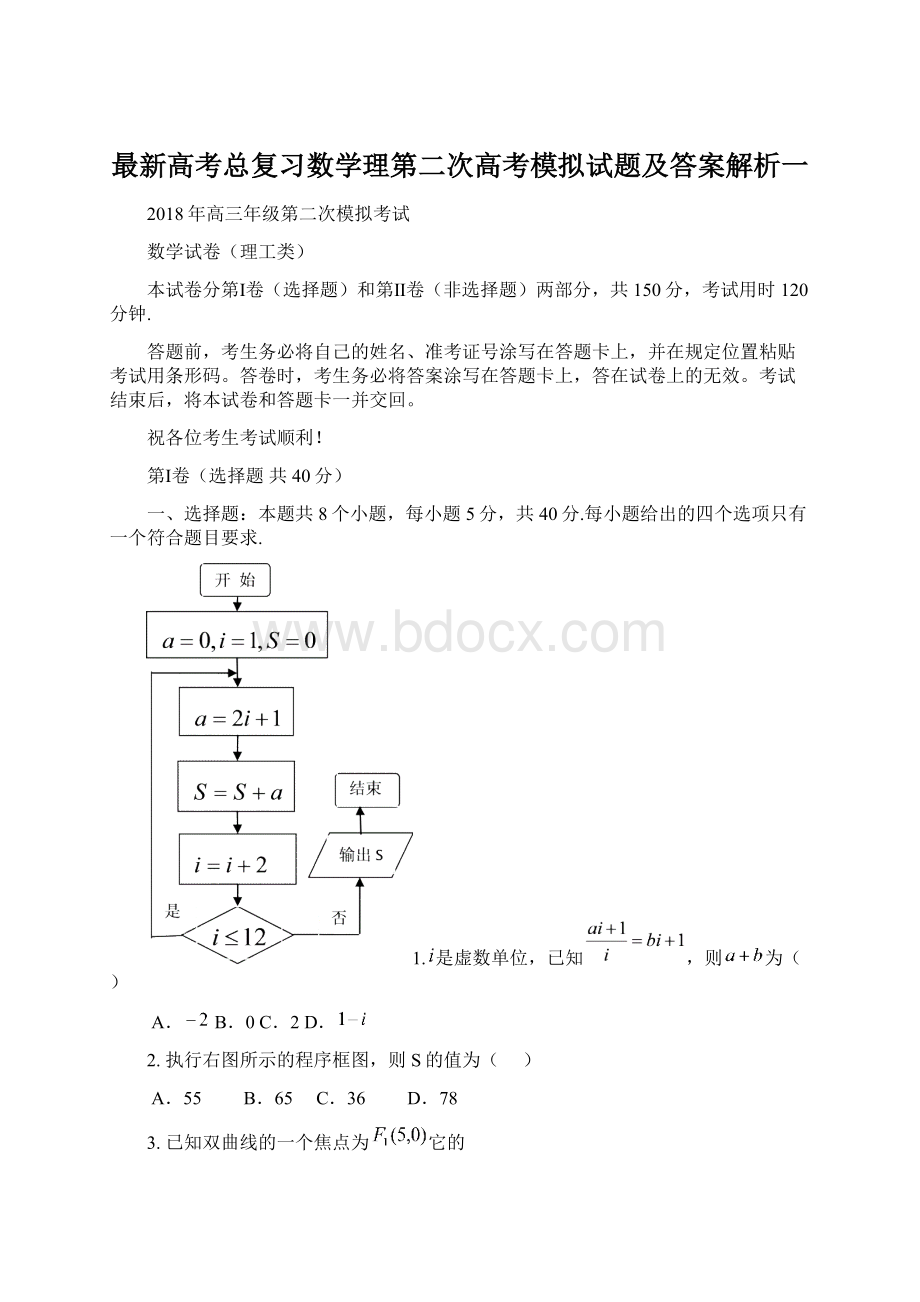
3.已知双曲线的一个焦点为它的
渐近线方程为,则该双曲线的方程为()
A.B.
C.D.
4.已知函数与,则它们的图象交点个数为()
A.0B.1 C.2D.不确定
5.“”是“点不在圆外”的什么条件()
A.充分不必要条件B.必要不充分条件
C.既不充分也不必要条件D.充要条件
6.在三角形中,的平分线为,点在边上,,,,则的值为( )
A.B.C.D.
7.如右图所示,在三角形中,,,,点为的中点,,则的长度为()
A.2B.
C.D.
8.已知,其中且,则的取值范围为()
二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)
9.某学校的学生人数为高一年级150人,高二年级180人,高三年级210人,为了调查该学校学生视力情况需要抽取72人作为样本,若采用分层抽样的方式,则高一和高二年级一共抽取的人数为________.
10.在的二项展开式
中,常数项为___________.
11.如右图所示,一款儿童玩具的
三视图中俯视图是以3为半径的圆,
则该儿童玩具的体积为______.
12.正弦曲线与直线所围成的封闭图形的面积为.
13.如右图所示,圆上的弦不为直径,
切圆于点,点在的延长线上且,
点为与圆交点,若,
则________.
14.已知函数,,若存在使,则的取值范围是____________.
三、解答题:
(本大题6个题,共80分)
15.(本小题满分13分)
已知函数
(1)求函数的最小正周期及其单调减区间;
(2)求函数在上的最大值和最小值.
16.(本小题满分13分)
某外语学校的一个社团中有7名同学,其中2人只会法语,2人只会英语,3人既会法语又会英语,现选派3人到法国的学校交流访问.
(1)在选派的3人中恰有2人会法语的概率;
(2)在选派的3人中既会法语又会英语的人数的分布列与期望.
17.(本小题满分13分)
如图四棱锥,三角形为正三角形,边长为2,,,垂直于平面于O,O为的中点,.
(1)证明;
(2)证明平面;
(3)平面与平面所成二面角的余弦值.
18.(本小题满分13分)
椭圆的右顶点为,为坐标原点,过的中点作轴的垂线与椭圆在第一象限交于点,点的纵坐标为,为半焦距.
(1)求椭圆的离心率;
(2)过点斜率为的直线与椭圆交于另一点,以为直径的圆过点P(,),求三角形的面积.
19.(本小题满分14分)
已知数列的前项和为,数列为等差数列,()
且.
(1)求、的通项公式;
(2)设,,证明:
.
20.(本小题满分14分
已知函数.
(1)求函数在处切线方程;
(2)讨论函数的单调区间;
(3)对任意,恒成立,求的范围.
数学(理)答案
本大题共8个小题,每小题5分,满分40分.
题号
1
2
3
4
5
6
7
8
答案
B
D
C
A
二、填空题:
本大题共6个小题,每小题5分,满分30分.
9.4410。
11. 12。
13.14。
本大题共6小题,满分80分.解答应写出文字说明,演算步骤或推理过程.
15、
(1)
……3分
的最小正周期为……5分
当即时为单调减函数……7分
(2)……9分
……11分最大值为,最小值为……13分
16、
(1)事件A“选派的三人中恰有2人会法语的概率为
……5分
(2)的取值为0、1、2、3,则
分布列为:
P
……13分
17、
(1)如图以A为原点建立空间直角坐标系
(0,0,0)(,-1,0)(,1,0)D(0,1,0)O(,,0)
(,,1)……2分
(,,1)
(1,,0)
(2)(,,1),(,-1,0)设平面法向量为
令,则(1,,)……7分
(,,0)平面……9分
(3)(,,1),(,0,0)
设平面法向量为
令,则(0,1,)……11分
平面与平面所成二面角的余弦值为……13分
18、
(1)由已知可知椭圆过点,代入方程有
,
,……5分
(2)点,直线
解为,由已知代入解得…11分
直线
,……13分
19、
(1)设的公差为,,,
当时,
当时,①②
由①-②得到,
由已知,解为(舍)
、的通项公式分别为……7分
(2)、
当时,,
设①②
由①-②得到
整理为
……14分
20、
(1)
切线斜率,
切线方程……4分
(2)令,即
当时,在上为增函数,在上为减函数
当时,在上为增函数,
在上为减函数
当时,在R上恒为增函数
在上为减函数……10分
(3)由已知在上的最大值小于等于
当时,在上单调递增
的最大值为
解为
的最大值为或
即
,()恒成立
即
()恒成立
当时,在上单调递减
解为成立
综上所述……14分
(注:
学生有其它解法时,请参照以上标准按步骤给分)