中考数学二次函数与abc的关系doc文档格式.docx
《中考数学二次函数与abc的关系doc文档格式.docx》由会员分享,可在线阅读,更多相关《中考数学二次函数与abc的关系doc文档格式.docx(20页珍藏版)》请在冰豆网上搜索。
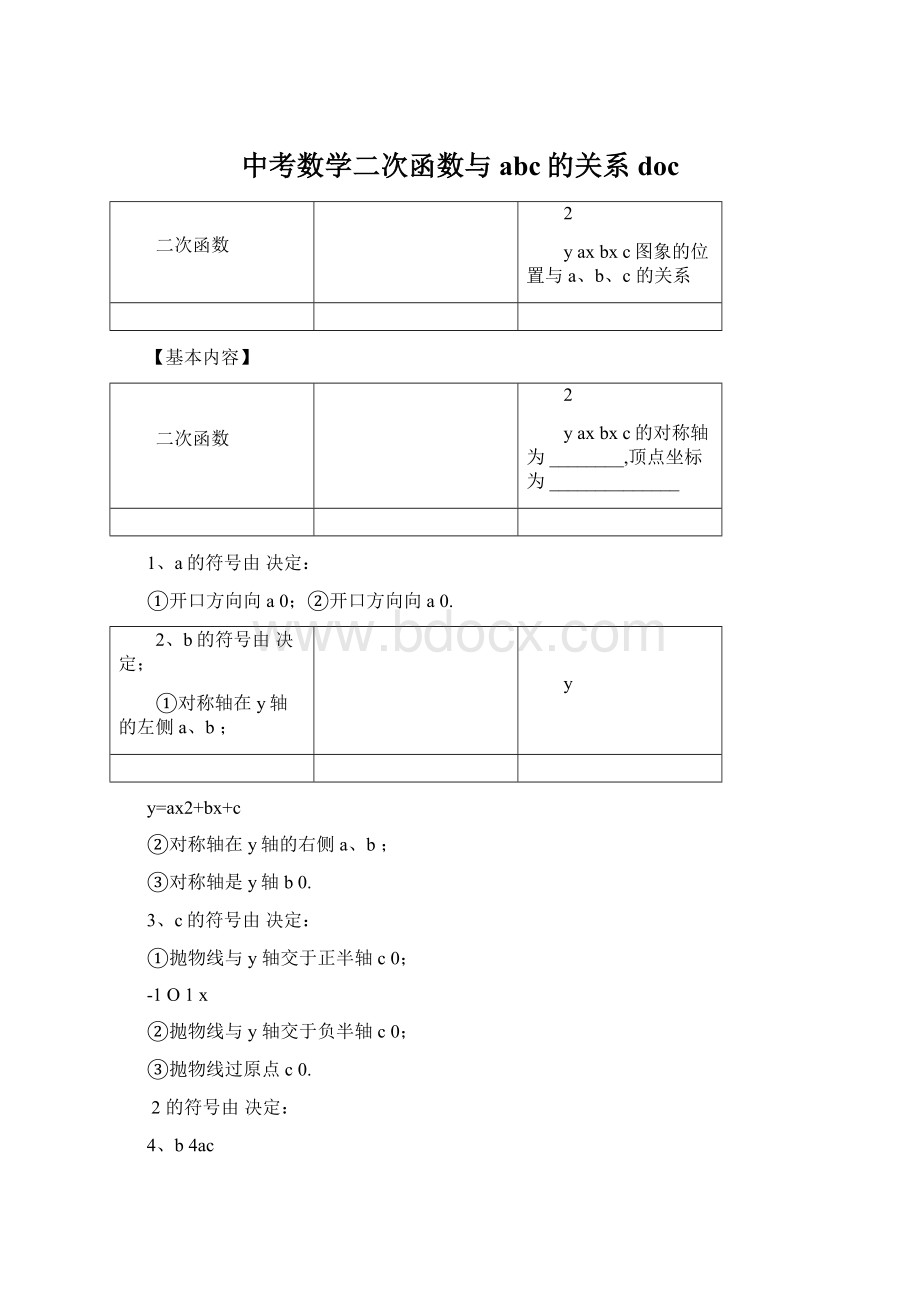
当x=-1时,y=.
二次函数的图象与性质具体如下图所示:
yyyyy
ox
ox
ooxx
xo
a0、b0a0、b0a0、b0a0、b0a0、b0a0、b0
c0、abc0c0、abc0c0、abc0c0、abc0c0、abc0c0、abc0
b
2-4ac0b2-4ac0b2-4ac0b2-4ac0b2-4ac0b2-4ac0
巩固练习:
1、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列
2+bx+c(a≠0)的图象如图所示,则下列
yx=1
4个结论中:
①abc>
0;
②b<
a+c;
③4a+2b+c>
④b
2-4ac>
⑤b=2a.正确的是(填序号)
-10x
1
2、根据图象填空,:
(1)a0,b0,c0,abc0.
2-4ac0
(2)b
(3)abc0;
abc0;
(4)当x0时,y的取值范围是;
21O1x
当y0时,x的取值范围是.
2的顶点在第二象限,交于y轴的正半轴,与x轴有两个交点,
3.若一条抛物线yaxbxc
则下列结论正确的是().
A.a﹥0,bc﹥0;
B.a﹤0,bc﹤0;
C.a﹤0,bc﹥0;
D.a﹥0,bc﹤0
4.已知二次函数y=ax
2+bx+c的图象如图所示,那么下列判断不正确的是
()
A、ac<0B、a-b+c>0C、b=-4a
D、关于x的方程ax
2+bx+c=0的根是x1=-1,x2=5
5、已知二次函数y=ax
2+bx+c(a≠0)的图象如图所示,有下列结论:
2-4ac>0;
②abc>0③8a+c>0;
④9a+3b+c<0
①b
其中,正确结论的个数是()
A、1B、2C、3D、4
6.已知反比例函数
k
y的图象在二、四象限,则二次函数
x
22
y2kxxk的图象大致为()
yy
y
Ox
OxOxOx
A.B.C.D.
7.(2014?
威海)已知二次函数y=ax
2+bx+c(a≠0)的图象如图,
则下列说法:
①c=0;
②该抛物线的对称轴是直线x=﹣1;
③当x=1时,y=2a;
④am
2+bm+a>0(m≠﹣1).
其中正确的个数是()
8.(2014?
仙游县二模)已知二次函数y=ax+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;
②a﹣b+c<0;
③b+2a<0;
④abc>0.其中所有正确结论的序号是()A.③④B.②③
C.①④D.①②③
9.(2014?
南阳二模)二次函数y=ax
+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:
﹣4ac>0;
④<0中,正确的结论有()
①a<0;
②c>0;
③b
10.(2014?
襄城区模拟)函数y=x+bx+c与y=x的图象如图,有以下结论:
﹣4c<0;
②c﹣b+1=0;
③3b+c+6=0;
④当1<x<3时,x
①b+(b﹣1)x+c<0.
其中正确结论的个数为()
A.1B.2C.3D.4
11.(2014?
宜城市模拟)如图是二次函数y=ax
下列说法:
+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0)
①abc<0;
②2a﹣b=0;
③4a+2b+c<0;
④若(﹣5,y1),(2,y2)是抛物线上的两点,则y1>y2.
其中说法正确的是()
A.①②B.②③C.②③④D.①②④
12.(2014?
莆田质检)如图,二次函数y=x+(2﹣m)x+m﹣3的图象交y轴于负半轴,对称轴在y轴的
右侧,则m的取值范围是()
A.m>2B.m<3C.m>3D.2<m<3
13.(2014?
玉林一模)如图是二次函数y=ax
+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=
﹣1.给出四个结论:
>4ac;
②2a+b=0;
③3a+c=0;
④a+b+c=0.
①b
其中正确结论的个数是()
A.1个B.2个C.3个D.4个
3
14.(2014?
乐山市中区模拟)如图,抛物线y=ax+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),
与
y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
①当x>3时,y<0;
②3a+b>0;
③﹣
1≤a≤﹣;
④≤n≤4.其中正确的是()
A.①②B.③④C.①③D.①③④
15.(2014?
齐齐哈尔二模)已知二次函数y=ax
+bx+c(a>0)的图象与x轴交于点(﹣1,0),(x1,0),
且1<x1<2,下列结论正确的个数为()①b<0;
②c<0;
③a+c<0;
④4a﹣2b+c>0.
16.(2014年四川南充)二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;
②2a+b=0;
③
2;
④a﹣b+c>0;
⑤若
当m≠1时,a+b>ambm
ax1bx=ax2bx2,且x1x2则x1x2=2.
其中正确的有()A.①②③B.②④C.②⑤D.②③⑤
17.二次函数
yxbx的图象如图,对称轴为直线x=2.若关于x的一元二次方程
xbxt0(t为实数)
在-1<x<1的范围内有解,则t的取值范围是()
A.t≥-1B.-4≤t<5
C.-1≤t<1D.-3<t<5
18.(14年泰安)二次函数y=ax+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
x-1013
y-1353
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程
210
axbxc的一个根;
210(4)当﹣1<x<3时,axbxc.
其中正确的个数为()A.4个B.3个C.2个D.1个
4
1.(2014?
威海)已知二次函数y=ax+bx+c(a≠0)的图象如图,则下列说法:
①c=0;
②该抛物线的对称轴是直线x=﹣1;
③当x=1时,y=2a;
④am+bm+a>0(m≠﹣1).
考点:
二次函数图象与系数的关系.
分析:
由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进
而对所得结论进行判断.
解答:
解:
抛物线与y轴交于原点,
c=0,(故①正确);
该抛物线的对称轴是:
,
直线x=﹣1,(故②正确);
当x=1时,y=a+b+c
∵对称轴是直线x=﹣1,
∴﹣b/2a=﹣1,b=2a,
又∵c=0,
∴y=3a,(故③错误);
x=m对应的函数值为y=am
+bm+c,
x=﹣1对应的函数值为y=a﹣b+c,
又∵x=﹣1时函数取得最小值,
∴a﹣b+c<am
+bm+c,即a﹣b<am+bm,
∵b=2a,
∴am
+bm+a>0(m≠﹣1).(故④正确).
故选:
C.
点评:
本题考查了二次函数图象与系数的关系.二次函数y=ax
+bx+c(a≠0)系数符号由抛物线开口方向、
对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.
2.(2014?
④abc>0.其中所有正确结论的序号是()
A.③④B.②③C.①④D.①②③
专题:
数形结合.
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物
线与x轴交点情况进行推理,进而对所得结论进行判断.
①当x=1时,y=a+b+c=0,故①错误;
②当x=﹣1时,图象与x轴交点负半轴明显大于﹣1,
∴y=a﹣b+c<0,
故②正确;
③由抛物线的开口向下知a<0,
∵对称轴为0<x=﹣<1,
∴2a+b<0,
5
故③正确;
④对称轴为x=﹣>0,a<0
∴a、b异号,即b>0,
由图知抛物线与y轴交于正半轴,∴c>0
∴abc<0,
故④错误;
∴正确结论的序号为②③.
B.
二次函数y=ax
+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:
开口方向向上,则a>0;
否则a<0;
(2)b由对称轴和a的符号确定:
由对称轴公式x=﹣判断符号;
(3)c由抛物线与y轴的交点确定:
交点在y轴正