陕西省榆林市届高考数学上学期第一次模拟测试试题理含答案Word文档下载推荐.docx

陕西省榆林市届高考数学上学期第一次模拟测试试题理含答案Word文档下载推荐.docx

《陕西省榆林市届高考数学上学期第一次模拟测试试题理含答案Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《陕西省榆林市届高考数学上学期第一次模拟测试试题理含答案Word文档下载推荐.docx（26页珍藏版）》请在冰豆网上搜索。

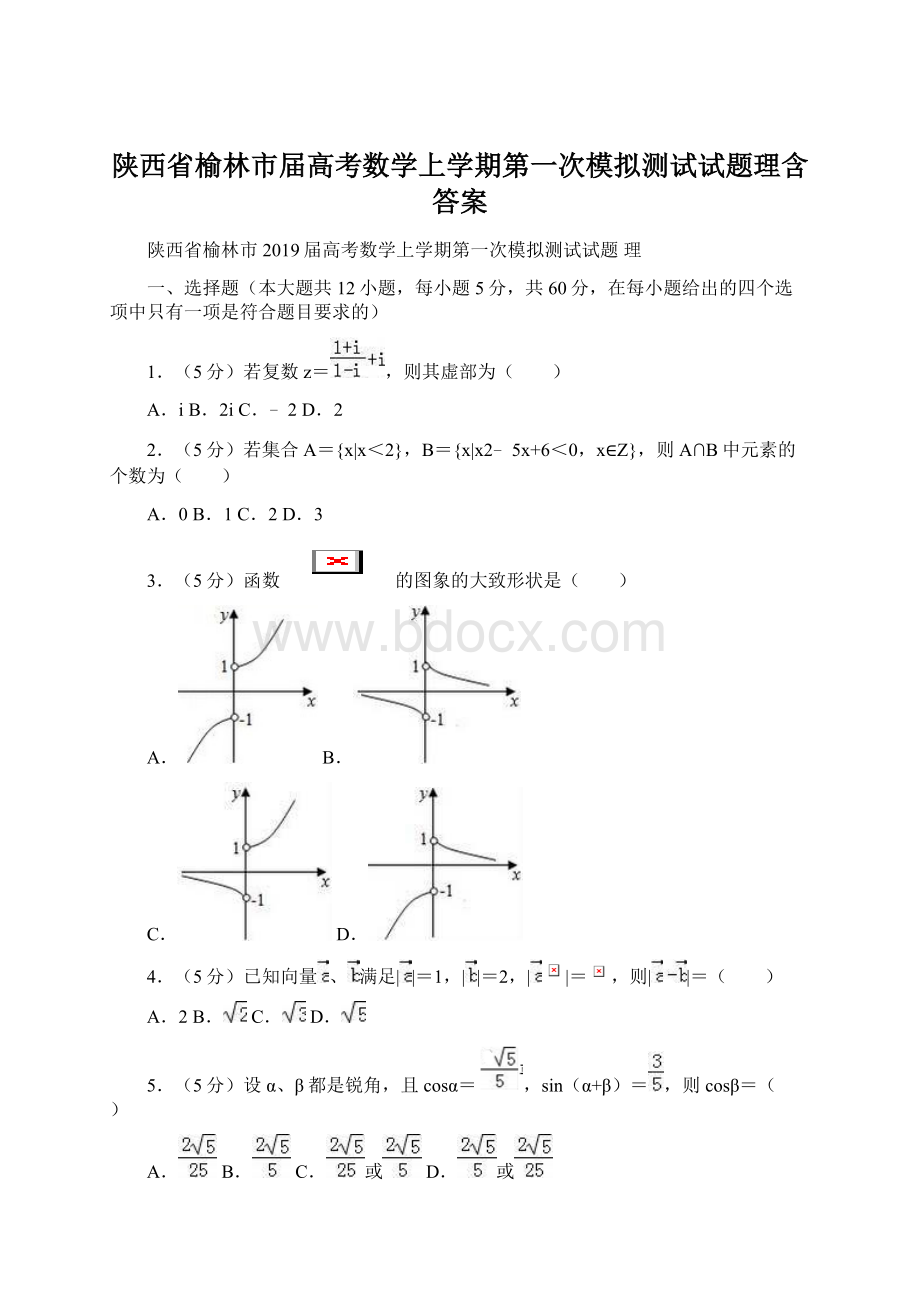
6．（5分）设x，y满足约束条件，则Z＝3x﹣2y的最大值是（　　）

A．0B．2C．4D．6

7．（5分）《九章算术》是我国古代数学文化的优秀遗产，数学家刘徽在注解《九章算术》时，发现当圆内接正多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，为此他创立了割圆术，利用割圆术，刘徽得到了圆周率精确到小数点后四位3.1416，后人称3.14为徽率．如图是利用刘徽的割圆术设计的程序框图，若结束程序时，则输出的n为（　　）（≈1.732，sin15°

≈0.258，sin7.5°

≈0.131）

A．6B．12C．24D．48

8．（5分）如图所示，在正方体ABCD﹣A1B1C1D1中，若点E为BC的中点，点F为B1C1的中点，则异面直线AF与C1E所成角的余弦值为（　　）

9．（5分）在等比数列{an}中，a1+an＝34，a2•an﹣1＝64，且前n项和Sn＝62，则项数n等于（　　）

A．4B．5C．6D．7

10．（5分）已知定义域为R的偶函数f（x）在（﹣∞，0]上是减函数，且＝2，则不等式f（log4x）＞2的解集为（　　）

A．B．（2，+∞）

11．（5分）设f（x）＝x3+log2（x+），则对任意实数a、b，若a+b≥0，则（　　）

A．f（a）+f（b）≤0B．f（a）+f（b）≥0

C．f（a）﹣f（b）≤0D．f（a）﹣f（b）≥0

12．（5分）已知F1，F2分别为双曲线C：

﹣＝1（a＞0，b＞0）的左、右焦点，过F1的直线l与双曲线C的左右两支分别交于A，B两点，若|AB|：

|BF2|：

|AF2|＝3：

4：

5，则双曲线的离心率为（　　）

A．B．C．2D．

二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题纸中相应的機线上）

13．（5分）我国南宋著名数学家秦九韶发现了从三角形三边求三角形面积的“三斜公式”，设△ABC三个内角A、B、C所对的边分别为a、b、c，面积为S，则“三斜求积”公式为．若a2sinC＝4sinA，（a+c）2＝12+b2，则用“三斜求积”公式求得△ABC的面积为　　．

14．（5分）已知函数f（x）＝﹣+4x﹣3lnx在[t，t+1]上不单调，则t的取值范围是　　．

15．（5分）已知不等式ex﹣1≥kx+lnx，对于任意的x∈（0，+∞）恒成立，则k的最大值　　

16．（5分）已知G为△ABC的重心，过点G的直线与边AB，AC分别相交于点P，Q，若AP＝λAB，则当△ABC与△APQ的面积之比为时，实数λ的值为　　．

三、解答题（本大题共5小题，共70分，解答应写出文字说明、证明过程或演算步骤第17-21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答）

17．（12分）已知数列{an}中，a1＝4，an＞0，前n项和为Sn，若an＝+，（n∈N*，n≥2）．

（l）求数列{an}的通项公式；

（2）若数列{}前n项和为Tn，求证

18．（12分）在△ABC中，角A、B、C的对边分别为a、b、c，且（2a﹣c）（a2﹣b2+c2）＝2abccosC．

（1）求角B的大小；

（2）若sinA+1﹣（cosC）＝0，求的值．

19．（12分）设椭圆C：

的离心率e＝，左顶点M到直线＝1的距离d＝，O为坐标原点．

（Ⅰ）求椭圆C的方程；

（Ⅱ）设直线l与椭圆C相交于A，B两点，若以AB为直径的圆经过坐标原点，证明：

点O到直线AB的距离为定值；

（Ⅲ）在（Ⅱ）的条件下，试求△AOB的面积S的最小值．

20．（12分）如图，四棱锥P﹣ABCD的底面ABCD为平行四边形，DA＝DP，BA＝BP．

（1）求证：

PA⊥BD；

（2）若DA⊥DP，∠ABP＝60°

，BA＝BP＝BD＝2，求二面角D﹣PC﹣B的正弦值．

21．（12分）已知函数f（x）＝x2﹣2．

（1）已知函数g（x）＝f（x）+2（x+1）+alnx在区间（0，1）上单调，求实数a的取值范围；

（2）函数有几个零点？

[选修4-4：

坐标系与参数方程选讲]

22．（10分）已知曲线C的参数方程为（α为参数），设直线l的极坐标方程为4ρcosθ+3ρsinθ﹣8＝0．

（1）将曲线C的参数方程化为普通方程．并指出其曲线是什么曲线．

（2）设直线1与x轴的交点为P，Q为曲线C上一动点，求PQ的最大值．

[选修4-5：

不等式选讲]

23．设函数f（x）＝|x+1|+|x﹣a|（a＞0）．

（1）作出函数f（x）的图象；

（2）若不等式f（x）≥5的解集为（﹣∞，﹣2]∪[3，+∞），求a值．

2019年陕西省榆林市高考数学一模试卷（理科）

参考答案与试题解析

【分析】直接利用复数代数形式的乘除运算化简得答案．

【解答】解：

∵z＝＝，

∴z的虚部为2．

故选：

D．

【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．

【分析】化简集合B，根据交集的定义写出A∩B，再判断其中元素个数．

集合A＝{x|x＜2}，B＝{x|x2﹣5x+6＜0，x∈Z}＝{x|2＜x＜3，x∈Z}＝∅，

则A∩B＝∅，其中元素的个数为0．

A．

【点评】本题考查了集合的化简与运算问题，是基础题．

【分析】f（x）中含有|x|，故f（x）是分段函数，根据x的正负写出分段函数的解析式，对照图象选择即可．

f（x）是分段函数，根据x的正负写出分段函数的解析式，f（x）＝，

∴x＞0时，图象与y＝ax在第一象限的图象一样，x＜0时，图象与y＝ax的图象关于x轴对称，

C．

【点评】本题考查识图问题，利用特值或转化为比较熟悉的函数，利用图象变换或利用函数的性质是识图问题常用的方法．

【分析】运用向量模长的计算可得结果．

根据题意得，（﹣）2＝2+2﹣2•

又（+）2＝2+2•+2＝1+4+2•＝6

∴2•＝1，

∴（﹣）2＝1+4﹣1＝4，

∴＝2．

【点评】本题考查向量模长的计算．

【分析】由α、β都是锐角，且cosα值小于，得到sinα大于0，利用余弦函数的图象与性质得出α的范围，再由sin（α+β）的值大于，利用正弦函数的图象与性质得出α+β为钝角，可得出cos（α+β）小于0，然后利用同角三角函数间的基本关系分别求出sinα和cos（α+β）的值，将所求式子中的角β变形为（α+β）﹣α，利用两角和与差的余弦函数公式化简后，把各自的值代入即可求出值．

∵α、β都是锐角，且cosα＝，

∴cos（α+β）＝﹣＝﹣，sinα＝＝，

则cosβ＝cos[（α+β）﹣α]＝cos（α+β）cosα+sin（α+β）sinα＝

＝．

【点评】此题考查了同角三角函数间的基本关系，正弦、余弦函数的图象与性质，以及两角和与差的余弦函数公式，熟练掌握公式及基本关系是解本题的关键．

【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，求得最优解的坐标，代入目标函数得答案．

由约束条件作出可行域如图，

化目标函数Z＝3x﹣2y为，

由图可知，当直线过A（0，﹣2）时，直线在y轴上的截距最小，

z有最大值为3×

0﹣2×

（﹣2）＝4．

【点评】本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．

【分析】列出循环过程中s与n的数值，满足判断框的条件即可结束循环．

模拟执行程序，可得：

n＝3，S＝3×

sin120°

＝，

不满足条件S＞3，执行循环体，n＝6，S＝6×

sin60°

不满足条件S＞3，执行循环体，n＝12，S＝×

12×

sin30°

＝3，

不满足条件S＞3，执行循环体，n＝24，S＝×

24×

sin15°

≈12×

0.2588＝3.1056，

满足条件S＞3，退出循环，输出n的值为24．

【点评】本题考查循环框图的应用，考查了计算能力，注意判断框的条件的应用，属于基础题．

【分析】以A为原点，AB为x轴，AD为y轴，AA1为z轴，建立空间直角坐标系，利用向量法能求出异面直线AF与C1E所成角的余弦值．

以A为原点，AB为x轴，AD为y轴，AA1为z轴，建立空间直角坐标系，

设正方体ABCD﹣A1B1C1D1中，棱长为2，

则A（0，0，0），F（2，1，2），C1（2，2，2），

E（2，1，0），

＝（2，1，2），＝（0，﹣1，﹣2），

设异面直线AF与C1E所成角为θ，

则cosθ＝＝＝，

∴异面直线AF与C1E所成角的余弦值为

B．

【点评】本题考查异面直线所成角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．

【分析】根据等比数列的性质得到a2•an﹣1＝a1•an＝64，与已知的a1+an＝34联立，即可求出a1与an的值，然后利用等比数列的前n项和公式表示出Sn，把求出的a1与an的值代入即可求出公比q的值，根据an的值，利用等比数列的通项公式即可求出项数n的值．

【