Apriori算法及java实现Word下载.docx
《Apriori算法及java实现Word下载.docx》由会员分享,可在线阅读,更多相关《Apriori算法及java实现Word下载.docx(11页珍藏版)》请在冰豆网上搜索。
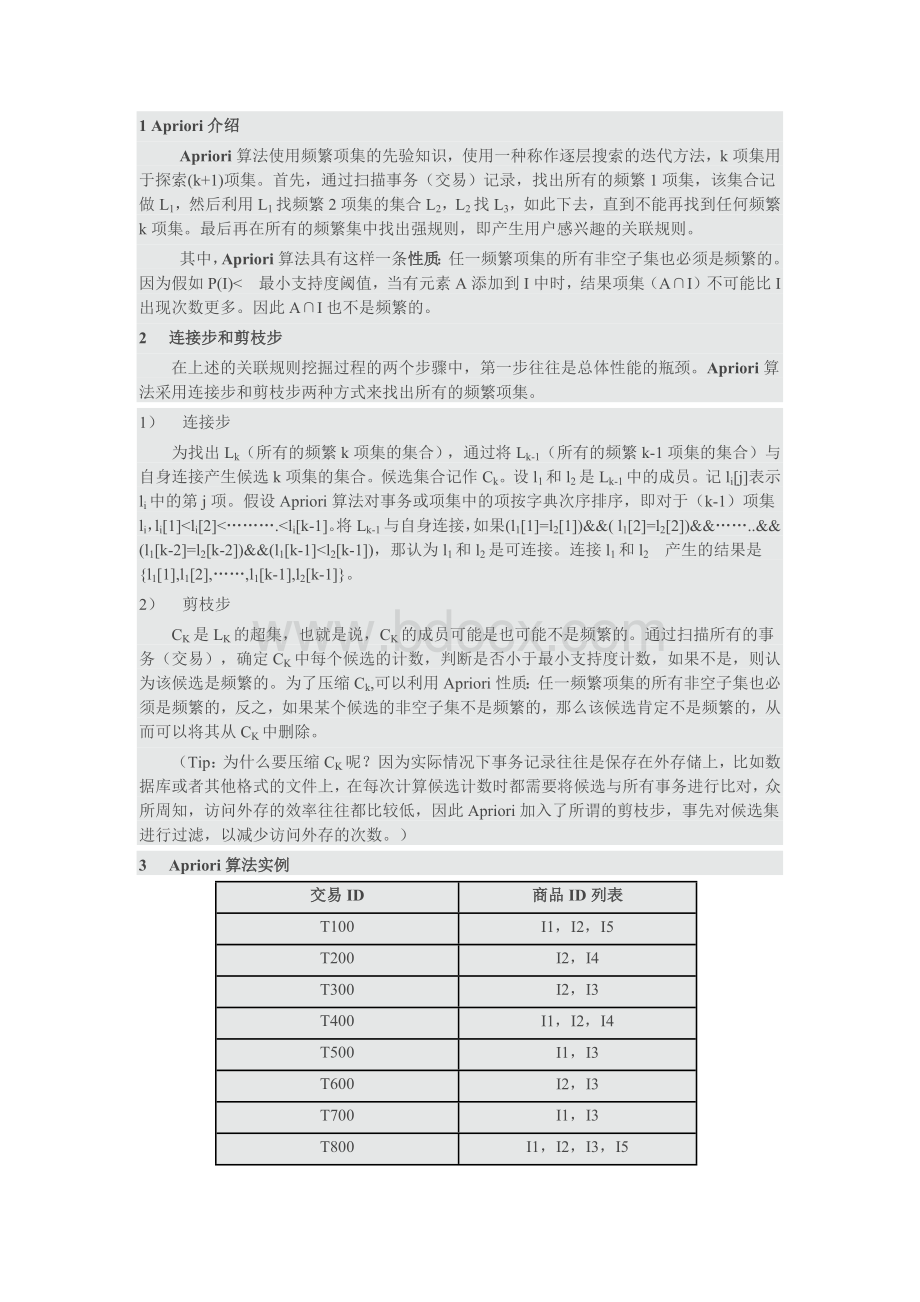
li[2]<
……….<
li[k-1]。
将Lk-1与自身连接,如果(l1[1]=l2[1])&
&
(l1[2]=l2[2])&
……..&
(l1[k-2]=l2[k-2])&
(l1[k-1]<
l2[k-1]),那认为l1和l2是可连接。
连接l1和l2
产生的结果是{l1[1],l1[2],……,l1[k-1],l2[k-1]}。
2)
剪枝步
CK是LK的超集,也就是说,CK的成员可能是也可能不是频繁的。
通过扫描所有的事务(交易),确定CK中每个候选的计数,判断是否小于最小支持度计数,如果不是,则认为该候选是频繁的。
为了压缩Ck,可以利用Apriori性质:
任一频繁项集的所有非空子集也必须是频繁的,反之,如果某个候选的非空子集不是频繁的,那么该候选肯定不是频繁的,从而可以将其从CK中删除。
(Tip:
为什么要压缩CK呢?
因为实际情况下事务记录往往是保存在外存储上,比如数据库或者其他格式的文件上,在每次计算候选计数时都需要将候选与所有事务进行比对,众所周知,访问外存的效率往往都比较低,因此Apriori加入了所谓的剪枝步,事先对候选集进行过滤,以减少访问外存的次数。
)
3
Apriori算法实例
交易ID
商品ID列表
T100
I1,I2,I5
T200
I2,I4
T300
I2,I3
T400
I1,I2,I4
T500
I1,I3
T600
T700
T800
I1,I2,I3,I5
T900
I1,I2,I3
上图为某商场的交易记录,共有9个事务,利用Apriori算法寻找所有的频繁项集的过程如下:
详细介绍下候选3项集的集合C3的产生过程:
从连接步,首先C3={{I1,I2,I3},{I1,I2,I5},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}(C3是由L2与自身连接产生)。
根据Apriori性质,频繁项集的所有子集也必须频繁的,可以确定有4个候选集{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}}不可能时频繁的,因为它们存在子集不属于频繁集,因此将它们从C3中删除。
注意,由于Apriori算法使用逐层搜索技术,给定候选k项集后,只需检查它们的(k-1)个子集是否频繁。
3.
Apriori伪代码
算法:
Apriori
输入:
D-
事务数据库;
min_sup-
最小支持度计数阈值
输出:
L-D中的频繁项集
方法:
L1=find_frequent_1-itemsets(D);
//
找出所有频繁1项集
For(k=2;
Lk-1!
=null;
k++){
Ck=apriori_gen(Lk-1);
产生候选,并剪枝
Foreach
事务tinD{//
扫描D进行候选计数
Ct
=subset(Ck,t);
得到t的子集
候选c
属于
Ct
c.count++;
}
Lk={c属于Ck
|c.count>
=min_sup}
ReturnL=所有的频繁集;
Procedureapriori_gen(Lk-1:
frequent(k-1)-itemsets)
Foreach项集l1属于Lk-1
Foreach项集
l2属于Lk-1
If((l1[1]=l2[1])&
……..
l2[k-1]))then{
c=l1连接l2
//连接步:
产生候选
ifhas_infrequent_subset(c,Lk-1)then
deletec;
//剪枝步:
删除非频繁候选
elseaddctoCk;
ReturnCk;
Procedurehas_infrequent_sub(c:
candidatek-itemset;
Lk-1:
Foreach(k-1)-subsetsofc
Ifs不属于Lk-1
then
Returntrue;
Returnfalse;
4.
由频繁项集产生关联规则
Confidence(A->
B)=P(B|A)=support_count(AB)/support_count(A)
关联规则产生步骤如下:
对于每个频繁项集l,产生其所有非空真子集;
对于每个非空真子集s,如果support_count(l)/support_count(s)>
=min_conf,则输出
s->
(l-s),其中,min_conf是最小置信度阈值。
例如,在上述例子中,针对频繁集{I1,I2,I5}。
可以产生哪些关联规则?
该频繁集的非空真子集有{I1,I2},{I1,I5},{I2,I5},{I1},{I2}和{I5},对应置信度如下:
I1&
I2->
I5
confidence=2/4=50%
I5->
I2
confidence=2/2=100%
I2&
I1
I1->
confidence=2/6=33%
I2->
confidence=2/7=29%
I5->
如果min_conf=70%,则强规则有I1&
I2,I2&
I1,I5->
I2。
5.
AprioriJava代码
packagecom.apriori;
importjava.util.ArrayList;
importjava.util.Collections;
importjava.util.HashMap;
importjava.util.List;
importjava.util.Map;
importjava.util.Set;
publicclassApriori{
privatefinalstaticintSUPPORT=2;
支持度阈值
privatefinalstaticdoubleCONFIDENCE=0.7;
置信度阈值
privatefinalstaticStringITEM_SPLIT="
;
"
项之间的分隔符
privatefinalstaticStringCON="
->
privatefinalstaticList<
String>
transList=newArrayList<
();
//所有交易
static{//初始化交易记录
transList.add("
1;
2;
5;
);
4;
3;
publicMap<
String,Integer>
getFC(){
Map<
frequentCollectionMap=newHashMap<
//所有的频繁集
frequentCollectionMap.putAll(getItem1FC());
itemkFcMap=newHashMap<
itemkFcMap.putAll(getItem1FC());
while(itemkFcMap!
=null&
itemkFcMap.size()!
=0){
candidateCollection=getCandidateCollection(itemkFcMap);
Set<
ccKeySet=candidateCollection.keySet();
//对候选集项进行累加计数
for(Stringtrans:
transList){
for(Stringcandidate:
ccKeySet){
booleanflag=true;
//
用来判断交易中是否出现该候选项,如果出现,计数加1
String[]candidateIte