实验九 信号的自然采样与恢复Word文档下载推荐.docx

实验九 信号的自然采样与恢复Word文档下载推荐.docx

《实验九 信号的自然采样与恢复Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《实验九 信号的自然采样与恢复Word文档下载推荐.docx（24页珍藏版）》请在冰豆网上搜索。

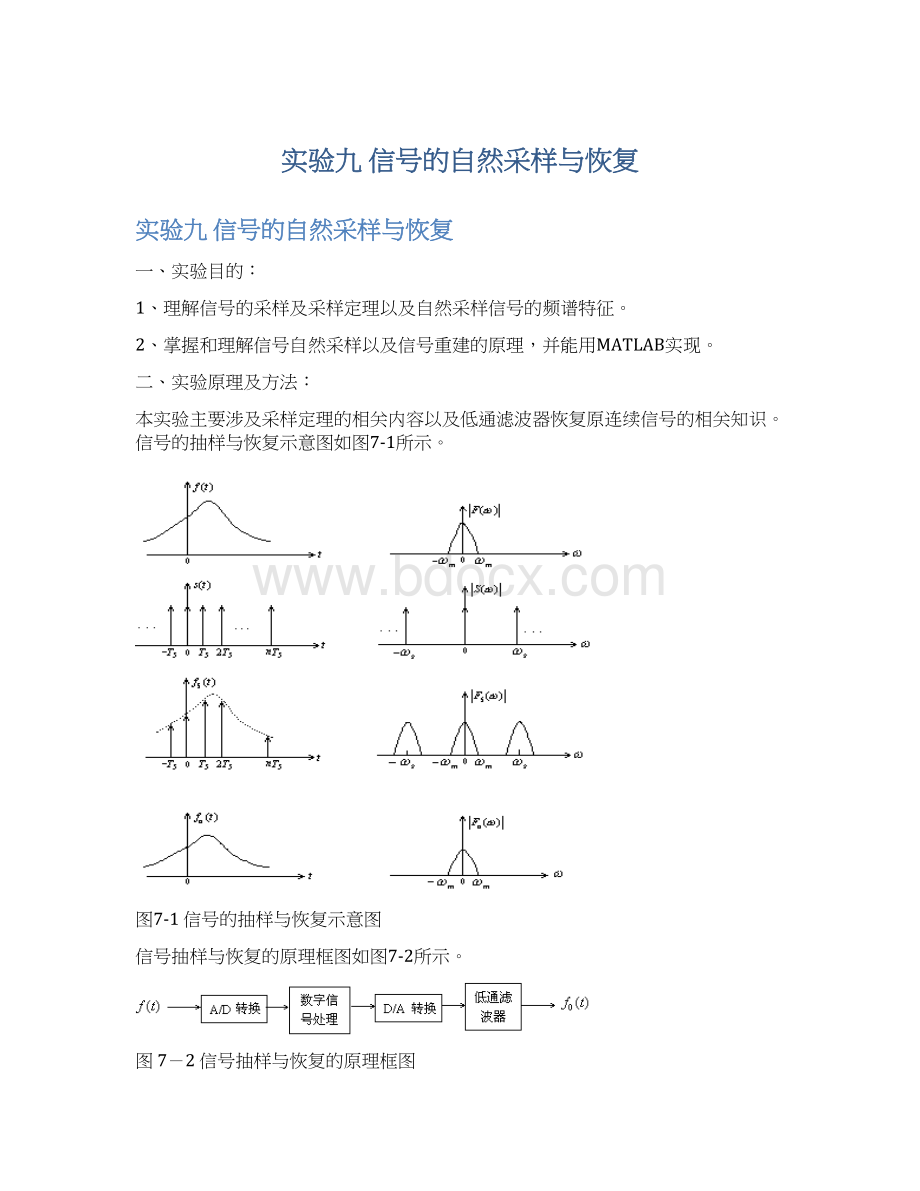
给定带限信号f（t），其频谱为

1、画出此信号的频谱图（ω的取值：

-0.5π<

ω<

0.5π，精度取0.01rad）。

答：

画出f（t）的频谱图即F（W）的图像

程序代码如下：

#include<

stdio.h>

math.h>

#definePI3.14

doublef（doublew）

{

if（w>

=-0.5*PI&

&

w<

=0.5*PI）

returncos（w）;

elsereturn0;

}

main（）

doublew,F;

FILE*fp;

for（w=-0.5*PI;

w<

=0.5*PI;

w+=0.01）

{

F=f（w）;

printf（"

w=%.2f,F（w）=%f\n"

w,F）;

fp=fopen（"

d:

\\2.txt"

"

w"

）;

fprintf（fp,"

%f\t"

F）;

}

system（"

pause"

③F（W）的图像

2、对此频域信号进行傅里叶逆变换，得到相应的时域信号，画出此信号的时域波形f（t）（t的取值：

-20s<

t<

20s；

精度取0.1s）。

对此频域信号进行傅里叶逆变换，得到相应的时域信号，画出此信号的时域波形f（t）

#include<

doublef（doublet）

doublew=-0.5*PI,f=0;

doubleans;

while（w<

f=f+cos（w）*cos（w*t）*0.01;

w=w+0.01;

ans=f/（2*PI）;

returnans;

}

doublet,ans=0;

for（t=-20;

20;

t+=0.1）

ans=f（t）;

t=%.1f,f（t）=%f\n"

t,ans）;

将实验数据导入matlab，对数据进行仿真绘图。

3分别用三种不同抽样频率f=0.2Hz,0.5Hz,1.0Hz的周期矩形脉冲信号（矩形脉冲的幅度E取1，宽度τ取0.01s）对f（t）进行抽样，画出抽样后的信号的频谱图（ω的取值：

-10rad<

ω<

10rad，精度取0.01rad）。

三种不同频率的抽样

分别用三种不同抽样频率f=0.2Hz,0.5Hz,1.0Hz的周期矩形脉冲信号（矩形脉冲的幅度E取1，宽度τ取0.01s）对f（t）进行抽样，画出抽样后的信号的频谱图

#defineINF2000

doublesa（doublex）

if（x==0）return1;

elsereturnsin（x）/x;

doublef1（doublew）

if（w>

returncos（w）;

elsereturn0;

doublef2（doublew,doublef）

doubles=0,ans;

intn;

for（n=-INF;

n<

=INF;

n+=1）

s=s+f1（w-n*2*PI*f）*sa（n*2*PI*f*0.01/2）;

ans=s*0.01*f;

returnans;

doublew,fs=0,f;

f=0.25;

/*0.2,0.5,1*/

for（w=-10;

=10;

w+=0.1）

fs=f2（w,f）;

w=%.2f,Fs（w）=%f\n"

w,fs）;

③不同抽样频率下的频谱图：

f=0.2Hz

f=0.5Hz

f=1.0Hz

4针对3中抽样所得的矩形抽样信号，用滤波器

对所得信号进行滤波，所得恢复信号f（t）的频谱记为F‘（w），与原信号的频谱F（w）进行比较（ω的取值：

-2rad<

2rad，精度取0.01rad）。

将恢复信号的频谱图与原信号的频谱图进行比较

①程序代码如下：

#definePI3.14

#defineINF2000

{

if（x==0）return1;

elsereturnsin（x）/x;

elsereturn0;

doubles=0,ans;

intn;

for（n=-INF;

s=s+f1（w-n*2*PI*f）*sa（n*2*PI*f*0.01/2）;

ans=s;

f=0.2;

for（w=-2;

=2;

if（w>

-0.5*PI&

0.5*PI）fs=f2（w,f）;

elsefs=0;

w=%.2f,Fs'

（w）=%f\t"

②恢复信号与原始信号比较

原始信号频谱：

抽样频率为0.2Hz恢复信号的频谱：

抽样频率为0.5Hz恢复信号的频谱：

抽样频率为1.0Hz恢复信号的频谱：

根据抽样定理ωm≥2ωc，要想获得完整的原信号的波形，最小抽样频率为0.5Hz。

通过将恢复信号频谱图与原信号的频谱图进行比较可得：

当抽样频率为0.2Hz时恢复信号的频谱图与原信号的频谱图相差很多，无法从抽样信号中获得原信号的完整波形；

当抽样频率为0.5Hz和1.0Hz时，恢复信号的频谱图与原信号频谱图非常接近，也就是可以从抽样信号中获得原信号波形。

因此，实验结果与理论推导出的结果一样，从而验证了抽样定理。

5、从时域比较原信号和采样恢复的信号，找出区别并说明原因。

分析：

恢复曲线与原信号曲线基本相同，说明恢复误差很小，如果采样频率减小，误差增大，采样频率增大，则恢复误差更小。

采样频率应遵循乃奎斯特定理。

实验十二FDMA通信系统的设计

1、加深对调制与解调原理及过程的理解，能将调制与解调原理应用到FDMA通信系统中；

2、加深对滤波器滤波特性的理解。

3、掌握FDMA通信系统的原理，并利用Matlab进行实现。

1、频分复用的原理

复用是指将若干个彼此独立的信号合并成可在同一信道上传输的复合信号的方法，常见的信号复用采用按频率区分与按时间区分的方式，前者称为频分复用，后者称为时分复用。

通常在通信系统中，信道所提供的带宽往往比传输一路信号所需要的带宽宽得多，这样就可以将信道的带宽分割成不同的频段，每频段传输一路信号，这就是频分复用（frequencydivisionmultipleaccess）（FDMA）。

为此，在发送端首先要对各路信号进行调制将其频谱函数搬移到相应的频段内，使之互不重叠。

再送入信道一并传输。

在接收端则采用不同通带的带通滤波器将各路信号分隔，然后再分别解调，恢复各路信号。

调制的方式可以任意选择，但常用的是单边带调制。

因为每一路信号占据的频段小，最节省频带，在同一信道中传送的路数可以增加。

图1频分复用系统的示意图

图1给出了频分复用系统的示意图。

如图所示，其中f1（t）,f2（t）,…,fn（t）为n路低频信号，通过调制器形成各路处于不同频段上的边带信号。

频分复用的理论基础仍然是调制和解调。

通常为防止邻路信号的相互干扰，相邻两路间还要留有防护频带，因此各路载频之间的间隔应为每路信号的频带与保护频带之和。

以语音信号为例，其频谱一般在0.3~3.4kHz范围内，防护频带标准为900Hz，则每路信号占据频带为4.3kHz，以此来选择相应的各路载频频率，在接收端则用带通滤波器将各路信号分离再经同步检波即可恢复各路信号，为减少载波频率的类型，有时也用二次调制。

频分复用技术除传统意义上的频分复用（FDMA）外，还有一种是正交频分复用（OFDM）。

（1）传统的频分复用

传统的频分复用典型的应用莫过于广电HFC网络电视信号的传输了，不管是模拟电视信号还是数字电视信号都是如此，因为对于数字电视信号而言，尽管在每一个频道（8MHz）以内是时分复用传输的，但各个频道之间仍然是以频分复用的方式传输的。

（2）正交频分复用

OFDM（OrthogonalFrequencyDivisionMultiplexing）实际是一种多载波数字调制技术。

OFDM全部载波频率有相等的频率间隔，它们是一个基本振荡频率的整数倍，正交指各个载波的信号频谱是正交的。

OFDM系统比FDMA系统要求的带宽要小得多。

由于OFDM使用无干扰正交载波技术，单个载波间无需保护频带，这样使得可用频谱的使用效率更高。

另外，OFDM技术可动态分配在子信道中的数据，为获得最大的数据吞吐量，多载波调制器可以智能地分配更多的数据到噪声小的子信道上。

目前OFDM技术已被广泛应用于广播式的音频和视频领域以及民用通信系统中，主要的应用包括：

非对称的数字用户环线（ADSL）、数字视频广播（DVB）、高清晰度电视（HDTV）、无线局域网（WLAN）和第4代（4G）移动通信系统等。

频分复用系统最大的优点是信道复用率高，允许的复用路数较多，同时分路也很方便，是模拟通信中主要的一种复用方式，在有线和微波通信中应用十分广泛。

频分复用的缺点是设备生产较为复杂，同时因滤波性能不够理想，及信道内存在的非线性容易产生路间干扰。

2、F