最新弹性力学答案清晰修改.docx
《最新弹性力学答案清晰修改.docx》由会员分享,可在线阅读,更多相关《最新弹性力学答案清晰修改.docx(22页珍藏版)》请在冰豆网上搜索。
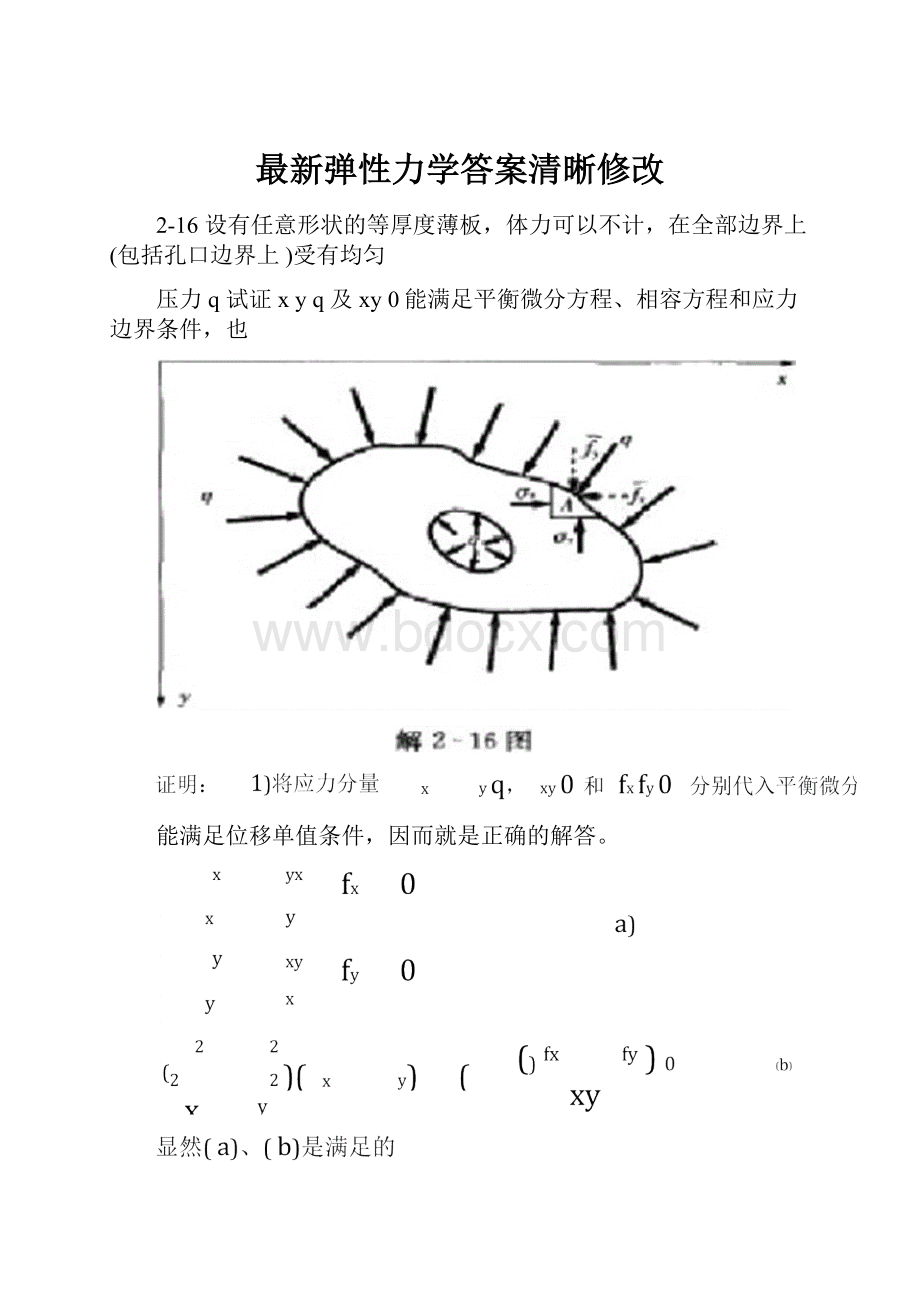
最新弹性力学答案清晰修改
2-16设有任意形状的等厚度薄板,体力可以不计,在全部边界上(包括孔口边界上)受有均匀
压力q试证xyq及xy0能满足平衡微分方程、相容方程和应力边界条件,也
能满足位移单值条件,因而就是正确的解答。
程、相容方程
2)对于微小的三角板A,dx,dy都为正值,斜边上的方向余弦lcos(n,x),mcos(n,y),
将xyq,xy0代入平面问题的应力边界条件的表达式
(lxmyx)sfx(s)
(c)
(mylxy)sfy(s)
则有xcos(n,x)qcos(n,x)ycos(n,y)qcos(n,y)
所以xq,yq。
对于单连体,上述条件就是确定应力的全部条件。
(3)对于多连体,应校核位移单值条件是否满足。
该题为平面应力的情况,首先,将应力分量xyq及xy0代入物理方程,得形
变分量x(E1)q,y(E1)q,xy0(d)
然后,将(d)的变形分量代入几何方程,得
其中的f1和f2分别是y和x的待定函数,可以通过几何方程的第三式求出,将式(f)代
入(e)的第三式得df1(y)df2(x)
dydx
等式左边只是y的函数,而等式右边只是x的函数。
因此,只可能两边都等于同一个常数ω,
代入(f)得位移分量
其中u0,v0,为表示刚体位移量的常数,须由约束条件求得。
从式(g)可见,位移是坐标的单值连续函数,满足位移单值条件,因而,应力分量是正确的解答。
0,然后证明,这些表达
2-17设有矩形截面的悬臂粱,在自由端受有集中荷载F,体力可以不计。
试根据材料力学
公式,写出弯应力x和切应力xy的表达式,并取挤压应力
解〔1〕矩形悬臂梁发生弯曲变形,任意横截面上的弯矩方程为M(x)Fx,横
截面对z
轴(中性轴)的惯性矩为I
h3
根据材料力学公式,
弯应力
xy
M(x)y
Iz
123Fxy;该截面上的剪力为Fs(x)Fh
剪应力
3Fs(x)(I
2h(I
4hy22)
6F3(hy2);并取挤压应力y0
h4
2)经验证,上述表达式能满足平衡微分方程
yx
xy
2
也能满足相容方程(
2)(xy)(1()
y2x
再考察边界条件:
在
h/2的主要边界上,应精确满足应力边界条件:
y)yh/2
0,
(yx)yh/20;
y)yh/2
0,
(yx)yh/20。
在次要边界
能满足
x=0上,列出三个积分的应力边界条件:
h/2
h/2
h/2
x)x0dy
h/2
h/2
x)x0ydy
h/2
xy)x0dy
h/2
h/2
12F
h/2
(
x)x
ldy
h/2
3lydy0h3
h/2
h/2
12F2
h/2
(
x)x
lydy
h/2
3ly2Flh3
h/2
h/2
6Fh22
h/2
(
xy)x
0dy
h/2
h3(4y2)
h4
列出三个积分的应力边界条件:
满足应力边界条件。
在次要边界xl上,
满足应力边界条件因此,他们是该问题的解答。
3-6如题3-6图所示的墙,高度为
h,宽度为b,
h?
b,在两侧面上受到均布剪力
q的作用。
试用应力函数
AxyBx2y求解应力分量。
4
解
(1)相容条件:
将应力函数
4
4
4
4
0,40,
2
20
很明显满足相容方程。
x
y
xy
2)
应力分量表达式
2
2
2
x
20,y
2
6Bxy,
xyA3Bx2
y2
x
xy
3)
考察边界条件:
在主
要边界
x
b/2上,各有两个应精确满足的边界条件,即
x)
xb/20,(xy)x
b/2
q。
代人相容方程
0中,其中
0的条件不可能精确满足(否则只有
而
在次要边界y0上,(y)y
(yx)y0
00
A=B=0),可用积分的应力边界条件代替
b/2
b/2(
yx)y0dx0
4)把各应力分量代入边界条件,得
Aq2
,B2bq2。
b
应力分量为
0,y1b22qxy,
b
x2
xy
q
q2(112b2)
3-8设题3-8图中的三角形悬臂梁只受重力作用,而梁的密度为函数求解。
,试用纯三次式的应力
解
(1)相容条件:
3223
设AxBxyCxyDy(a)
不论上述中的系数取何值,纯三次式的应力函数总能满足相容方程。
3)考察边界条件:
利用边界条件确定待定系数
先考察主要边界上y0的边界条件:
(y)y00,(yx)y00
将应力分量式(b)和式(c)代入,这些边界条件要求
e)
(y)y06Ax0,(xy)y02Bx0得A=0,B=0。
式(b)、(c)、(d)成为
ygy
(f)
xy2Cy
(g)
根据斜边界的边界条件
它的边界线方程是
yxtan,在斜面上没有任何面力,即
x
2Cx6Dy
fxfy0,按照一般的应力边界条件,有
由应力函数得应力分量
22
2(Acos2Bsin2CD)
(1)2Asin22Bcos2C
2)考察边界条件:
根据对称性,得
(
)/2
0
(a)
(
)/2
q
(b)
(
)/2
0
(c)
(
)/2
q
(d)
由式(
a)
得2Acos
2Bsin
C
2D
0
(e)
由式(
b)
得2Asin
2Bcos
C
q
(f)
由式(
c)
得2Acos
2Bsin
C
2D
0
(g)
由式(
d)
得
2Asin
2Bcos
C
q
(h)
式(e)、(f)、(g)、(h)联立求解,得Aq,BC0,Dqcot
2sin2
将以上系数代入应力分量,得
cos2
q(cos2cot)
sin
cos2
q(cos2cot)
sin
sin2
qsin
4一13设有内半径为r,外半径为R的圆筒受内压力q,试求内半径和外半径的改变,并求圆筒厚度的改变。
解本题为轴对称问题,只有径向位移而无环向位移。
当圆筒只受内压力q的情况下,取应力分量表达式(B=0),内外的应力边界条件要求
(
)r0,(
)R0
(
)rq,(
)R0
由表达式可见,
前两个关于
的条件是满足的,而后两个条件要求
A
2r
A
R2
把A,B,C值代入轴对称应力状态下对应的位移分量,
2
E(Rq2r2r2)
(1)
(1
R2
)IcosKsin
b)
HIsinKcos
(c)
式(c)中的,取任何值等式都成立,所以个自由项的系数为零所以,轴对称问题的径向位移式(b)为
H=I=K=0。
22qrRu22
(1)
(1)E(R2r2)
而圆简是属于平面应变问题,故上式中E
E,
12,
代替,则有
u
uq(11
22
)R2
(1)2
1
E2(Rr21)
r
此时内径改变为
ur
2
(1)R2(1
1q2q1Er2(Rr221)
1r
1)r2
qr(1
E
22
2)(RR22
),
外径改变为uR
(1
q
22
)R2
(1)R2
11
2
ER2(Rr221)
r
圆环厚度的改变为
uRur
qr(12)(Rr
E(Rr
qr(1
E
1)
4-15在薄板内距边界较远的某一点处,应.力分最为x
一小圆孔.试求孔边的最大正应力。
2
2)2Rr
22
Rr
0,
xyq,如该处有
解求出两个主应力,即
1
2
原来的间题变为矩形薄板在左右两边受均布拉力q而在上下两边受均布压力q,如图所示。
应力分量x
q,
yq,
xy
0代入坐标变换式,得到外边界上的边界条件
(
)R
qcos2
(a)
(
)R
qsin2
(b)
在孔边,边界条件是
(
)r
0(
c)
(
)r
0
(d)
由边界条件式(a)、(b)、(c)、(d)可见,用办逆解法是,可假设为的某一函数乘以
(1
删去因子cos2以后,求解这个常微分方程,得
由应力函数得应力分量的表达式
将上式代入应力边界条件
得2B
R2
R4
q
(g)
2
2C
6D
得6AR
2B
2
4q
(h)
R2
R4
4C
6D
得2B
2
4
0
(i)
r
r
2
2C
6D
得6Ar2
2B
2
6D40
(j)
由式(a)
由式(b)
由式(c)
由式(d)
r
r
将各系数值代入应力分量的去达式,
沿着孔边r,环向正应力是4qcos2
最大环向正应力为()max4q
4-17在距表面为h的弹性地基中,挖一直径为d的水平圆形孔道,设h》d,弹性地基的密度为,弹性模量为E,泊松比为,试求小圆孔附近的最大、最小应力。
2)原来的问题变为管道在左右两边受均布压力在上下两边受均布压力gh,在上下
1
两边受均布压力gh,如图(a)所示。
可以将荷载分解为两部分:
第一部分是四边的均
布压力12gh如图(b)所示,第二部分是左右两边的均布拉力22
(1)
12(12)gh和上下两边的均布压力12(12)gh如图(c)所示。
22
(1)22
(1)
2r对于第一部分荷载,可应用解答q(12)
R2
对于第二部分解答,可应用解答,教材中式(4-18)。
将两部分解答叠加,即得原荷载作用
下的应力分量(基尔斯的解答)。
解按应力求解空间问题时,须要使得六个应力分量在弹性体区域内满足平衡徽分方程,满足相容方程;并在边界上满足应力边界条件.
(l)fxfy0,fzg很显然应力分量满足如下平衡徽分方程
x
yx
zx
fx
0
x
y
z
y
zy
xy
fy
0
y
z
x
z
xz
yz
fz
0
z
x
y
2)
xyx
z
gz,
应力分量也满足贝尔特拉米相容方程
2
)2
2
(1
)2
x2
0
(1
xy
0
x
x
y
2
)2
2
(1
)2
y2
0
(1
yz
0
y
y
z
2
)2
2
(1
)2
z2
0
(1
xz
0
z
x
z
3)考察应力边界条件:
柱体的侧面和下端面,
fx
fy
fz
0。
.在(x,y)平面上应考
虑为任意形状的边界(侧面方向余弦分别为
n0,l,m为任意的;在下端面方向余弦分别为
n1,lm0)。
应用一般的应力边界条件,将应力和面力分量、方向余弦分别代入下
(lxmyxnzx)s(mynzylxy)s(nxlxzmyz)s
直杆的侧面和下端的应力边界条件都能满足,因此,所给应力分是是本问题的解
8-2设有任意形状的空间弹性体,在全部边界上(包括在孔洞边界上)受有均布压力q,试证应力分量xyzq,yzzxxy0能满足一切条件,因而就是正确的解答。
解:
应力应满足平衡微分方程,相容方程及应力边界条件(在s上),多连体还应满足位移单值条件。
(1)
(2)平衡条件fxfyfz0,很显然,应力分量满足平衡微分方程
3)
4)相容条件:
xyz3q,应力分量也满足贝尔特拉米相容方程。
(3)应力边界条件。
考虑一般的应力边界条件:
法线的方向余弦为l,m,n边界面为任意斜
面,受到法向压力q的作用。
同样,满足应力的边界条件。
(4)位移单值条件,为了考虑多连体中的位移单值条件,由应力求出对应的位移,然后再检查是否满足单值条件。
将应力分量代人教材中式(7一12),得形变分量表达式
21
将形变分量代入几何方程,得
其中的f1,f2,f3分别是y,z和x,z和x,y的待定函数,可以通过几何方程的后三个式子求出。
u0
v0
2f3
代入位移分量表达式得
其中u0,v0,
分量分别表示位移和刚体转动,与形变无关。
多连体上各
个点的位移分量都是x,y,z的线性函数,所以满足位移单值条件。