北师大版七年级下册数学期末复习几何压轴题训练.docx

北师大版七年级下册数学期末复习几何压轴题训练.docx

《北师大版七年级下册数学期末复习几何压轴题训练.docx》由会员分享，可在线阅读，更多相关《北师大版七年级下册数学期末复习几何压轴题训练.docx（15页珍藏版）》请在冰豆网上搜索。

北师大版七年级下册数学期末复习几何压轴题训练

2019年北师大版七年级下册期末复习：

几何压轴题训练

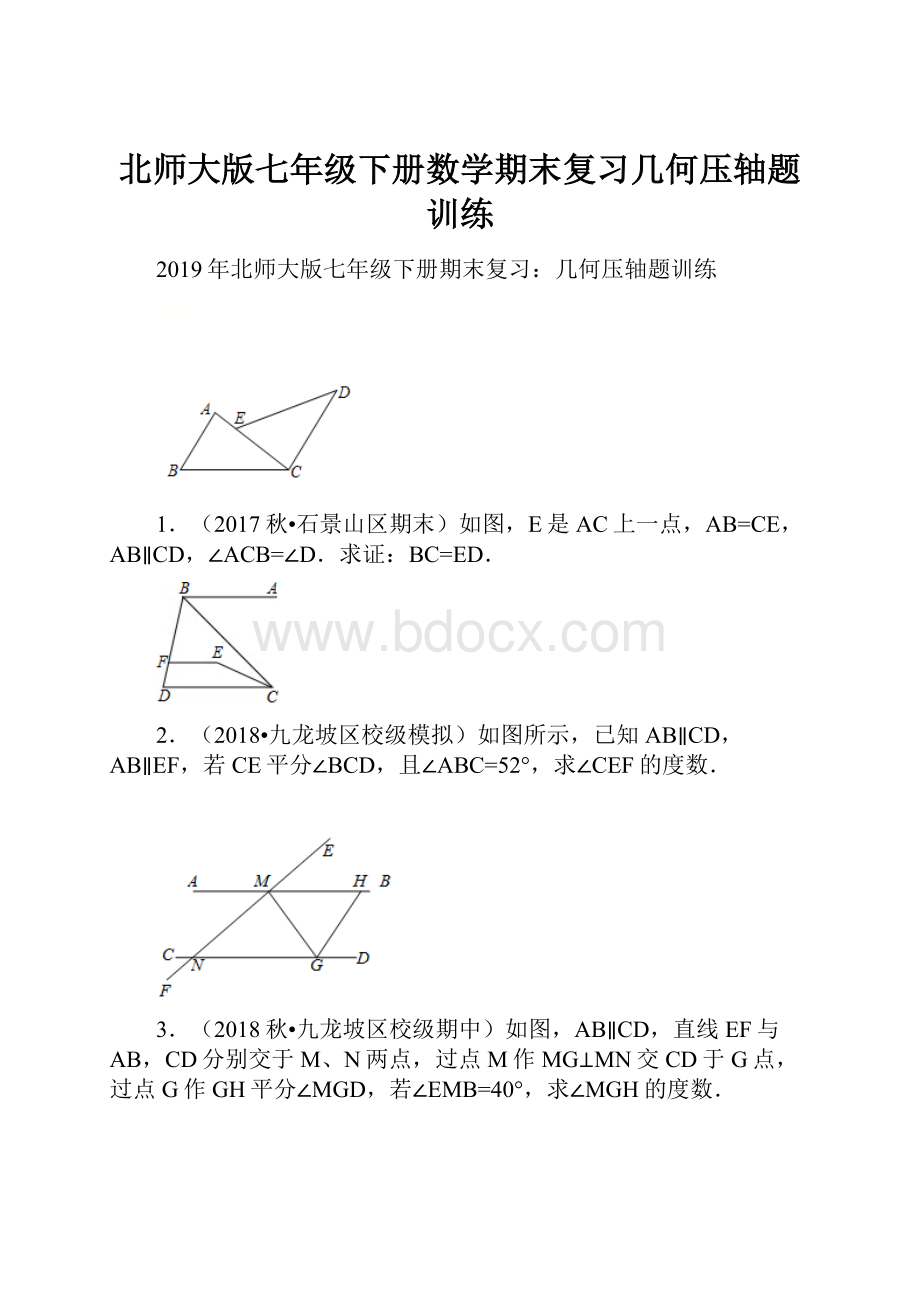
1．（2017秋•石景山区期末）如图，E是AC上一点，AB=CE，AB∥CD，∠ACB=∠D．求证：

BC=ED．

2．（2018•九龙坡区校级模拟）如图所示，已知AB∥CD，AB∥EF，若CE平分∠BCD，且∠ABC=52°，求∠CEF的度数．

3．（2018秋•九龙坡区校级期中）如图，AB∥CD，直线EF与AB，CD分别交于M、N两点，过点M作MG⊥MN交CD于G点，过点G作GH平分∠MGD，若∠EMB=40°，求∠MGH的度数．

4．（2018秋•沙坪坝区校级期中）如图，AB∥CD，点E在线段AB上，连接EC、ED、AD，且ED平分∠CEB，AD⊥EF，若∠ADC=42°，∠A-∠B=8°，求∠BDE的度数．

5．（2018春•庐阳区期末）如图1，点E在直线AB上，点F在直线CD上，EG⊥FG．

（1）若∠BEG+∠DFG=90°，请判断AB与CD的位置关系，并说明理由；

（2）如图2，在

（1）的结论下，当EG⊥FG保持不变，EG上有一点M，使∠MFG=2∠DFG，则∠BEG与∠MFD存在怎样的数量关系？

并说明理由．

（3）如图2，若移动点M，使∠MFG=n∠DFG，请直接写出∠BEG与∠MFD的数量关系．

6．（2017秋•确山县期末）如图所示，∠B=25°，∠D=42°，∠BCD=67°，试判断AB和ED的位置关系，并说明理由．

7．（2018春•泰山区期中）如图，DE平分∠ADC，CE平分∠BCD，且∠1+∠2=90°．试判断AD与BC的位置关系，并说明理由．

8．（2018秋•上杭县期中）如图，点D在△ABC的边AB上，且∠ACD=∠A．

（1）作∠BDC的平分线DE，交BC于点E．（要求：

尺规作图，保留作图痕迹，但不必写出作法）；

（2）在

（1）的条件下，求证：

DE∥AC．

9．（2018春•相城区期中）将一副直角三角尺BAC和ADE如图放置，其中∠BAC=∠ADE=90°，∠BCA=30°，∠AED=45°，若∠AFD=75°，试判断AE与BC的位置关系，并说明理由．

10．（2018春•容县期中）如图，直线AB，CD相交于点O，OA平分∠EOC．已知∠DOE=2∠AOC，求证：

OE⊥CD．

11．（2018春•鱼台县期中）课题学习：

平行线的“等角转化”功能．

阅读理解：

如图1，已知点A是BC外一点，连接AB，AC．

求∠BAC+∠B+∠C的度数．

（1）阅读并补充下面推理过程

解：

过点A作ED∥BC，所以∠B=∠EAB，∠C=．

又因为∠EAB+∠BAC+∠DAC=180°，

所以∠B+∠BAC+∠C=180°

解题反思：

从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决．

方法运用：

（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．（提示：

过点C作CF∥AB）

深化拓展：

（3）如图3，已知AB∥CD，点C在点D的右侧，∠ADC=70°．点B在点A的左侧，∠ABC=60°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间，求∠BED的度数．

12．（2018秋•连城县期中）已知：

如图所示，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A+∠1=70°，求：

∠D的度数．

13．（2017秋•固始县期末）如图，把一张长方形纸片沿EF折叠后，点D，C分别落在点D′，C′的位置，若∠DEF=75°，则∠AED′等于多少？

14．（2018秋•沙坪坝区校级月考）如图，MN∥PQ，点A在MN上，点B在PQ上，连接AB，过点A作AC⊥AB交PQ于点C．过点B作BD平分∠ABC交AC于点D，若∠NAC=32°，求∠ADB的度数．

15．（2017秋•洛宁县期末）观察，在如图所示的各图中找对顶角（不含平角）：

（1）如图a，图中共有对对顶角．

（2）如图b，图中共有对对顶角．

（3）如图c，图中共有对对顶角

（4）研究

（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成多少对对顶角？

（5）若有2000条直线相交于一点，则可形成多少对对顶角？

16．（2017秋•孟津县期末）如图，AB、CD相交于点O，OE是∠AOD的平分找，∠AOC=25°，求∠BOE的度数．

17．（2018春•长白县期中）如图所示，已知直线DE∥BC，GF⊥AB于点F，∠1=∠2，判断CD与AB的位置关系．并说明理由．

18．（2017秋•永安市期末）直线AB、CD被直线EF所截，AB∥CD，点P是平面内一动点．设∠PFD=∠1，∠PEB=∠2，∠FPE=∠α．

（1）若点P在直线CD上，如图①，∠α=50°，则∠1+∠2=°；

（2）若点P在直线AB、CD之间，如图②，试猜想∠α、∠1、∠2之间的等量关系并给出证明；

（3）若点P在直线CD的下方，如图③，

（2）中∠α、∠1、∠2之间的关系还成立吗？

请作出判断并说明理由．

19．（2017秋•辉县市期末）如图，直线AB∥CD，直线EF与AB相交于点P，与CD相交于点Q，且PM⊥EF，若∠1=68°，求∠2的度数．

20．（2018春•罗庄区期中）如图，已知AB∥CD，EF∥MN，∠1=115°．

（1）求∠2和∠4的度数；

（2）本题隐含着一个规律，请你根据

（1）的结果进行归纳，试着用文字表述出来．

（3）利用

（2）的结论解答：

如果两个角的两边分别平行，其中一角是另一个角的2倍多6°，求这两个角的大小．

21．（2017秋•洛宁县期末）如图，直线AB∥CD，EF⊥CD，F为垂足，∠GEF=30°，求∠1的度数．

22．（2018春•奉贤区期中）如图，已知，∠3=∠B，∠1+∠2=180°，∠AED=∠C大小相等吗？

请说明理由．

请完成填空并补充完整．

解：

因为∠1+∠2=180°（已知）

又因为∠2+∠=180°（邻补角的意义）

所以∠1=∠（）#JB

23．（2018春•兰陵县期中）

（1）探究：

如图1，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=40°，求∠DEF的度数．

（2）应用：

如图2，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=60°，求∠DEF的度数．

24．（2018秋•綦江区校级月考）如图：

已知EF∥AD，∠1=∠2，∠AGD=108°．求∠BAC的度数．

25．（2017秋•渝中区校级期末）如图1，已知A、O、B三点在同一直线上，射线OD、OE分别平分∠AOC、∠BOC．

（1）求∠DOE的度数；

（2）如图2，在∠AOD内引一条射线OF⊥OC，其他不变，设∠DOF=ao（oo＜a＜90o）．

a．求∠AOF的度数（用含a的代数式表示）；

b．若∠BOD是∠AOF的2倍，求∠DOF的度数．

26．（2018•九龙坡区校级模拟）如图，AB∥CD，点E在AB上，点F在CD上，连接EF，EH平分∠BEF，交CD于点H，过F作FG⊥EF，交EH于点G，若∠G=32°，求∠HFG的度数．

27．（2018春•大田县期中）如图，如果∠1=∠2，那么图中哪两条线段平行？

请说明理由．

28．（2018春•大田县期中）如图，AB∥CD，直线EF交AB于点G，交CD于点H，HM⊥CD于点H，如果∠1=48°，求∠2的度数．

29．（2018春•杏花岭区校级期中）如图，已知AM∥BN，∠A=60°，点P是射线M上一动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

（1）∠CBD=

（2）当点P运动到某处时，∠ACB=∠ABD，则此时∠ABC=

（3）在点P运动的过程中，∠APB与∠ADB的比值是否随之变化？

若不变，请求出这个比值：

若变化，请找出变化规律．

30．（2018秋•宁阳县期中）已知：

如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2．求证：

EF∥CD．

31．（2017秋•南召县期末）阅读理解

如图1，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数．

（1）阅读并补充下面推理过程

解：

过点A作ED∥BC

∴∠B=∠，∠C=∠．

又∵∠EAB+∠BAC+∠DAC=180°（平角定义）

∴∠B+∠BAC+∠C=180°

从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决

（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．

小明受到启发，过点C作CF∥AB如图所示，请你帮助小明完成解答：

（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°．BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．

①如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为°．

②如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为°（用含n的代数式表示）

32．（2018春•西城区校级期中）如图，∠1=∠2，AB∥EF，求证：

∠3=∠4．

33．（2017秋•惠阳区期末）如图，直线EF∥GH，点A在EF上，AC交GH于点B，若∠EAB=110°，∠C=60°，点D在GH上，求∠BDC的度数．

34．（2017秋•南召县期末）操作：

如图，直线AB与CD交于点O，按要求完成下列问题．

（1）用量角器量得∠AOC=度．AB与CD的关系可记作．

（2）画出∠BOC的角平分线OM，∠BOM=∠=度．

（3）在射线OM上取一点P，画出点P到直线AB的距离PE．

（4）如图若按“上北下南左西右东”的方位标记，请画出表示“南偏西30°”的射线OF．

35．（2018春•北海期末）如图，直线AB，CD，EF相交于点O，∠AOE：

∠AOD=1：

3，∠COB：

∠DOF=3：

4，求∠DOE的度数．

36．（2017秋•淅川县期末）观察发现：

已知AB∥CD，点P是平面上一个动点．当点P在直线AB、CD的异侧，且在BC（不与点B、C重合）上时，如图

（1），容易发现：

∠ABP+∠DCP=∠BPC．

拓展探究：

（1）当点P位于直线AB、CD的异侧，且在BC左侧时，如图

（2），∠ABP、∠DCP、∠BPC之间有何关系？

并说明理由．

（2）当点P位于直线AB、CD的异侧，且在BC右侧时，如图（3），直接写出∠ABP、∠DCP、∠BPC之间关系．

（3）当点P位于直线AB、CD的同侧，如图（4），直接写出∠ABP、∠DCP、∠BPC之间关系．

37．（2018春•上饶县期末）

（1）如图1，AM∥CN，求证：

①∠MAB+∠ABC+∠BCN=360°；

②∠MAE+∠AEF+∠EFC+∠FCN=540°；

（2）如图2，若平行线AM与CN间有n个点，根据

（1）中的结论写出你的猜想并证明．

38．（2017秋•金牛区校级期末）如图，已知AB∥CD，若∠C=35°，AB是∠FAD的平分线．

（1）求∠FAD的度数；

（2）若∠ADB=110°，求∠BDE的度数．

39．（2017秋•新野县期末）

（1）如图1，已知AB∥CD，求证：

∠BED=∠1+∠2．

（2）如图2，已知AB∥CD，写出∠1、∠EGH与∠2、∠BEG之间数量关系，并加以证明．

（3）如图3，已知AB∥CD，直接写出∠1、∠3、∠5、与∠2、∠4、∠6之间的关系．

40．（2018春•上饶县期末）如图，已知∠1=∠2，AB∥EF．求证：

∠A=∠E．