中考数学复习冲刺几何提升第6讲弦图模型.docx

中考数学复习冲刺几何提升第6讲弦图模型.docx

《中考数学复习冲刺几何提升第6讲弦图模型.docx》由会员分享，可在线阅读，更多相关《中考数学复习冲刺几何提升第6讲弦图模型.docx（19页珍藏版）》请在冰豆网上搜索。

中考数学复习冲刺几何提升第6讲弦图模型

中考数学几何模型6：

弦图模型

拨开云雾开门见山

名师点睛

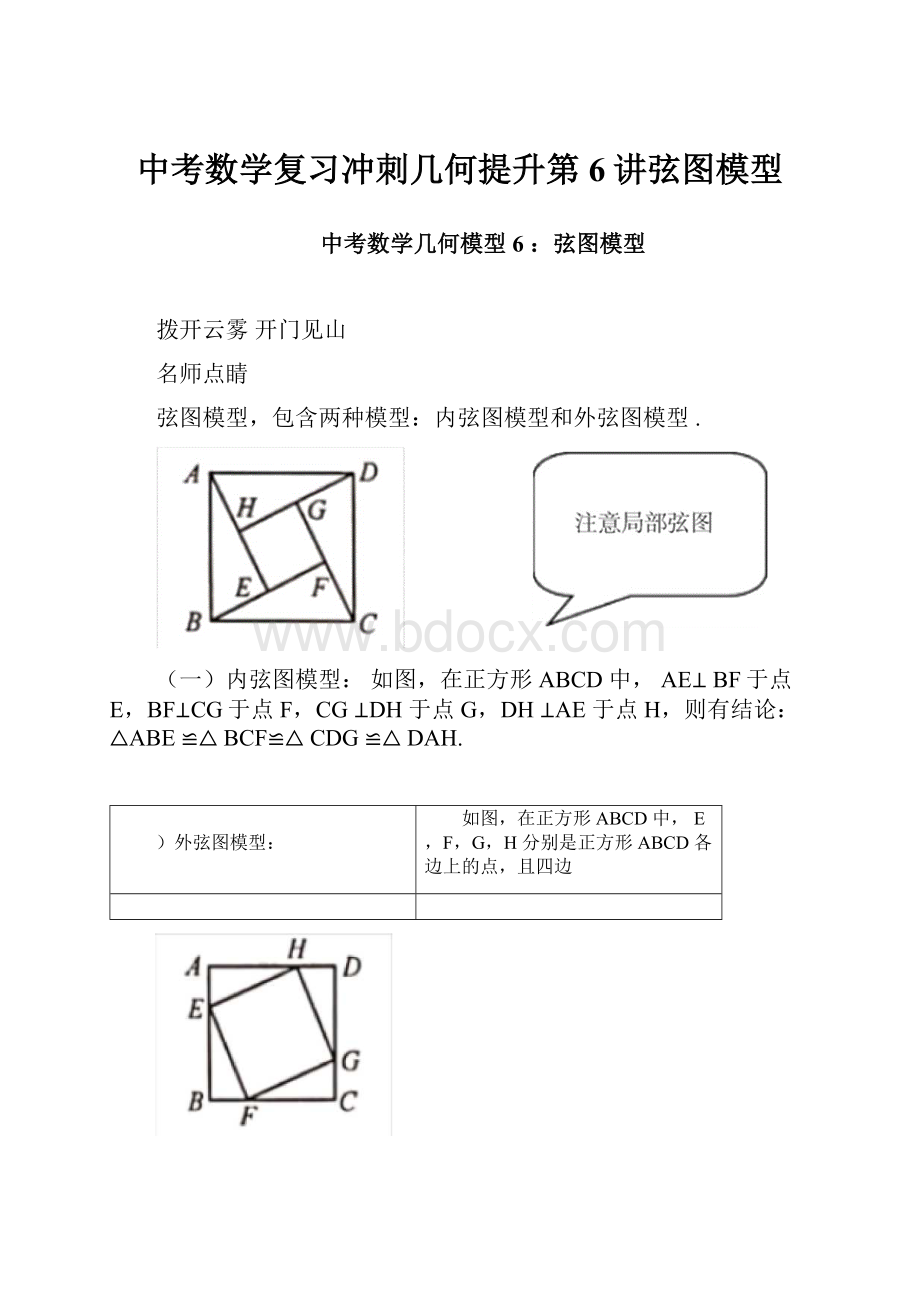
弦图模型，包含两种模型：

内弦图模型和外弦图模型.

（一）内弦图模型：

如图，在正方形ABCD中，AE⊥BF于点E，BF⊥CG于点F，CG⊥DH于点G，DH⊥AE于点H，则有结论：

△ABE≌△BCF≌△CDG≌△DAH.

）外弦图模型：

如图，在正方形ABCD中，E，F，G，H分别是正方形ABCD各边上的点，且四边

形EFGH是正方形，则有结论：

△AHE≌△BEF≌△CFG≌△DGH.

启迪思维探究重点

典题探究

例题1.如图，在△ABC中，∠ABC=90°，分别以AB，AC向外作正方形ABDE，ACFG，连接EG，若AB=12，BC=16，求△AEG的面积.

例题2.如图，以Rt△ABC的斜边BC在△ABC同侧作正方形BCEF，该正方形的中心为点O，连接AO.

若AB=4，AO=62，求AC的长.

变式练习>>>

2．如图，点A，B，C，D，E都在同一条直线上，四边形X，Y，Z都是正方形，若该图形总面积是m，

例题3.如图，在△ABC中，∠BAC=45°，D为△ABC外一点，满足∠CBD=90°，BC=BD，若S△ACD=4.5，

求AC的长.

变式练习>>>

3．点P是正方形ABCD外一点，ABCD的面积.

PB=10cm，△APB的面积是60cm2，△CPB的面积是30cm2．求正方形

例题4.在边长为10的正方形ABCD中，内接有6个大小相同的正方形，边上的小正方形的顶点，如图所示，求这六个小正方形的面积.

P、Q、M、N是落在大正方形

变式练习>>>

4．如图，在平面直角坐标系中，经过点A的双曲线y＝（x>0）同时经过点B，且点A在点B的左侧，

1+．

∴△AOM≌△BAN（AAS），∴AM＝BN＝，OM＝AN＝

，∴OD＝

+，BD

+，

+

解得：

k＝1±

∴k＝1+；

∴B（

∴（

），∴双曲线y

x>0）同时经过点A和

﹣）＝k，整理得：

k2﹣2k﹣4＝0，

（负值舍去），

故答案为：

1+例题上，

（1）

（2）

5.

若

若

如图，在等腰Rt△ACB和等腰

IC⊥BE，求证：

I为AD中点；I为AD中点，求证：

IC⊥BE

B，

Rt△DCE中，∠AXB=∠DCE=90°

，连接AD，BE，点I在AD

达标检测

所有点P的坐标，如不存在，请说明理由

领悟提升强化落实

1.如图所示，“赵爽弦图”是由8个全等的直角三角形拼接而成的

l移动的过程中，直线y=4上是否存在点P，使得△PAB是等腰直角三角形，若存在，请求出满足条件的

例题6.在平面直角坐标系中，直线l的解析式为y2xb，其与x轴交于点A,与y轴交于点B，在直线

正方形MNKT的面积分别为S1，S2，S3，已知S1+S2+S3＝10，则S2的值是

记图中正方形ABCD，正方形EFGH．

解答】解：

将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，

∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3＝10，∴得出S1＝8y+x，S2＝4y+x，S3＝x，

∴S1+S2+S3＝3x+12y＝10，故3x+12y＝10，

x+4y＝，所以S2＝x+4y＝，

故答案为53．如图，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，

BG，EG．（正方形的各边都相等，各角均为90°）

（1）判断CE与BG的关系，并说明理由；

（2）若BC＝3，AB＝5，则AEG面积等于6．

解答】解：

（1）如图，

∵∠EAB＝∠GAC＝90°，∴∠EAC＝∠BAG，

在△EAC和△BAG中，，

∴△EAC≌△BAG（SAS），

∴CE＝BG，∠AEC＝ABG，

∵∠AEC+∠APE＝90°，∠APE＝∠BPC，

∴∠BPC+∠ABG＝90°，

∴CE⊥BG；

（2）延长GA，过E作EQ⊥AQ，

∵∠EAB＝∠GAC＝90°，

∴∠EAG+∠BAC＝180°，

∵∠EAG+∠EAQ＝180°，

∴∠EAQ＝∠BAC，

∴EQ＝AE?

sin∠EAQ＝AB?

BC＝3，

∵BC＝3，AB＝5，

∴AC＝＝4，

∴AEG面积＝

4．【问题解决】

一节数学课上，老师提出了这样一个问题：

如图1，

＝3．你能求出∠APB的度数吗？

小明通过观察、分析、思考，形成了如下思路：

思路一：

将△BPC绕点B逆时针旋转90°，得到△思路二：

将△APB绕点B顺时针旋转90°，得到△请参考小明的思路，任选一种写出完整的解答过程．

点P是正方形ABCD内一点，PA＝1，PB＝2，PC

BP′A，连接PP′，求出∠APB的度数；CP'B，连接PP′，求出∠APB的度数．

类比探究】

如图2，若点P是正方形ABCD外一点，PA＝3，

PB＝1，PC＝，求∠APB的度数．

解答】解：

（1）思路一、如图1，

将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′∴△ABP'≌△CBP，

∴∠PBP'＝90°，BP'＝BP＝2，AP'＝CP＝3，

在Rt△PBP'中，BP＝BP'＝2，

∴∠BPP'＝45°，根据勾股定理得，PP'＝BP＝2，

∵AP＝1，

∴AP2+PP'2＝1+8＝9，

∵AP'2＝32＝9，

∴AP2+PP'2＝AP'2，

∴△APP'是直角三角形，且∠APP'＝90°，

∴∠APB＝∠APP'+∠BPP'＝90°+45°＝135°；

（2）如图2，

将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′

∴△ABP'≌△CBP，

∴∠PBP'＝90°，BP'＝BP＝1，AP'＝CP＝，

在Rt△PBP'中，BP＝BP'＝1，

∴∠BPP'＝45°，根据勾股定理得，PP'＝BP＝，

∵AP＝3，

∴AP2+PP'2＝9+2＝11，

∵AP'2＝（）2＝11，

∴AP2+PP'2＝AP'2，

∴△APP'是直角三角形，且∠APP'＝90°，

∴∠APB＝∠APP'﹣∠BPP'＝90°﹣45°＝45°．

5．如图，已知∠ABC＝90°，D是直线AB上一点，AD＝BC．

（1）如图1，过点A作AF⊥AB，并截取AF＝BD，连接DC、DF、CF．

①求证：

AF+AB＝BC

②判断FD与DC的关系并证明；

（2）如图2，E是直线BC上一点，且CE＝BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？

若是，请求出它的度数；若不是，请说明理由．

【解答】

（1）证明：

①∵AD＝BC，∴AD＝AB+BD，AF＝BD，∴AF+AB＝BC．

②∵AF⊥AB，∴∠FAD＝90°，又∵∠DBC＝90°，∴∠FAD＝∠DBC，∵AF＝BD，AD＝BC，∴△FAD≌△DBC（SAS），

∴FD＝CD，∠ADF＝∠BCD，∴∠BDC+∠ADF＝∠BDC+∠BCD＝90°，即DF⊥DC；

（2）解：

作AF⊥AB于A，使AF＝BD，连结DF，CF，如图，∵AF⊥AD，∠ABC＝90°，∴∠FAD＝∠DBC，

在△FAD与△DBC中，，∴△FAD≌△DBC（SAS），

∴FD＝DC，∴△CDF是等腰三角形，

∵△FAD≌△DBC，∴∠FDA＝∠DCB，

∵∠BDC+∠DCB＝90°，∴∠BDC+∠FDA＝90°，

∴△CDF是等腰直角三角形，∴∠FCD＝45°，

∵AF∥CE，且AF＝CE，∴四边形AFCE是平行四边形，

∴AE∥CF，∴∠APD＝∠FCD＝45°．

6．【探究证明】

（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．

如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H，求

证：

；

【结论应用】

（2）如图2，在满足

（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若，

则的值为；（直接写出结果）

【联系拓展】（3）如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝6，BC＝CD＝3，AM⊥DN，点M，N分别在边BC，AB上，求的值．

∵AM⊥DN，

∴由

（1）中的结论可得．

设SC＝x，DS＝y，则AR＝BS＝3+x，RD＝6﹣y，∴在Rt△CSD中，x2+y2＝9①，

在Rt△ARD中，（3+x）2+（6﹣y）2＝36②，由②﹣①得x＝2y﹣3③，

8．提出问题：

如图1，在△ABC中，∠ACB＝90°，分别以边AB、AC向外作正方形ABDE和正方形ACFG，连接CE，BG，EG．

（1）探索CE与BG的关系；

（2）探究△ABC与△AEG面积是否仍然相等？

说明理由．

（3）如图2，学校教学楼前的一个六边形花圃被分成七个部分，分别种上不同品种的花卉，已知△CDG

是直角三角形，∠CGD＝90°，DG＝3m，CG＝4m，四边形ABCD、CIHG、GFED均为正方形，则这

个六边形花圃ABIHFE的面积为

理由：

∵∠EAB＝∠GAC＝90°，∴∠EAC＝∠BAG，

在△EAC和△BAG中，，∴△EAC≌△BAG（SAS），

∴CE＝BG，∠AEC＝ABG，

∵∠AEC+∠APE＝90°，∠APE＝∠BPC，∴∠BPC+∠ABG＝90°，

∴CE⊥BG；即：

CE＝BG，CE⊥BG；

（2）如图1，

过点E作EH⊥AG交GA延长线于H；∴∠EHA＝∠90°＝∠BCA，

∵∠EAH+∠BAH＝90°，∠BAC+∠BAH＝90°，

∴∠EAH＝∠BAC，

在△EHA和△BCA中，，

∴△EHA≌△BCA，∴EH＝BC，

∵AC＝AG∴S△ABC＝AC×BC＝AC×EH，ABC

S△AGE＝AG×EH＝AC×EH，AGE

∴S△ABC＝S△AGE，

（3）∵在Rt△CDG中，DG＝3m，CG＝4m，∴CD＝5m，

∵四边形ABCD，CIHG、GFED均为正方形

∴CG＝GH＝4，DG＝FG＝3，

同

（2）的方法得出S△BCI＝S△CDG，S△ADE＝S△CDG

∴S六边形花圃ABIHFE＝S正方形ABCD+S△BCI+S正方形CIHG+S△FGH+S正方形DEFG+S△ADE+S△SDG＝S正方形ABCD+S△CDG+S正方形CIHG+S△FGH+S正方形DEFG+S△CDG+S△CDG

＝S正方形ABCD+S正方形CIHG+S△FGH+S正方形DEFG+3S△CDG

＝CD2+CG2+

＝52+42+

×4×3+32+×4×3

＝25+16+6+9+18

＝74（m2）．故答案为74m2．

9．已知：

l1∥l2∥l3∥l4，平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3，且d1＝d3＝1，d2l2、l3、l4这四条平行线上的四边形称为“格线四边形”．

1）如图

1，正方形ABCD为“格线四边形”，

则正方形ABCD的边长为

（2）矩形

（3）如图A顺时针旋转30°得到∠AE′D′（如图

AB′C′D′，使B′，C′分别在直线l2，l4上，求菱形AB′C′D′的边长．【解答】解：

（1）∵l1∥l2∥l3∥l4，∠AED＝90°∴∠DGC＝90°，∵四边形ABCD为正方形

∴∠ADC＝90°，AD＝CD，∵∠ADE+∠2＝90°，∴∠1+∠2＝90°，∴∠1＝∠ADE，∵l3∥l4，∴∠1＝∠DCG，∠ADE＝∠DCG，

ABCD为“格线四边形”，其长：

1，EG过正方形ABCD的顶点D且垂直l1于点E，分别交l2，l4于点F，G．将∠AEG绕点

2：

1，求矩形ABCD的宽．

2），点D′在直线l3上，以AD′为边在E′D′左侧作菱形

在△AED与△DGC中，

，∴△AED≌△GDC

AAS），

∴AE＝GD＝1，ED＝GC＝3，∴AD＝＝，

故答案为：

；

（2）如图2过点B作BE⊥L1于点E，反向延长则BE＝1，BF＝3，

∵四边形ABCD是矩形，∴∠ABC＝90°，∴∠∵∠ABE+∠EAB＝90°，∴∠FBC＝∠EAB，

BE交L4于点

F，

ABE+∠FBC＝90°，

当AB

BC，∴AE＝

BF＝

∴AB＝

如图3当AB>BC时，

同理可得：

BC＝

l3于点O，N，

，

；

，

；

∴矩形的宽为：

E′作ON垂直于l1分别交l1，，则∠E′FN＝60°

（3）如图4过点∵∠OAE′＝30°

∵AE′＝AE＝1，

故E′O＝

，E′N＝

E′

D′

由勾股定理可知菱形的边长为：

10．四边形ABCD是边长为4的正方形，点E在边AD所在直线上，（点D，点F在直线CE的同侧），连接BF．

连接CE，以CE为边，作正方形CEFG

（1）如图1，当点E与点A重合时，请直接写出BF的长；

（2）如图2，当点E在线段AD上时，AE＝1；

1求点F到AD的距离；

2求BF的长；

（3）若BF＝3，请直接写出此时AE的长．

【解答】解：

（1）作FH⊥AB于H，如图

∵四边形ABCD和四边形CEFG是正方形，∴AD＝CD＝4，EF＝CE，∠ADC＝∠DAH＝∠BAD＝∠CEF＝90°，

∴∠FEH＝∠CED，

在△EFH和△CED中，

，

∴△EFH≌△CED（AAS），

∴FH＝CD＝4，AH＝AD＝4，∴BH＝AB+AH＝8，

∴BF＝＝＝4；

2）过F作FH⊥AD交AD的延长线于点H，作FM⊥AB于M，如图2所示：

则FM＝AH，AM＝FH，

①∵AD＝4，AE＝1，∴DE＝3，同

（1）得：

△EFH≌△CED（AAS），∴FH＝DE＝3，EH＝CD＝4，即点F到AD的距离为3；

②∴BM＝AB+AM＝4+3＝7，FM＝AE+EH＝5，

3）分三种情况：

①当点E在边AD的左侧时，过F作FH⊥AD交AD于点H，交BC延长线于K．如图3所示：

同

（1）得：

△EFH≌△CED，

∴FH＝DE＝AE+4，EH＝CD＝4，

∴FK＝8+AE，在Rt△BFK中，BK＝AH＝EH﹣AE＝4﹣AE，由勾股定理得：

（4﹣AE）2+（8+AE）2＝（3）2，

解得：

AE＝1或AE＝﹣5（舍去），

∴AE＝1；②当点E在边AD的右侧时，过F作FH⊥AD交AD的延长线于点

同理得：

AE＝2+或2﹣（舍去）．

3当点E在AD上时，可得：

（8﹣AE）2+（4+AE）2＝90，解得AE＝5或﹣1，

5>4不符合题意．

综上所述：

AE的长为1或2+．