最新高等数学下册期末考试试题含答案OZ.docx

最新高等数学下册期末考试试题含答案OZ.docx

《最新高等数学下册期末考试试题含答案OZ.docx》由会员分享，可在线阅读，更多相关《最新高等数学下册期末考试试题含答案OZ.docx（20页珍藏版）》请在冰豆网上搜索。

最新高等数学下册期末考试试题含答案OZ

2019最新高等数学（下册）期末考试试题（含答案）

一、解答题

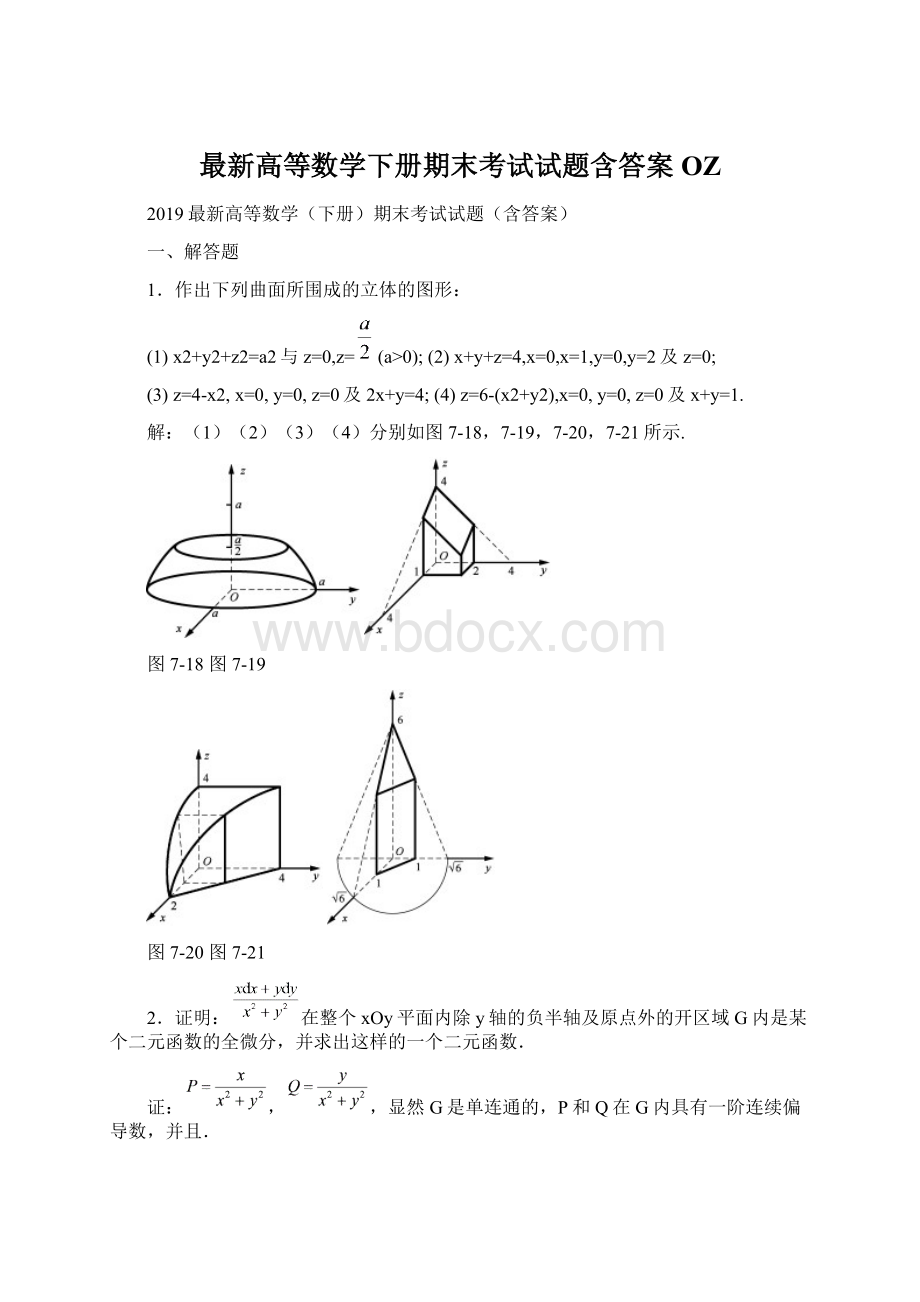
1．作出下列曲面所围成的立体的图形：

（1）x2+y2+z2=a2与z=0,z=（a>0）;

（2）x+y+z=4,x=0,x=1,y=0,y=2及z=0;

（3）z=4-x2,x=0,y=0,z=0及2x+y=4;（4）z=6-（x2+y2）,x=0,y=0,z=0及x+y=1.

解：

（1）

（2）（3）（4）分别如图7-18，7-19，7-20，7-21所示.

图7-18图7-19

图7-20图7-21

2．证明：

在整个xOy平面内除y轴的负半轴及原点外的开区域G内是某个二元函数的全微分，并求出这样的一个二元函数．

证：

，，显然G是单连通的，P和Q在G内具有一阶连续偏导数，并且．

，（x,y）∈G

因此在开区域G内是某个二元函数u（x,y）的全微分．

由

知．

3．证明下列曲线积分与路径无关，并计算积分值：

（1）；

（2）；

（3）沿在右半平面的路径；

（4）沿不通过原点的路径；

证：

（1）P=x-y，Q=y-x．显然P，Q在xOy面内有连续偏导数，且，故积分与路径无关．取L为从（0,0）到（1,1）的直线段，则L的方程为：

y=x，x：

0→1．于是

（2）P=6xy2-y3，Q=6x2y-3xy2．显然P，Q在xOy面内有连续偏导数，且，，有，所以积分与路径无关．

取L为从（1,2）→（1,4）→（3,4）的折线，则

（3），，P，Q在右半平面内有连续偏导数，且，，在右半平面内恒有，故在右半平面内积分与路径无关．

取L为从（1,1）到（1,2）的直线段，则

（4），，且在除原点外恒成立，故曲线积分在不含原点的区域内与路径无关，

取L为从（1,0）→（6,0）→（6,8）的折线，则

4．设L为xOy面内直线x=a上的一段，证明：

其中P（x,y）在L上连续．

证：

设L是直线x=a上由（a,b1）到（a,b2）这一段，

则L：

，始点参数为t=b1，终点参数为t=b2故

5．指出下列各微分方程的阶数：

（1）一阶

（2）二阶

（3）三阶

（4）一阶

6．利用高斯公式，计算下列曲面积分：

（1），其中Σ为平面x=0，y=0，z=0，x=a，y=a，z=a所围成的立体的表面的外侧；

（2），其中Σ为球面x2+y2+z2=a2的外侧；

（3），其中Σ为上半球体x2+y2≤a2，的表面外侧；

（4），其中Σ是界于z=0和z=3之间的圆柱体x2+y2=9的整个表面的外侧；

解：

（1）由高斯公式

（2）由高斯公式：

（3）由高斯公式得

（4）由高斯公式得：

7．设某流体的流速V=（k,y,0），求单位时间内从球面x2+y2+z2=4的内部流过球面的流量.

解：

设球体为Ω，球面为Σ，则流量

（由高斯公式）

8．求底面半径相等的两个直交圆柱面x2+y2=R2及x2+z2=R2所围立体的表面积。

解：

由对称性知，所围立体的表面积等于第一卦限中位于圆柱面x2+y2=R2内的部分面积的16倍，如图10-30所示。

图10-30

这部分曲面的方程为，于是所求面积为.

9．利用球面坐标计算下列三重积分：

（1），其中Ω是由球面所围成的闭区域；

（2），其中Ω由不等式,所确定.

解：

（1）

（2）积分区域Ω如图10-50所示，在球面坐标系下，Ω可表示为

故

10．画出积分区域，改变累次积分的积分次序：

（1）;

（2）;

（3）;（4）;

（5）.

解：

（1）相应二重保健的积分区域为D：

如图10-6所示.

图10-6

D亦可表示为：

所以

（2）相应二重积分的积分区域D：

如图10-7所示.

图10-7

D亦可表示为：

所以

（3）相应二重积分的积分区域D为：

如图10-8所示.

图10-8

D亦可看成D1与D2的和，其中

D1：

D2：

所以.

（4）相应二重积分的积分区域D为：

如图10-9所示.

图10-9

D亦可看成由D1与D2两部分之和，其中

D1：

D2：

所以

（5）相应二重积分的积分区域D由D1与D2两部分组成，其中

D1：

D2：

如图10-10所示.

图10-10

D亦可表示为：

所以

11．求函数u=xy2+z3-xyz在点（1，1,2）处沿方向角为的方向导数。

解：

12．设，试求

解：

由方程组

可确定反函数，方程组两边对x求导，得

解得

所以

方程组两边对y求导，得

解得

所以.

13．求下列函数在给定点和自变量增量的条件下的全增量和全微分：

（1）

（2）

解：

（1）

（2）

14．求下列各微分方程满足所给初始条件的特解：

;

解：

令，则,

原方程可化为

由知，，从而有

由,得

故或.

;

解：

令，则.

原方程可化为

则

以代入上式得

则

当x=1时，y=0代入得

故所求特解为.

;

解：

当，得

以x=0,y=0代入上式得

故所求特解为.

;

解：

令，则.

原方程可化为

以代入上式得.

以x=0,y=1代入上式得

故所求特解为

;

解：

令，则.

原方程可化为

即

积分得

以代入上式得,

则

以x=0,y=0代入得，

故所求特解为

即.即.

.

解：

令

原方程可化为

以代入得

故

由于.故，即

积分得

以x=0,y=1代入得

故所求特解为.

15．求下列曲面和直线的交点：

（1）与;

（2）与.

解：

（1）直线的参数方程为

代入曲面方程解得t=0,t=1.

得交点坐标为（3，4，-2），（6，-2，2）.

（2）直线的参数方程为

代入曲面方程可解得t=1,

得交点坐标为（4，-3，2）.

16．在空间直角坐标系中，定出下列各点的位置：

A（1,2,3）;B（-2,3,4）;C（2,-3,-4）;

D（3,4,0）;E（0,4,3）;F（3,0,0）.

解：

点A在第Ⅰ卦限；点B在第Ⅱ卦限；点C在第Ⅷ卦限；

点D在xOy面上；点E在yOz面上；点F在x轴上.

17．指出下列方程所表示的是什么曲面，并画出其图形：

（1）;

（2）;

（3）;（4）;

（5）;（6）.

解：

（1）母线平行于z轴的抛物柱面，如图7-7.

（2）母线平行于z轴的双曲柱面,如图7-8.

图7-7图7-8

（3）母线平行于y轴的椭圆柱面，如图7-9.

（4）母线平行于x轴的抛物柱面，如图7-10.

图7-9图7-10

（5）母线平行于z轴的两平面，如图7-11.

（6）z轴，如图7-12.

图7-11图7-12

18．试定出下列各题中直线与平面间的位置关系：

（1）和4x-2y-2z=3;

（2）和3x-2y+7z=8;

（3）和x+y+z=3.

解：

平行而不包含.因为直线的方向向量为s={-2，-7，3}

平面的法向量n={4，-2，-2}，所以

于是直线与平面平行.

又因为直线上的点M0（-3，-4，0）代入平面方程有.故直线不在平面上.

（2）因直线方向向量s等于平面的法向量，故直线垂直于平面.

（3）直线在平面上，因为,而直线上的点（2，-2，3）在平面上.

19．求下列直线与平面的交点：

（1）,2x+3y+z-1=0;

（2）,x+2y-2z+6=0.

解：

（1）直线参数方程为

代入平面方程得t=1

故交点为（2，-3，6）.

（2）直线参数方程为

代入平面方程解得t=0.

故交点为（-2，1，3）.

20．通过点（1，-1，1）作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.

解：

设所求平面方程为Ax+By+Cz+D=0

其法向量n={A,B,C}

n1={1,-1,1},n2={2,1,1}

又（1，－1，1）在所求平面上，故A－B+C+D=0，得D=0

故所求平面方程为

即2x-y-3z=0

21．通过两点（1，1，1，）和（2，2，2）作垂直于平面x+y-z=0的平面.

解：

设平面方程为Ax+By+Cz+D=0

则其法向量为n={A,B,C}

已知平面法向量为n1={1,1,-1}

过已知两点的向量l={1,1,1}

由题知n·n1=0,n·l=0

即

所求平面方程变为Ax-Ay+D=0

又点（1，1，1）在平面上，所以有D=0

故平面方程为x-y=0.

22．求过点M0（1,7,-3），且与连接坐标原点到点M0的线段OM0垂直的平面方程.

解：

所求平面的法向量可取为

故平面方程为：

x-1+7（y-7）-3（z+3）=0

即x+7y-3z-59=0

23．一动点与M0（1,1,1）连成的向量与向量n=（2,3,-4）垂直，求动点的轨迹方程.

解：

设动点为M（x,y,z）

因,故.

即2（x-1）+3（y-1）-4（z-1）=0

整理得：

2x+3y-4z-1=0即为动点M的轨迹方程.

24．解：

设四面体的底为，从点到底面的高为，则

，

而

又所在的平面方程为:

则

故

25．已知三点A（2,-1,5）,B（0,3,-2）,C（-2,3,1），点M，N，P分别是AB，BC，CA的中点，证明：

.

证明：

中点M，N，P的坐标分别为

故.

26．设向量的模是4，它与投影轴的夹角是60°，求这向量在该轴上的投影.

解：

设M的投影为，则

27．验证：

.

证明：

利用三角形法则得证.见图7-1

图7-1

28．试证：

以三点A（4，1，9），B（10，-1，6），C（2，4，3）为顶点的三角形是等腰直角三角形.

证明：

因为|AB|=|AC|=7.且有

|AC|2+|AB|2=49+49=98=|BC|2.

故△ABC为等腰直角三角形.

29．在z轴上，求与两点A（-4，1，7）和B（3，5，-2）等距离的点.

解：

设此点为M（0，0，z），则

解得

即所求点为M（0，0，）.

30．指出下列函数在向外间断：

（1）f（x,y）=;

（2）f（x,y）=;

（3）f（x,y）=ln（1－x2－y2）;（4）f（x,y）=

解：

（1）因为当y=-x时，函数无定义，所以函数在直线y=-x上的所有点处间断，而在其余点处均连续.

（2）因为当y2=2x时，函数无定义，所以函数在抛物线y2=2x上的所有点处间断.而在其余各点处均连续.

（3）因为当x2+y2=1时，函数无定义，所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续.

（4）因为点P（x,y）沿直线y=x趋于O（0,0）时.

.

故（0，0）是函数的间断点，而在其余各点处均连续.

【参考答案】***试卷处理标记，请不要删除

一、解答题

1．无

2．无

3．无

4．无

5．无

6．无

7．无

8．无

9．无

10．无

11．无

12．无

13．无

14．无

15．无

16．无

17．无

18．无

19．无

20．无

21．无

22．无

23．无

24．无

25．无

26．无

27．无

28．无

29．无

30．无