VerticalAsymptotes垂直渐近线.docx

VerticalAsymptotes垂直渐近线.docx

《VerticalAsymptotes垂直渐近线.docx》由会员分享，可在线阅读，更多相关《VerticalAsymptotes垂直渐近线.docx（16页珍藏版）》请在冰豆网上搜索。

VerticalAsymptotes垂直渐近线

VerticalAsymptotes：

垂直渐近线

VerticalAsymptotes

Verticalasymptotesareverticallineswhichcorrespondtothezeroesofthedenominatorofarationalfunction.（Theycanalsoariseinothercontexts,suchaslogarithms,butyou'llalmostcertainlyfirstencounterasymptotesinthecontextofrationals.）

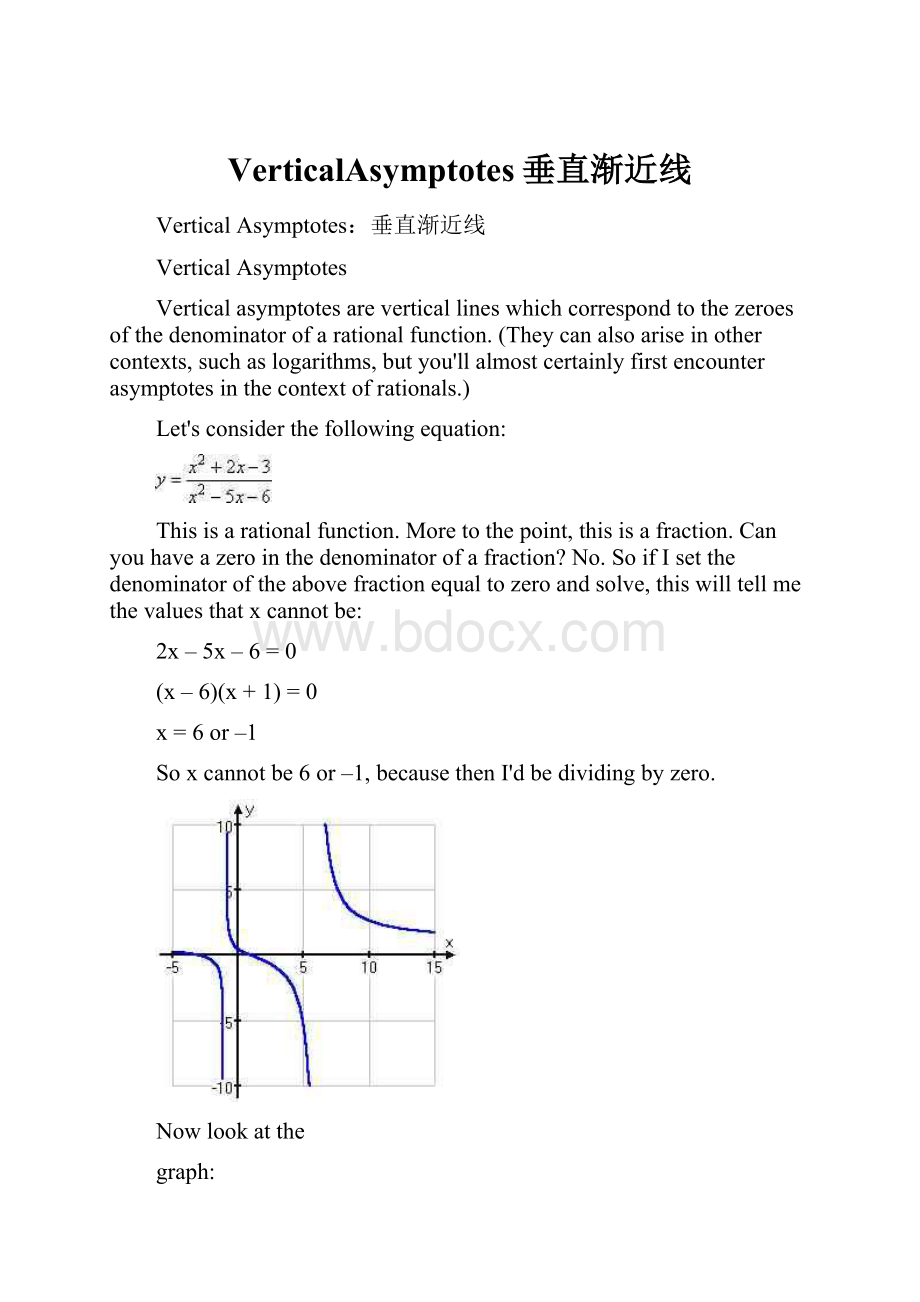
Let'sconsiderthefollowingequation:

Thisisarationalfunction.Moretothepoint,thisisafraction.Canyouhaveazerointhedenominatorofafraction?

No.SoifIsetthedenominatoroftheabovefractionequaltozeroandsolve,thiswilltellmethevaluesthatxcannotbe:

2x–5x–6=0

（x–6）（x+1）=0

x=6or–1

Soxcannotbe6or–1,becausethenI'dbedividingbyzero.

Nowlookatthe

graph:

Youcanseehowthegraphavoidedtheverticallinesx=6andx

=–1.Thisavoidanceoccurredbecausexcannotbe–1or6.In

otherwords,thefactthatthefunction'sdomainisrestrictedis

reflectedinthefunction'sgraph.Moreusefully,youcanusethe

domaintohelpyougraph,becausewhichevervaluesarenot

allowedinthedomainwillbeverticalasymptotesonthegraph.

Youcandrawthevertical

asymptoteasadashedlineto

remindyounottographthere,

likethis:

（It'salrightthatthegraph

appearstoclimbrightupthe

sidesoftheasymptoteonthe

left.Thisiscommon.Aslongas

youdon'tdrawthegraph

crossingtheverticalasymptote,

you'llbefine.）

Let'sreviewthisrelationshipbetweenthedomainandtheverticalasymptotes.

Findthedomainandverticalasymptotes（s）,ifany,of

thefollowingfunction:

Thedomainisthesetofallx-valuesthatI'mallowedtouse.

Theonlyvaluesthatcouldbedisallowedarethosethat

givemeazerointhedenominator.SoI'llsetthe

denominatorequaltozeroandsolve.

2x+2x–8=0

（x+4）（x–2）=0

x=–4orx=2

SinceIcan'thaveazerointhedenominator,thenIcan't

havex=–4orx=2inthedomain.Thistellsmethatthe

verticalasymptotes（whichtellmewherethegraphcannot

go）willbeatthevaluesx=–4orx=2.

domain:

verticalasymptotes:

x=–4,2

Notethatthedomainandverticalasymptotesare"opposites".Theverticalasymptotesareat–4and2,andthedomainis

everywherebut–4and2.Thisisalwaystrue.

Findthedomainandverticalasymptote（s）,ifany,ofthefollowingfunction:

Tofindthedomainandverticalasymptotes,I'llsetthedenominatorequaltozeroandsolve.Thesolutionswillbethevaluesthatarenotallowedinthedomain,andwillalsobetheverticalasymptotes.

2x+9=0

2x=–9

Oops!

Thatdoesn'tsolve!

Sotherearenozeroesinthedenominator.Sincetherearenozeroesinthedenominator,thentherearenoforbiddenx-values,andthedomainis"all

x".Also,sincetherearenovaluesforbiddentothedomain,therearenoverticalasymptotes.

domain:

allx

verticalasymptotes:

none

Noteagainhowthedomainandverticalasymptoteswere

"opposites"ofeachother.

Findthedomainandverticalasymptote（s）,ifany,of

thefollowingfunction:

I'llcheckthezeroesofthedenominator:

2x+5x+6=0

（x+3）（x+2）=0

x=–3orx=–2

SinceIcan'tdividebyzero,thenIhaveverticalasymptotes

atx=–3andx=–2,andthedomainisallotherx-values.

domain:

verticalasymptotes:

x=–3andx=–2

Whengraphing,rememberthatverticalasymptotesstandforx-

valuesthatarenotallowed.Verticalasymptotesaresacredground.Never,onpainofdeath,canyoucrossaverticalasymptote.Don'teventry!

Whereasverticalasymptotesaresacredground,horizontalasymptotesarejustusefulsuggestions.Whereasyoucannevertouchaverticalasymptote,youcan（andoftendo）touchandevencrosshorizontalasymptotes.Whereasverticalasymptotesindicateveryspecificbehavior（onthegraph）,usuallyclosetotheorigin,horizontalasymptotesindicategeneralbehaviorfarofftothesidesofthegraph.Togettheideaofhorizontalasymptotes,let'slooksatsomesimpleexamples.

Findthehorizontalasymptoteofthefollowingfunction:

Thehorizontalasymptotetellsme,roughly,wherethegraphwillgowhenxisreally,reallybig.SoI'lllookatsomeverybigvaluesforx,somevaluesofxveryfarfromthe

origin:

x

–100000–0.0000099...

–10000–0.0000999...

–1000–0.0009979...

–100–0.0097990...

–10–0.0792079...

–10.5

02

11.5

100.1188118...

1000.0101989...

10000.0010019...

100000.0001000...

1000000.0000100...

Offtothesidesofthegraph,wherexisstronglynegative（suchas–1,000）orstronglypositive（suchas10000）,the

"+2"andthe"+1"intheexpressionforyreallydon'tmattersomuch.Iendeduphavingareallybignumberdividedby

areallybignumbersquared,which"simplified"tobeavery

smallnumber.They-valuecamemostlyfromthe"x"and

222the"x".Andsincethexwas"bigger"thanthex,thex

draggedthewholefractiondowntoy=0（thatis,thex-axis）

whenxgotbig.

Icansee

this

behavior

onthe

graph:

Thegraphshowssomeslightlyinterestingbehaviorinthemiddle,neartheorigin,buttherestofthegraphisfairlyboring,trailingalongthex-axis.

IfIzoominontheorigin,Icanalsoseethatthegraphcrossesthehorizontalasymptote

（Itiscommonandperfectlyokaytocrossahorizontalasymptote.It'stheverticalasymptotesthatI'mnotallowedtotouch.）

AsIcanseeinthetableofvaluesandthegraph,thehorizontalasymptoteisthex-axis.

horizontalasymptote:

y=0（thex-axis）

Intheaboveexercise,thedegreeonthedenominator（namely,2）

wasbiggerthanthedegreeonthenumerator（namely,1）,and

thehorizontalasymptotewasy=0（thex-axis）.

Thispropertyisalwaystrue:

Ifthedegreeonxinthe

denominatorislargerthanthedegreeonxinthenumerator,

thenthedenominator,being"stronger",pullsthefractiondowntothex-axiswhenxgetsbig.Thatis,ifthepolynomialinthedenominatorhasabiggerleadingexponentthanthepolynomialinthenumerator,thenthegraphtrailsalongthex-axisatthefar

rightandthefarleftofthegraph.

Whathappensifthedegreesarethesameinthenumeratoranddenominator?

Findthehorizontalasymptoteofthefollowing:

Unlikethepreviousexample,thisfunctionhasdegree-2

polynomialstopandbottom;inparticular,thedegreesarethesameinthenumeratorandthedenominator.Sincethedegreesarethesame,thenumeratoranddenominator"pull"evenly;thisgraphshouldnotdragdowntothex-axis,norshoulditshootoff

toinfinity.Butwherewillitgo?

Again,Ineedtothinkintermsofbigvaluesforx.Whenxis

reallybig,I'llhave,roughly,twicesomethingbig（minusaneleven）dividedbyoncesomethingbig（plusanine）.Asyou

mightguessfromthelastexercise,the"–11"andthe"+9"won't

mattermuchforreallybigvaluesofx.Farofftothesidesofthe

22graph,I'llroughlyhave"2x/x",whichreducestojust2.Doesa

tableofvaluesbearthisout?

Let'scheck:

x

–1000001.9999999...

–100001.9999997...

–10001.9999710...

–1001.9971026...

–101.7339449...

–1–0.9

0–1.2222222...

1–0.9

101.7339449...

1001.9971026...

10001.9999710...

100001.9999997...

1000001.9999999...

Forbigvaluesofx,thegraphis,asexpected,verycloseto

y=2.

Thegraph

reflectsthis:

Thenmyansweris:

horizontalasymptote:

y=2

Intheexampleabove,thedegreesonthenumeratoranddenominatorwerethesame,andthehorizontalasymptoteturnedouttobethehorizontallinewhosey-valuewasequalto

thevaluefoundbydividingtheleadingcoefficientsofthetwopolynomials.Thisisalwaystrue:

Whenthedegreesofthenumeratorandthedenominatorarethesame,thenthehorizontalasymptoteisfoundbydividingtheleadingterms,sotheasymptoteisgivenby:

y=（numerator'sleadingcoefficient）/（denominator's

leadingcoefficient）

Whathappensifthedegreeisgreaterinthenumeratorthaninthedenominator?

Reasonably,thenumerator,being"stronger",oughtto"pull"thegraphawayfromthex-axis（y=0）oranyother

fixedy-value.

Toinvestigate,lookatthefollowingtable.Inthecolumntotheleftofthefirstgraph,youcanseetheoriginalfunction,theoriginalfunctionafterrearrangementbylongdivision,andthe

polynomial-onlypartoftheoriginalfunction.Thenlookatthesecondgraphinthesametable,andnotethesimilaritybetweenthegraphoftheoriginalfunctionandthegraphofthepolynomialpartofthefunction.

originalgraphoftheoriginal

function:

function:

longdivision:

rearranged

function:

graphofpolynomialpart:

polynomialpart:

y=–3x–3

Notethe

similarity

betweenthe

twographs.

Exceptfor

wherethe

vertical

asymptote

causesabreak

inthemiddle,

thetwographs

arepractically

thesame,as

youcansee

fromthe

overlay.

Thegraphsshowthat,ifthedegreeofthenumeratorisexactly

onemorethanthedegreeofthedenominator（sothatthe

polynomialfractionis"improper"）,thenthegraphoftherationalfunctionwillbe,roughly,aslant-ystraightlinewithsomefiddlybitsinthemiddle.Becausethegraphwillbenearlyequaltothisslantedstraight-lineequivalent,theasymptoteforthissortofrationalfunctioniscalleda"slant"（or"oblique"）asymptote.Theequationfortheslantasymptoteisthepolynomialpartoftherationalthatyougetafterdoingthelongdivision

（Bytheway,thisrelationship--betweenanimproperrationalfunction,itsassociatedpolynomial,andtheirgraphs--holdstrue

regardlessofthedifferenceinthedegreesofthenumeratoranddenominator.）

Findtheslantas