三级检验员焊接检验基础知识复习材料.docx
《三级检验员焊接检验基础知识复习材料.docx》由会员分享,可在线阅读,更多相关《三级检验员焊接检验基础知识复习材料.docx(21页珍藏版)》请在冰豆网上搜索。
三级检验员焊接检验基础知识复习材料
焊接工艺问答(强度及结构)
各种焊接接头都有不同程度的应力集中,当母材具有足够的塑性时,结构在静开车破坏之前就有显著的塑性变形,应力集中对其强度无影响。
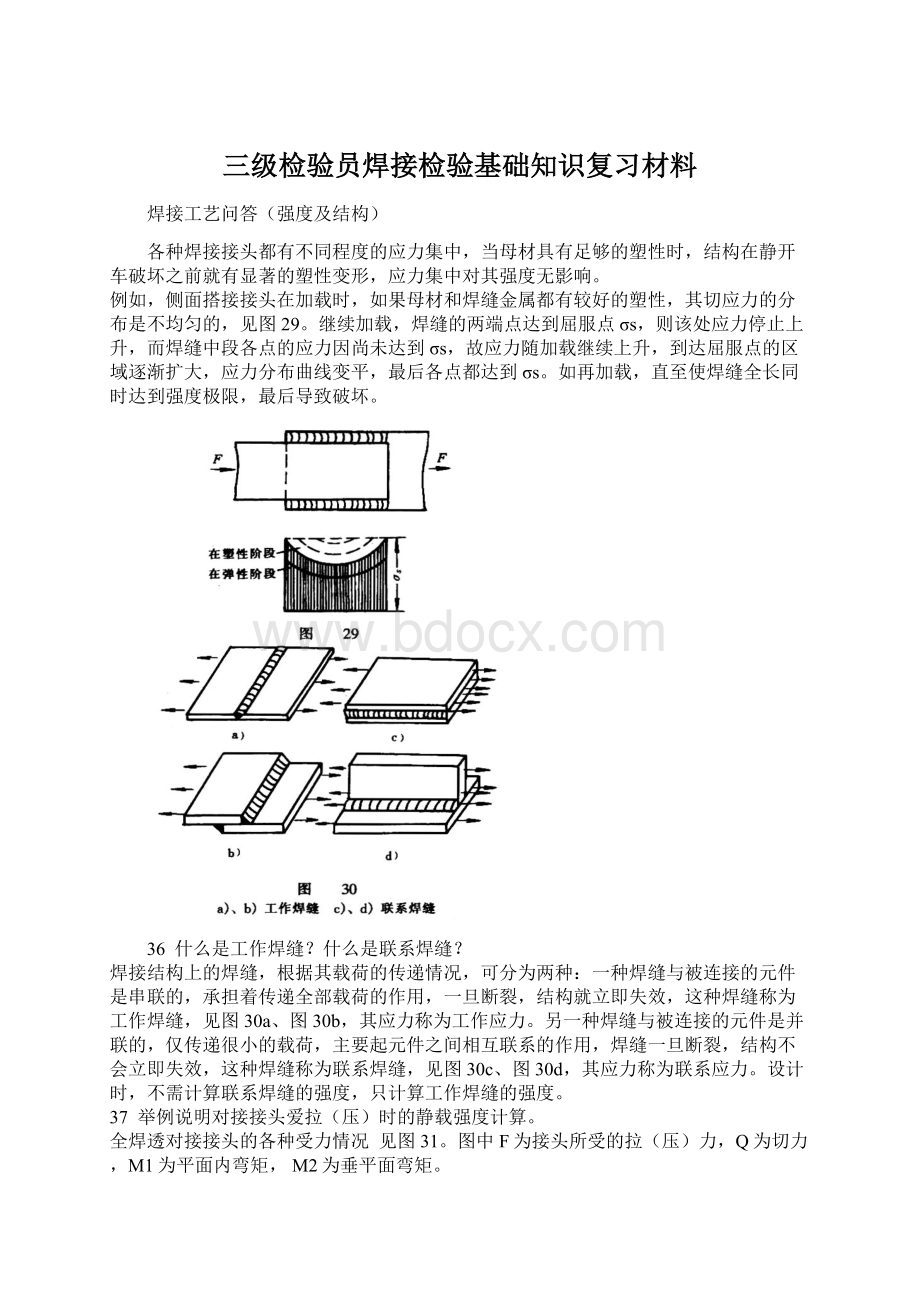
例如,侧面搭接接头在加载时,如果母材和焊缝金属都有较好的塑性,其切应力的分布是不均匀的,见图29。
继续加载,焊缝的两端点达到屈服点σs,则该处应力停止上升,而焊缝中段各点的应力因尚未达到σs,故应力随加载继续上升,到达屈服点的区域逐渐扩大,应力分布曲线变平,最后各点都达到σs。
如再加载,直至使焊缝全长同时达到强度极限,最后导致破坏。
36 什么是工作焊缝?
什么是联系焊缝?
焊接结构上的焊缝,根据其载荷的传递情况,可分为两种:
一种焊缝与被连接的元件是串联的,承担着传递全部载荷的作用,一旦断裂,结构就立即失效,这种焊缝称为工作焊缝,见图30a、图30b,其应力称为工作应力。
另一种焊缝与被连接的元件是并联的,仅传递很小的载荷,主要起元件之间相互联系的作用,焊缝一旦断裂,结构不会立即失效,这种焊缝称为联系焊缝,见图30c、图30d,其应力称为联系应力。
设计时,不需计算联系焊缝的强度,只计算工作焊缝的强度。
37 举例说明对接接头爱拉(压)时的静载强度计算。
全焊透对接接头的各种受力情况 见图31。
图中F为接头所受的拉(压)力,Q为切力,M1为平面内弯矩,M2为垂平面弯矩。
受拉时的强度计算公式为
F
σt=─── ≤〔σ′t 〕
Lδ1
F
受压时的强度计算公式为 σα=─── ≤〔σ′α〕
Lδ1
式中 F——接头所受的拉力或压力(N);
L——焊缝长度(cm);
δ1——接头中较薄板的厚度(cm);
σ——接头受拉(σt)或受压(σα)时焊缝中所承受的应力(N/cm2)㈠
〔σ′t 〕——焊缝受拉时的许用应力(N/cm2)
〔σ′α 〕——焊缝受压时的许用应力(N/cm2)
计算例题 两块板厚为5mm、宽为500mm的钢板对接焊在一起,两端受28400N的拉力,材料为Q235-A钢,试校核其焊缝强度。
解:
查表得〔σ′t 〕=14200N/cm2。
根据已知条件,在上述公式中,F=28400N,L=500mm=50cm,δ1=5mm=0.5cm,代入计算为
F 28400
σt=───=─────=1136N/cm2<14200N/cm2
Lδ1 50×0.5
∴ 该对接接头焊缝强度满足要求,结构工作安全。
38 举例说明对接接头受剪切时的静载强度计算。
受剪切时的强度计算公式为
Q
τ=─── ≤〔τ′〕
Lδ1
式中 Q——接头所受的切力(N);
L——焊缝长度(cm);
δ1——接头中较薄板的厚度(cm);
τ——接头焊缝中所承受的切应力(N/cm2);
〔τ′〕——焊缝许用切应力(N/cm2)
计算例题 两块板厚为10mm的钢板对接焊,焊缝受29300N的拉力,材料为Q235-A钢,试设计焊缝的长度(钢板宽度)。
解:
查表得〔τ′〕=9800N/cm2。
根据已知条件,在上述公式中,Q=29300N,δ1=10mm=1cm,代入计算为
Q 28400
L≥──────=──────=2.99cm=29.9mm
δ1〔τ′〕 1×9800
取L=30mm。
即当焊缝长度(板宽)为30mm时,该对接接头焊缝强度能满足要求。
39 举例说明对接接头受弯矩时的静载强度计算。
受水平板面内弯矩的强度计算公式为
6M1
σ= ──── ≤〔σ′t 〕
δ1L2
受垂直板面内弯矩的强度计算公式为
6M2
σ= ──── ≤〔σ′t〕
δ12L
式中 M1——水平板面内弯矩(N/cm2);
M2——垂直板面弯矩(N/cm2);
L——焊缝长度(cm);
δ1——接头中较薄板的厚度(cm);
σ——接头受弯矩作用时焊缝中所承受的应力(N/cm2);
〔σ′t〕——焊缝受弯时的许用应力(N/cm2)。
计算例题 两块厚度相同钢板的对接接头,材料为16MnR钢,钢板宽度为30mm,受垂直板面弯矩300000N·cm,试计算焊缝所需的厚度(板厚)。
解:
查表得〔σ′t〕=20100N/cm2。
根据已知条件,在上述公式中,M2=300000N·cm,L=300mm=30cm,代入计算为
取δ1=18mm,即当焊缝厚度(板厚)为18mm时,该对接接头焊缝强度能满足要求。
40 举例说明搭接接头受拉(压)时的静载强度计算。
各种搭接接头的受力情况,见图32。
三种焊缝的计算公式为
⑴正面搭接焊缝受拉(压)的计算公式为
F
τ= ──── ≤〔τ′〕
1.4KL
⑵侧面搭接焊缝受拉(压)的计算公式为
F
τ= ──── ≤〔τ′〕
1.4KL
⑶联合搭接焊缝受拉(压)的计算公式为
F
τ= ──── ≤〔τ′〕
0.7KΣL
式中 F——搭接接头受的拉(压)力(N);
K——焊脚尺寸(cm);
L——焊缝长度(cm);
ΣL——正、侧面焊缝总长(cm);
τ——搭接接头角焊缝受的切应力(N/cm2);
〔τ′〕——焊缝金属许用切应力(N/cm2);
计算例题 将100mm×10mm的角钢用角焊缝搭接在一块钢板上见图33。
受拉伸时要求与角钢等强度,试计算接头的合理尺寸K和L应该是多少?
解:
从材料手册查得角钢断面积S=19.2cm2;许用应力〔σ〕=16000N/cm2,焊缝许用应力〔τ′〕=10000N/cm2。
角钢的允许载荷为
〔F〕=S〔σ〕=19.2×16000=307200N
假定接头上各段焊缝中的切应力都达到焊缝许用切应力值,即て=〔τ′〕。
若取K=10mm,采用手弧焊,则所需的焊缝总长为
〔F〕 307200
ΣL=───────=───────── =43.9cm
0.7K〔て′〕 0.7×1×10000
角钢一端的正面角焊缝L3=100mm,则两侧焊缝总长度为339mm。
根据材料手册查得角钢的拉力作用线位置e=28.2mm,按杠杆原理,则侧面角焊缝L2应承受全部侧面角焊缝载荷的28.3%。
28.3
∴ L2=339×───=96mm
100
另外一侧的侧面角焊缝长度L1应该为
100-28.3
L1=339×──────=243mm
100
取L1=250mm,L2=100mm。
41 举例说明搭接接头受弯矩时的静载强度计算。
搭接接头受弯矩的情况,见图34a。
计算公式为
式中 M——作用在接头上的外加弯矩(N/cm2);
K——焊脚尺寸(cm);
H——搭接板宽度(cm);
〔τ′〕——焊脚的许用切应力(N/cm2))。
计算例题 由三面焊缝组成的悬臂搭接接头(图34),当焊缝总长为500mm,K=10mm时,在梁的端头作用一弯矩M=2800000N·cm,试验计算接头是否安全?
已知焊缝作用切应力〔τ′〕=10000N/cm2。
42 举例说明搭接接头受偏心载荷时的静载强度计算。
如果搭接接头承受的载荷是垂直X轴方向的偏心载荷F见图35,此时焊缝中既有由弯矩M=FL引起的切应力τM(由来1公式计算),又是有由切力Q=F引起的切应力τQ为
计算例题 一偏心受载的搭接接头(图35),已知焊缝长h=400mm,l0=100mm,焊脚尺寸K=10mm,外加载荷F=30000N,梁长L=100cm,试校核焊缝强度。
焊缝的许用切应力〔τ′〕=10000N/cm2。
解:
分别计算τM、τQ:
43 举例说明T形接头受平行于焊缝载荷时的静载强度计算。
T形接头及其受载荷的情况,见图36a。
如果接头开坡口并焊透,其强度按对接接头计算,焊缝金属截面等于母材截面(S=δh)。
如果接头开I形坡口,此时产生最大切应力的危险点在焊缝的最上端,该点同时作用有两个切应力:
一个是由M=FL引起的τM;另一个是由Q=F引起的τQ。
τM、τQ的
44 什么是焊接结构的疲劳断裂?
疲劳断裂的过程由三个阶段所组成:
1)在承受重复载荷的结构的应力集中部位产生疲劳裂纹(此时结构所受应力低于弹性极限)。
2)疲劳裂纹稳定扩展。
3)结构断裂。
据统计,由于疲劳而失效的金属结构,约占失效结构的90%。
焊接结构较其它结构(如铆接结构)更容易产生疲劳断裂,这是因为:
1)铆接结构的疲劳裂纹发展遇到钉孔或板层间隔会受阻,焊接结构由于其整体性,一旦产生裂纹,裂纹扩展不受阻止,直至整个构件断裂。
2)焊接连接不可避免地存在着产生应力集中的夹渣、气孔、咬边等缺陷。
3)焊缝区存在着很大的残余拉应力。
几个典型的焊接结构疲劳断裂事例见图37。
图37a为直升飞机起落架的疲劳断裂。
裂纹从应力集中很高的角接板尖端开始,该机飞行着陆2118交后发生破坏,属于低周疲劳。
图37b为载重汽车底架纵梁的疲劳断裂。
该梁板厚5mm,承受反复的弯曲应力,在角钢和纵梁的焊接处,因应力集中很高而产生疲劳裂纹而破坏,此时该车已运行30000km。
45 试述焊接接头形式对疲劳极限的影响。
焊接结构中,在接头部位由于具有不同的应力集中,将对接头的疲劳极限产生程度不同的不利影响。
⑴对接接头 对接接头从焊缝至母材的形状变化不大,应力集中比其它接头要小,所以在所有的接头形式中具有最高的疲劳极限。
但是过大的余高会增加应力集中,使疲劳极限下降。
⑵T形接头 这种接头由于在焊缝向基本金属过渡处有明显的截面变化,应力集中系数比对接接头的应力集中系数高,因此其疲劳极限远低于对接接头。
提高T形接头疲劳极限的根本措施是开坡口焊接和加工焊缝过渡区使之圆滑过渡。
⑶搭接接头 这是一种疲劳极限最低的接头形式,特别是在原来对接接头的基础上,增加盖板来进行“加强”,其结果适得其反,这种盖板非但没有起到“加强”作用,反而使原来疲劳极限较高的对接接头被大大地削弱了。
46 试述焊接缺陷对疲劳极限的影响。
焊接缺陷对焊接接头的疲劳极限产生重大的不利影响,这种不利影响与焊接缺陷的种类、尺寸、方向和位置有关。
片状缺陷(如裂纹、未熔合、未焊透)比带圆角的缺陷(如气孔、点状夹渣)影响大。
表面缺陷比内部缺陷影响大。
与作用力方向垂直的片状缺陷的影响比其它方向大。
位于残余拉应力区内的缺陷的影响比在残余应力区内的大;位于应力集中区内的缺陷(如焊趾裂纹)的影响比在均匀应力区中同样缺陷影响大。
咬边和