13常用求面积体积公式要点.docx

13常用求面积体积公式要点.docx

《13常用求面积体积公式要点.docx》由会员分享，可在线阅读，更多相关《13常用求面积体积公式要点.docx（18页珍藏版）》请在冰豆网上搜索。

13常用求面积体积公式要点

1-3常用求面积、体积公式

1-3-1平面图形面积

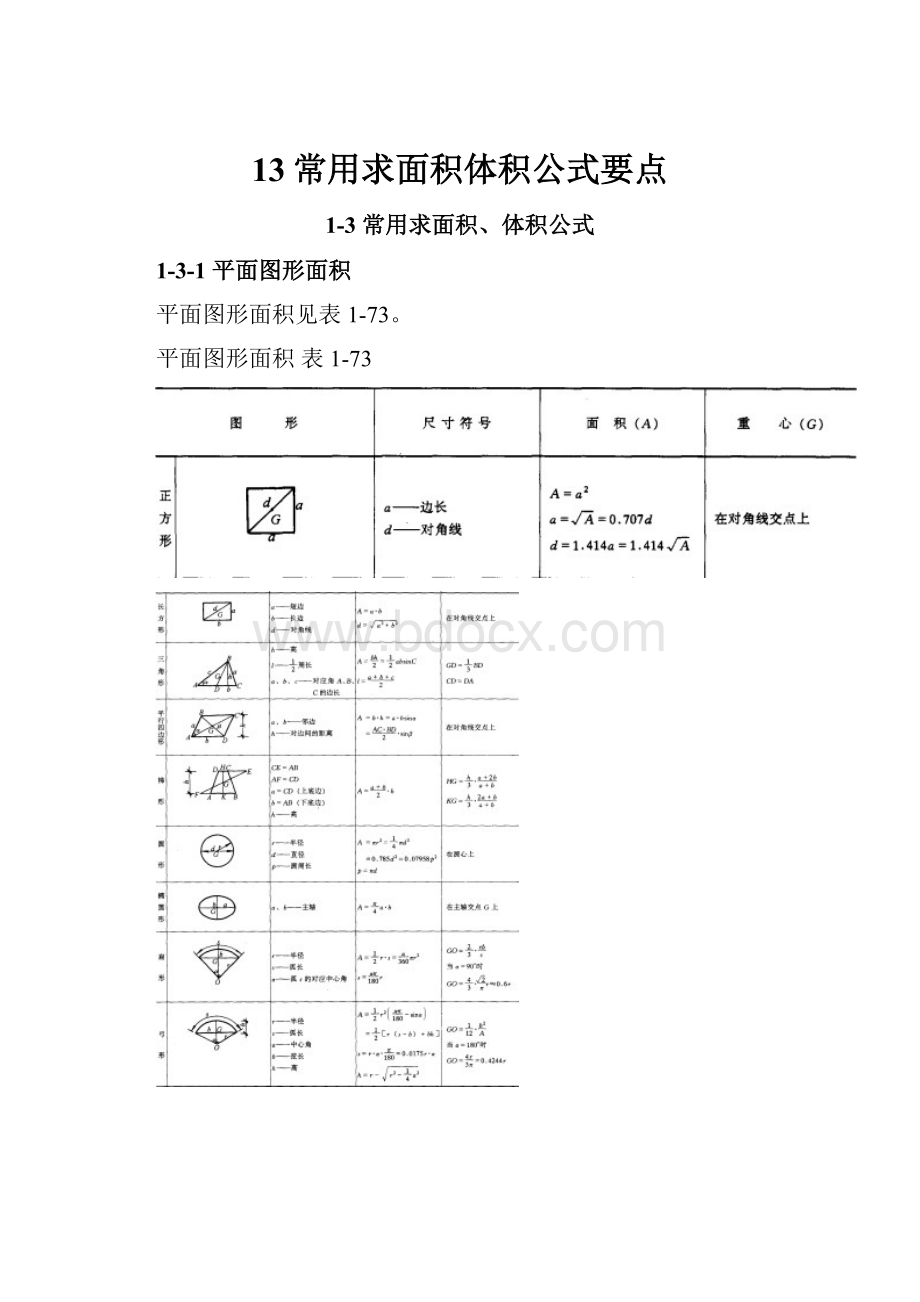
平面图形面积见表1-73。

平面图形面积表1-73

1-3-2多面体的体积和表面积

多面体的体积和表面积见表1-74。

多面体的体积和表面积表1-74

1-3-3物料堆体积计算

物料堆体积计算见表1-75。

物料堆体积计算表1-75

1-3-4壳体表面积、侧面积计算

1-3-4-1圆球形薄壳（图1-1）

图1-1圆球形薄壳计算图

1-3-4-2椭圆抛物面扁壳（图1-2）

图1-2椭圆抛物面扁壳计算图

1-3-4-3椭圆抛物面扁壳系数计算

见图1-2，壳表面积（A）计算公式：

A＝Sx·Sy＝2a×系数Ka×2b×系数Kb

式中Ka、Kb——椭圆抛物面扁壳系数，可按表1-76查得。

椭圆抛物面扁壳系数表表1-76

查表说明

［例］已知2a＝24.0m，2b＝16.0m，hx＝3.0m，hy＝2.8m，试求椭圆抛物面扁壳表面积A。

先求出hx/2a＝3.0/24.0＝0.125

hy/2b＝2.8/16.0＝0.175

分别查表得系数Ka为1.0402和系数Kb为1.0765，则扁壳表面积A＝24.0×1.0402×16.0×1.0765＝429.99m2

1-3-4-4圆抛物面扁壳（图1-3）

图1-3圆抛物面扁壳计算图

1-3-4-5单、双曲拱展开面积

1．单曲拱展开面积＝单曲拱系数×水平投影面积。

2．双曲拱展开面积＝双曲拱系数（大曲拱系数×小曲拱系数）×水平投影面积。

单、双曲拱展开面积系数见表1-77。

单双曲拱展开面积计算图见图1-4。

图1-4单、双曲拱展开面积计算图

L-拱跨；F-拱高

单、双曲拱展开面积系数表表1-77

//////////////////////////////////////////////////////////////////////////////////////////////

二、基坑土方工程量计算

（一）基坑土方量计算

  基坑土方量的计算，可近似地按拟柱体体积公式计算（图1—8）。

  图1—8基坑土方量计算      图1—9基坑土方量计算

    V=H*（A'+4A+A''）/6

  H——基坑深度（m）。

  A1、A2——基坑上下两底面积（m2）。

  A0——基坑中截面面积（m2）。

三、计算平整场地土方工程量

  ①四棱柱法

  A、方格四个角点全部为挖或填方时（图1—16），其挖方或填方体积为：

  式中：

h1、h2、h3、h4、——方格四个角点挖或填的施工高度，以绝对值带入（m）；

        a——  方格边长（m）。

图1—16角点全填或全挖；图1—17角点二填或二挖；图1—18角点一填三挖

  B、方格四个角点中，部分是挖方，部分是填方时（图1—17），其挖方或填方体积分别为：

  C、方格三个角点为挖方，另一个角点为填方时（图1—18），

  其填方体积为：

  其挖方体积为：

②三棱柱法

  计算时先把方格网顺地形等高线将各个方格划分成三角形（图1—19）

图1—19  按地形方格划分成三角形

  每个三角形的三个角点的填挖施工高度，用h1、h2、h3表示。

  A、当三角形三个角

  点全部为挖或填时（图1—20a），

  其挖填方体积为：

  式中：

a——方格边长（m）；

  h1、h2、h3——三角形各角点的施工

  高度，用绝对值（m）代入。

图1—20（a）三角棱柱体的体积计算（全挖或全填）

  B、三角形三个角点有挖有填时

  零线将三角形分成两部分，一个是底面为三角形的锥体，一个是底面为四边形的楔体（图1—20b，

图1—20（b）  三角棱柱体的体积计算（锥体部分为填方）

  其锥体部分的体积为：

  h1、h2、h3——三角形各角点的施工高度，取绝对值（m），h3指的是锥体顶点的施工高度。

  注意：

四方棱柱体的计算公式是根据平均中断面的近似公式推导而得的，当方格中地形不平时，误差较大，但计算简单，宜于手工计算。

三角棱柱体的计算公式是根据立体几何体积计算公式推导出来的，当三角形顺着等高线进行划分时，精确度较高，但计算繁杂，适宜用计算机计算。

  　　③断面法

  在地形起伏变化较大的地区，或挖填深度较大，断面又不规则的地区，采用断面法比较方便。

  方法：

沿场地取若干个相互平行的断面（可利用地形图定出或实地测量定出），将所取的每个断面（包括边坡断面），划分为若干个三角形和梯形，如图1—21，则面积：

图1—21  断面法

  断面面积求出后，即可计算土方体积，设各断面面积分别为：

  F1、F2、……Fn  相邻两断面间的距离依次为：

L1、L2、L3……Ln，则所求土方体积为：

（5）边坡土方量计算

  图1—22是场地边坡的平面示意图，从图中可以看出，边坡的土方量可以划分为两种近似的几何形体进行计算，一种为三角形棱锥体（如图中①②③  ……）另一种为三角棱柱体（如图中的④）

  A、三角形棱锥体边坡体积

  图1-22中①其体积为

  式中：

L1——边坡①的长度（m）；

  F1——边坡①的端面积（m2）；

  h2——角点的挖土高度；

  m——边坡的坡度系数。

  B、三角棱柱体边坡体积  

  如图中④其体积为

  当两端横断面面积相差很大的情况下：

  L——边坡④的长度（m）；

  F3、F5、F0——边坡④的两端及中部

//////////////////////////////////////////////////////////////////////////////////////////////////////////

一个好记并且好用的基坑计算公式

设基坑下底面积（含工作面）为S1

基坑上底面积（含工作面及放坡）为S2

深度为H

则基坑土方工程量V的计算公式为:

V=1/3*H*（S1+S2+S1与S2乘积的开方）

这个公式我用了近十年了,经过测试,它适用于长方形和正方形的各种基坑土方量计算,和你说的那个复杂公式计算结果基本相同

/////////////////////////////////////////

（基坑低面积+基坑口面积+根号下基坑低面积*基坑口面积）/3*深度=土方工程量

这是个万能公式，计算台体的。

。

。

。

。

。

。

。

。

。

PS:

土方是个大量，计算时不需要十分准确，可以近视为矩形

////////////////////////////////////////////

土石方工程量计算公式

土石方工程

一、人工平整场地:

S=S底+2*L外+16

二、挖沟槽:

1.垫层底部放坡:

V=L*（a+2c+kH）*H

2.垫层表面放坡

V=L*{（a+2c+KH1）H1+（a+2c）H2}

三、挖基坑（放坡）

方形:

V=（a+2c+KH）*（b+2c+KH）*H+1/3*K2H3

圆形:

V=∏/3*h*（R2+Rr+r2）

放坡系数

类别放坡起点人工挖土机械挖土

坑内作业坑上作业

一、二类别1.201：

0.51：

0.331：

0.75

三类土1.501：

0.331：

0.251：

0.67

四类土2.001：

0.251:

0.101：

0.33

一、基坑土方工程量计算

（一）基坑土方量计算

    基坑土方量的计算，可近似地按拟柱体体积公式计算（图1—8）。

    图1—8基坑土方量计算        图1—9基坑土方量计算

    V=H*（A'+4A+A''）/6

    H——基坑深度（m）。

    A1、A2——基坑上下两底面积（m2）。

    A0——基坑中截面面积（m2）。

二、计算平整场地土方工程量

    ①四棱柱法

    A、方格四个角点全部为挖或填方时（图1—16），其挖方或填方体积为：

    式中：

h1、h2、h3、h4、——方格四个角点挖或填的施工高度，以绝对值带入（m）；

            a——  方格边长（m）。

图1—16角点全填或全挖；图1—17角点二填或二挖；图1—18角点一填三挖

    B、方格四个角点中，部分是挖方，部分是填方时（图1—17），其挖方或填方体积分别为：

    C、方格三个角点为挖方，另一个角点为填方时（图1—18），

    其填方体积为：

    其挖方体积为：

②三棱柱法

    计算时先把方格网顺地形等高线将各个方格划分成三角形（图1—19）

图1—19  按地形方格划分成三角形

    每个三角形的三个角点的填挖施工高度，用h1、h2、h3表示。

    A、当三角形三个角

    点全部为挖或填时（图1—20a），

    其挖填方体积为：

    式中：

a——方格边长（m）；

    h1、h2、h3——三角形各角点的施工

    高度，用绝对值（m）代入。

图1—20（a）三角棱柱体的体积计算（全挖或全填）

    B、三角形三个角点有挖有填时

    零线将三角形分成两部分，一个是底面为三角形的锥体，一个是底面为四边形的楔体（图1—20b，

图1—20（b）  三角棱柱体的体积计算（锥体部分为填方）

    其锥体部分的体积为：

    h1、h2、h3——三角形各角点的施工高度，取绝对值（m），h3指的是锥体顶点的施工高度。

    注意：

四方棱柱体的计算公式是根据平均中断面的近似公式推导而得的，当方格中地形不平时，误差较大，但计算简单，宜于手工计算。

三角棱柱体的计算公式是根据立体几何体积计算公式推导出来的，当三角形顺着等高线进行划分时，精确度较高，但计算繁杂，适宜用计算机计算。

    　　③断面法

    在地形起伏变化较大的地区，或挖填深度较大，断面又不规则的地区，采用断面法比较方便。

    方法：

沿场地取若干个相互平行的断面（可利用地形图定出或实地测量定出），将所取的每个断面（包括边坡断面），划分为若干个三角形和梯形，如图1—21，则面积：

图1—21  断面法

    断面面积求出后，即可计算土方体积，设各断面面积分别为：

    F1、F2、……Fn  相邻两断面间的距离依次为：

L1、L2、L3……Ln，则所求土方体积为：

（5）边坡土方量计算

    图1—22是场地边坡的平面示意图，从图中可以看出，边坡的土方量可以划分为两种近似的几何形体进行计算，一种为三角形棱锥体（如图中①②③  ……）另一种为三角棱柱体（如图中的④）

    A、三角形棱锥体边坡体积

    图1-22中①其体积为

    式中：

L1——边坡①的长度（m）；

    F1——边坡①的端面积（m2）；

    h2——角点的挖土高度；

    m——边坡的坡度系数。

    B、三角棱柱体边坡体积    

    如图中④其体积为

    当两端横断面面积相差很大的情况下：

    L——边坡④的长度（m）；

    F3、F5、F0——边坡④的两端及中部横短面面积