最短路径问题Dijkstra算法和最小生成树Kruskal算法和Prim算法.docx
《最短路径问题Dijkstra算法和最小生成树Kruskal算法和Prim算法.docx》由会员分享,可在线阅读,更多相关《最短路径问题Dijkstra算法和最小生成树Kruskal算法和Prim算法.docx(12页珍藏版)》请在冰豆网上搜索。
最短路径问题Dijkstra算法和最小生成树Kruskal算法和Prim算法
上机实验1、2
1.最短路径问题(Dijkstra算法)
2.最小生成树(Kruskal算法和Prim算法)
一、最短路径问题(Dijkstra算法)
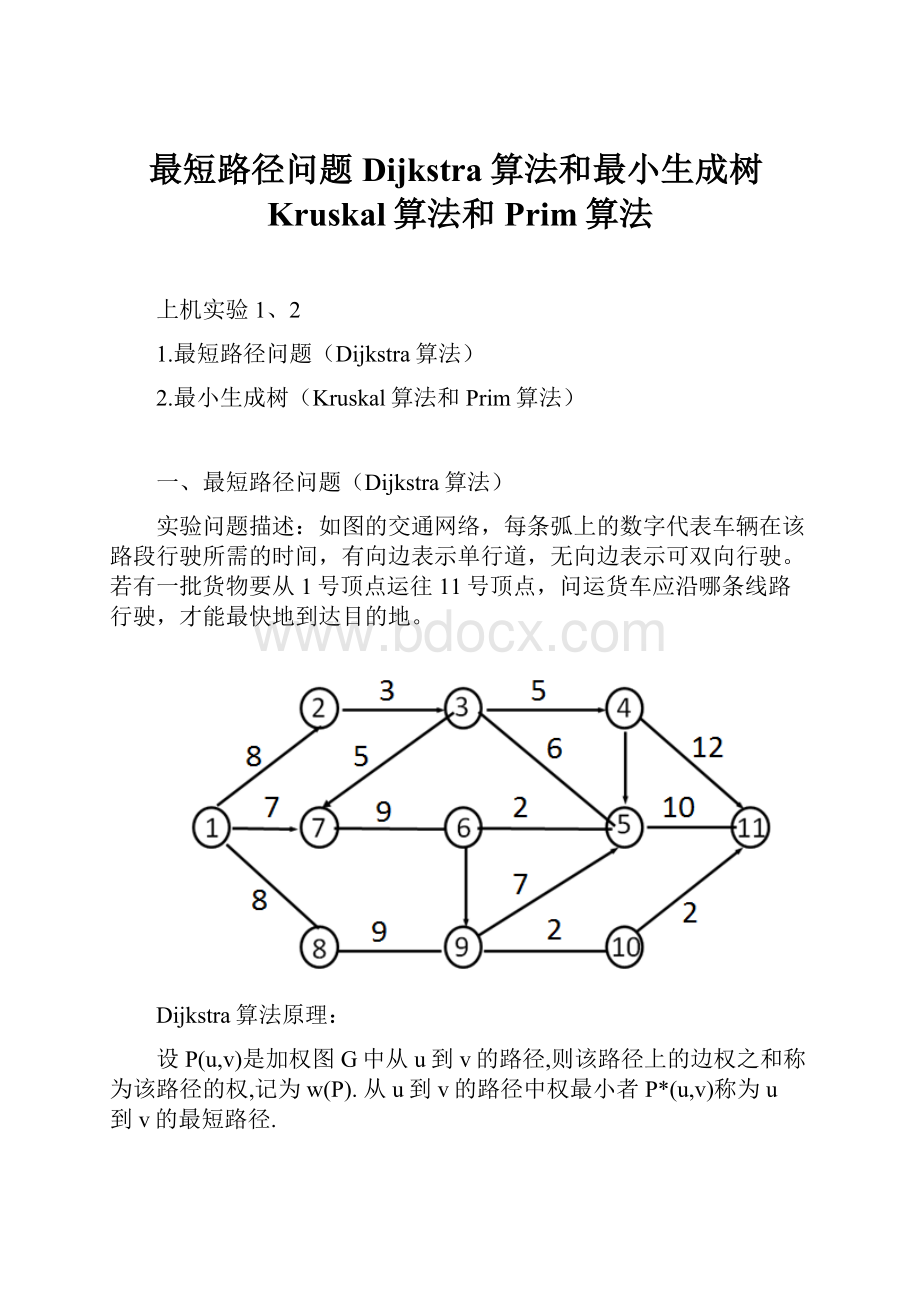
实验问题描述:
如图的交通网络,每条弧上的数字代表车辆在该路段行驶所需的时间,有向边表示单行道,无向边表示可双向行驶。
若有一批货物要从1号顶点运往11号顶点,问运货车应沿哪条线路行驶,才能最快地到达目的地。
Dijkstra算法原理:
设P(u,v)是加权图G中从u到v的路径,则该路径上的边权之和称为该路径的权,记为w(P).从u到v的路径中权最小者P*(u,v)称为u到v的最短路径.
当图中所有途径的权都不小于0时,目前公认最好的方法是由Dijkstra于1959年提出来的。
Dijkstra方法的基本思想是从
出发,逐步地向外探寻最短路。
执行过程中,与每个点对应,记录下一个数(称为这个点的标号),它或者表示从
到该点的最短路的权(称为P标号),或者表示从
到该点的最短路的权的上界(称为T标号),方法的每一步是去修改T标号,并且把某一个具T标号的点改变为具P标号的点,从而使图中具P标号的顶点数多一个,这样,至多经过p-1步,就可以求出从
到各点的最短路。
Dijkstra算法步骤:
S:
具有永久标号的顶点集;
l(v):
v的标记;f(v):
v的父顶点,用以确定最短路径;输入加权图的带权邻接矩阵w=[w(vi,vj)]nxm
1、初始化:
令l(v0)=0,S=
;
v
v0,l(v)=
;
2、更新l(v),f(v):
寻找不在S中的顶点u,使l(u)为最小.把u加入到S中,然后对所有不在S中的顶点v,如l(v)>l(u)+w(u,v),则更新l(v),f(v),即l(v)
l(u)+w(u,v),f(v)
u;
3、重复步骤2),直到所有顶点都在S中为止。
实验程序:
function[min,path]=dijkstra(w,start,terminal)
n=size(w,1);
label(start)=0;
f(start)=start;
fori=1:
n
ifi~=start
label(i)=inf;
end,end
s
(1)=start;u=start;
whilelength(s)fori=1:
n
ins=0;
forj=1:
length(s)
ifi==s(j)
ins=1;
end,end
ifins==0
v=i;
iflabel(v)>(label(u)+w(u,v))
label(v)=(label(u)+w(u,v));f(v)=u;
end,end,end
v1=0;
k=inf;
fori=1:
n
ins=0;
forj=1:
length(s)
ifi==s(j)
ins=1;
end,end
ifins==0
v=i;
ifk>label(v)
k=label(v);v1=v;
end,end,end
s(length(s)+1)=v1;
u=v1;
end
实验结果:
>>edge=[2,3,1,3,3,5,4,4,1,7,6,6,5,5,11,1,8,6,9,10,8,9,9,10;...
3,4,2,7,5,3,5,11,7,6,7,5,6,11,5,8,1,9,5,11,9,8,10,9;...
3,5,8,5,6,6,1,12,7,9,9,2,2,10,10,8,8,3,7,2,9,9,2,2];
n=11;weight=inf*ones(n,n);
fori=1:
n
weight(i,i)=0;
end
fori=1:
size(edge,2)
weight(edge(1,i),edge(2,i))=edge(3,i);
end
[dis,path]=dijkstra(weight,1,11)
dis=
21
path=
1891011
因此顶点1到顶点11的最短路径为1→8→9→10→11,其长度为21。
一、最小生成树(Kruskal算法和Prim算法)
实验问题描述:
Kruskal算法原理:
Kruskal算法的基本思想:
设一个有n个顶点的连通图G=(V,E),最初先构造一个只有n个顶点,但没有变的非连通图T={V,
},图中每个顶点自成一个联通分量。
在E中选一条权值最小的边,若改变的两个顶点落在不同的连通分量上,则将词便加入到T中;否则将此边舍去,重新选择一条权值最小的边,直到所有顶点落在同一个连通分量上。
算法步骤:
选择边
,使权w(
)最小(最大);
若已选定
,
,…
,则从E\{
,
,…
}中选取边
,使
(a)G[{
,
,…
}
{
}]无圈;
(b)权w(
)是满足(a)的最小(最大)者。
重复
,直到选取了n-1条边
Prim算法的基本思想:
从连通图G=(V,E)的某一顶点出发,选择与其关联的具有最小权值的边(
,
),将其顶点加入到生成树的顶点集合U中,以后每一步从一个顶点在U中而另一个顶点不在U中的个条边中选择权值最小的边(
),把它的顶点加入到集合U中,如此下去,直到图中的所有顶点都加入到生成树顶点集合U中为止,这是得到一棵最小生成树,一下就是Prim算法构造最小生成树的基本思想。
Kruskal算法程序:
function[Tc]=Krusf(d,flag)%d是图权值矩阵的一种表示方法,该矩阵每一列三个数表示图上一条边上的十点,终点和该边的权值
%T表示生成树德边集合,c表示生成树德权和
ifnargin==1
n=size(d,2);
m=sum(sum(d~=0))/2;
b=zeros(3,m);
k=1;
fori=1:
n
forj=(i+1):
n
ifd(i,j)~=0
b(1,k)=i;b(2,k)=j;
b(3,k)=d(i,j);k=k+1;
end
end
end
else
b=d;
end
n=max(max(b(1:
2,:
)));
m=size(b,2);
[B,i]=sortrows(b',3);
B=B';
c=0;T=[];
k=1;t=1:
n;
fori=1:
m
ift(B(1,i))~=t(B(2,i))
T(1:
2,k)=B(1:
2,i);
c=c+B(3,i);
k=k+1;
tmin=min(t(B(1,i)),t(B(2,i)));
tmax=max(t(B(1,i)),t(B(2,i)));
forj=1:
n
ift(j)==tmax
t(j)=tmin;
end
end
end
ifk==n
break;
end
end
T;
c;
Prim算法程序:
function[Tc]=Primf(a)
%a表示权值矩阵
%c表示生成树的权和
%T表示生成树的边集合
l=length(a);
a(a==0)=inf;
k=1:
l;
listV(k)=0;
listV
(1)=1;
e=1;
while(emin=inf;
fori=1:
l
iflistV(i)==1
forj=1:
l
iflistV(j)==0&min>a(i,j)
min=a(i,j);b=a(i,j);
s=i;d=j;
end
end
end
end
listV(d)=1;
distance(e)=b;
source(e)=s;
destination(e)=d;
e=e+1;
end
T=[source;destination];
c=0;
forg=1:
e-1
m(g)=a(T(1,g),T(2,g));
c=c+m(g);
end
c;
实验结果:
例4.17解
>>b=[1111112223344455;2345673574756767;185374610729456910];
>>[T,c]=Krusf(b,1)
T=
131144
245756
c=
19
>>b=[1111112223344455;2345673574756767;185374610729456910];
>>[Tc]=Primf(b)
T=
111544
257436
c=
19
从两种方法得到的最小生成树不同,但权和都为19
例4.18解:
>>a=[11122334;23435455;53784162];
>>[T,c]=Krusf(a,1)
T=
3412
4535
c=
10
>>a=[0537inf;508inf4;38016;7inf102;inf4620];
>>[Tc]=Primf(a)
T=
1345
3452
c=
10
从两种方法得到的最小生成树不同,但权和都为10
实验感想:
通过这两次的上机实验,我学习了利用计算机编程对最短路径问题和最小生成树问题进行求解。
此前在做数学实验过程中有自学Dijkstra算法,深刻地体会到该算法的优越性以及普适性,它很高效解决了现实生活中的最短路问题,是一个非常经典的算法。
这次学了Kruskal算法和Prim算法,对matlab有了新的理解与掌握,我对图论中的编程求解能力有了一定的提高。