凸轮连杆机构课程设计.docx
《凸轮连杆机构课程设计.docx》由会员分享,可在线阅读,更多相关《凸轮连杆机构课程设计.docx(17页珍藏版)》请在冰豆网上搜索。
凸轮连杆机构课程设计
第一章固定凸轮连杆机构参数选取
1.确定驱动方案
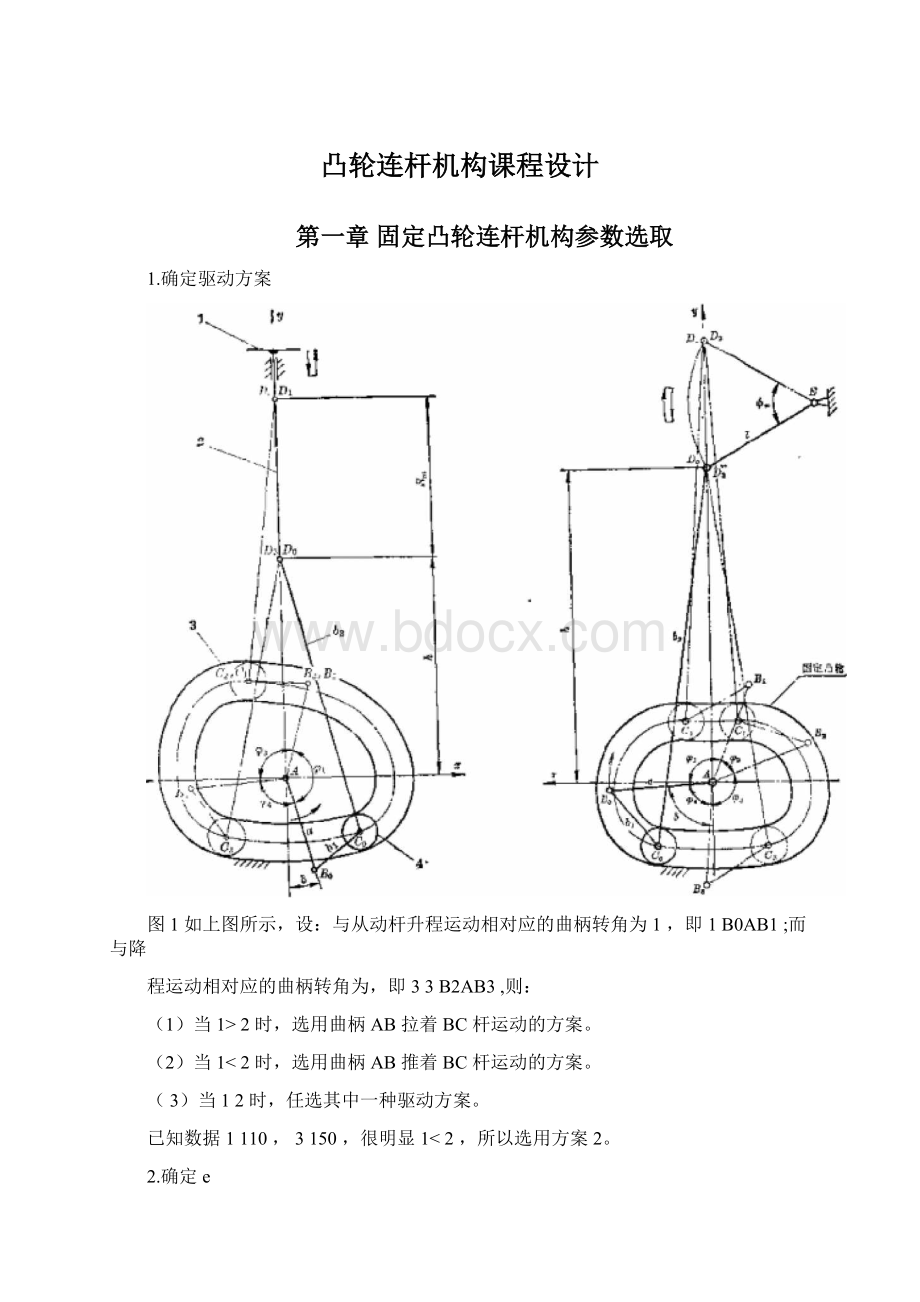
图1如上图所示,设:
与从动杆升程运动相对应的曲柄转角为1,即1B0AB1;而与降
程运动相对应的曲柄转角为,即33B2AB3,则:
(1)当1>2时,选用曲柄AB拉着BC杆运动的方案。
(2)当1<2时,选用曲柄AB推着BC杆运动的方案。
(3)当12时,任选其中一种驱动方案。
已知数据1110,3150,很明显1<2,所以选用方案2。
2.确定e
直动从动杆,取e0~0.2Sm,取e0
3.确定h
从结构紧凑和减小凸轮压力角考虑,应将h值取小些。
但h值愈小,对从动杆驱动力的压力角也愈大。
通常取hSm,去h120mm
4.确定a
a=0.6~0.9Sm或
若a值过小,会使凸轮压力角明显增大,甚至不能实现预期动动。
可取
m
a=1.2~1.8lsinm。
取a=70mm
2
6、确定
其值对凸轮的压力角影响极大,过小,尤其是过大,会使压力角急剧增加。
在前述参
数确定后,最好将优化,目标函数为
a1m()(a1m)min
式中a1m为凸轮的最大压力角。
暂时取8
7.求算b1、b2须先求算bmax、bmin。
依据铰销B、D的坐标,可建立它们之间距离的公式。
B的坐标为
XBasin()yBacos()
D的坐标为
XDe
yDhS
式中——曲柄转角,取升程起始时的=0°;
S——与相对应的从动杆位移,即铰销D至其最低位置的距离。
S值分为升程(=0~1)、最高位置停留(=1~1+2)、降程(=1+2~1+2+3)、最
低位置停留(=1+2+3~360°)四个阶段求算。
b值为
b=(xBxD)2(yByD)2
(1)用matlab编程画出b与曲线图,并算出bmax、bmin:
clear
sm=100;
h=120;
e=0;
a=70;
d=8*pi/180;
fa1=110*pi/180;fa2=0*pi/180;
fa3=150*pi/180;fa4=100*pi/180;
fa01=0:
0.001:
fa1;
s=sm/2*(1-cos(pi*fa01/fa1));
xb=a*sin(d+fa01);yb=-a*cos(d+fa01);xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
plot(fa01,b);
max(b)
min(b)
holdon;
fa02=fa1;
s=sm;
xb=a*sin(d+fa02);yb=-a*cos(d+fa02);xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
plot(fa02,b,'r--d');
max(b)
min(b)
holdon;
fa03=fa1+fa2:
0.001:
fa1+fa2+fa3;
s=sm*(1-(fa03-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa03-fa1-fa2)/fa3));xb=a*sin(d+fa03);
yb=-a*cos(d+fa03);
xd=e;yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
plot(fa03,b,'g-');
max(b)min(b)holdon;
fa04=fa1+fa2+fa3:
0.001:
fa1+fa2+fa3+fa4;
s=0;
xb=a*sin(d+fa04);yb=-a*cos(d+fa04);xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);plot(fa04,b,'r-');
max(b)
min(b)
xlabel('fa');ylabel('b');
title('fa-b');
运行结果:
ans=
217.0095
ans=
189.3564
b=
197.0794
b=
197.0794
ans=
197.0794
ans=
94.1923
ans=
190.0000
ans=
136.7980
由以上结果可以看出
bmax217.0095
bmin94.1923
并且b取最大值时,fa=1.2~1.4;b取最小值时,fa=3.5~3.7
2)根据bmax、bmin计算b1、b2
1
b12(bmaxbmin)
1
b22(bmaxbmin)
bmax217.0095
bmin94.1923
解得:
b1=61.4086
b2=155.6009
8、设计凸轮廊线
固定凸轮的理论廊线就是滚子中心C的运动轨迹线,根据铰销B、D的位置及b1、b2
值可确定C的位置。
参阅1,令铰销B、D的连线BD与DOD1线(或y轴)的夹角为θ,BD与CD的夹角为β,则
xBXDxBxD
arcsinarctg
byDyB
arccosb2b22b12
arccos21
2bb2
显然,XB>XD时θ为正值,反之则为负值,而β始终为正值。
这样,铰销C的坐标为xcxDb2sin()
ycyDb2cos()
该式对直动和摆动两种从动杆类型都适用,运算符号“+”和“—”的确定原则是:
令
B=bmax时的为m,b=b时的为′m,则对于AB推动BC的驱动方案(如图4所示),
在=m~′m区间,取“—”号;在=0~m和=′m~360°区间,取“+”
对于AB拉动BC的驱动方案,则刚好相反。
(1)用matlab求famax、famin
clear
sm=100;
h=120;
e=0;
a=70;
d=8*pi/180;
fa1=110*pi/180;fa2=0*pi/180;
fa3=150*pi/180;
fa4=100*pi/180;
fa01=1.2:
0.01:
1.4;
s=sm/2*(1-cos(pi*fa01/fa1));
xb=a*sin(d+fa01);
yb=-a*cos(d+fa01);
xd=e;
yd=h+s;
b1=sqrt((xb-xd).^2+(yb-yd).^2);
f=polyval(b1,fa01);
fa03=3.5:
0.01:
3.7;
s=sm*(1-(fa03-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa03-fa1-fa2)/fa3));xb=a*sin(d+fa03);
yb=-a*cos(d+fa03);
xd=e;
yd=h+s;
b3=sqrt((xb-xd).^2+(yb-yd).^2);
f=polyval(b3,fa03);
运行结果:
>>b1
b1=
Columns1through13
216.1970216.3140216.4223216.5220216.6128216.6945216.7672216.8306
216.8846216.9291216.9639216.9890217.0042
Columns14through21
217.0095217.0046216.9896216.9642216.9284216.8821216.8252216.7575>>fa01fa01=
Columns1through13
Columns14through21
>>b3b3=
Columns1through13
94.193694.207094.234794.276694.3325
Columns14through21
>>fa03fa03=
Columns1through13
3.5000
3.5100
3.5200
3.5300
3.5400
3.5500
3.5600
3.5700
3.58003.59003.60003.61003.6200
3.7000
Columns14through213.63003.64003.65003.66003.67003.68003.6900
由以上数据可以看出:
famax=1.33famin=3.58
(2)凸轮的设计
clear
sm=100;
h=120;
e=0;
a=70;d=8*pi/180;
fa1=110*pi/180;fa2=0*pi/180;
fa3=150*pi/180;
fa4=100*pi/180;
famax=1.33;famin=3.58;
b1=61.4086;b2=155.6009;
fa01=0:
0.002:
famax;s=sm/2*(1-cos(pi*fa01/fa1));
xb=a*sin(d+fa01);yb=-a*cos(d+fa01);
xd=e;
yd=h+s;b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
xc=xd+b2*sin(theta1+beta1);yc=yd-b2*cos(theta1+beta1);
plot(xc,yc);
holdon;
fa02=famax:
0.002:
fa1;s=sm/2*(1-cos(pi*fa02/fa1));
xb=a*sin(d+fa02);yb=-a*cos(d+fa02);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
xc=xd+b2*sin(theta1-beta1);
yc=yd-b2*cos(theta1-beta1);
plot(xc,yc,'r');
holdon;
fa03=fa1+fa2:
0.002:
famin;
s=sm*(1-(fa03-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa03-fa1-fa2)/fa3));xb=a*sin(d+fa03);
yb=-a*cos(d+fa03);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
xc=xd+b2*sin(theta1-beta1);
yc=yd-b2*cos(theta1-beta1);
plot(xc,yc);
holdon;
fa04=famin:
0.002:
fa1+fa2+fa3;
s=sm*(1-(fa04-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa04-fa1-fa2)/fa3));xb=a*sin(d+fa04);
yb=-a*cos(d+fa04);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);
beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
xc=xd+b2*sin(theta1+beta1);
yc=yd-b2*cos(theta1+beta1);
plot(xc,yc,'r');
holdon;
fa05=fa1+fa2+fa3:
0.002:
fa1+fa2+fa3+fa4;
s=0;
xb=a*sin(d+fa05);
yb=-a*cos(d+fa05);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);
beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
xc=xd+b2*sin(theta1+beta1);yc=yd-b2*cos(theta1+beta1);plot(xc,yc);
title('凸轮轮廓曲线');
9.检验压力角
(1)凸轮的压力角1
),BC重合,
、vc的斜率,
参阅图1,1为PC和Vc的夹角。
PC为驱动铰销运动的力(不考虑摩擦力vc为铰链C的运动方向,,与C点的凸轮廊线切线重合。
用K1、K2分别表示则
K1=ycyB
xcxB
K2K1
a1arctg
11K1K2
应保证a1的最大值不超过许用值,即a1m(a1)。
可取(a1)45oclear
sm=100;
h=120;
e=0;
a=70;
d=8*pi/180;
fa1=110*pi/180;fa2=0*pi/180;
fa3=150*pi/180;
fa4=100*pi/180;
b1=61.4086;
b2=155.6009;famax=1.33;
famin=3.58;
fa01=0:
0.001:
famax;s=sm/2*(1-cos(pi*fa01/fa1));
xb=a*sin(d+fa01);yb=-a*cos(d+fa01);
xd=e;yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));xc=xd+b2*sin(theta1+beta1);yc=yd-b2*cos(theta1+beta1);
k11=(yc-yb)./(xc-xb);
fori=2:
length(fa01)-1k21(i)=(yc(i-1)-yc(i+1))./(xc(i-1)-xc(i+1));
endk21
(1)=k21
(2);
fori=2:
length(fa01)-1
a1(i)=abs(atan((k21(i)-k11(i))./(1+k11(i)*k21(i))))*180/pi;end
a1
(1)=a1
(2);
dfa01=fa01(2:
length(fa01));plot(dfa01,a1);
holdon;
fa02=famax:
0.002:
fa1;s=sm/2*(1-cos(pi*fa02/fa1));
xb=a*sin(d+fa02);
yb=-a*cos(d+fa02);
xd=e;yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));xc=xd+b2*sin(theta1-beta1);yc=yd-b2*cos(theta1-beta1);
k11=(yc-yb)./(xc-xb);
fori=2:
length(fa02)-1k21(i)=(yc(i-1)-yc(i+1))./(xc(i-1)-xc(i+1));
end
k21
(1)=k21
(2);
fori=2:
length(fa02)-1
a2(i)=abs(atan((k21(i)-k11(i))./(1+k11(i)*k21(i))))*180/pi;end
a2
(1)=a2
(2);
dfa02=fa02(2:
length(fa02));
plot(dfa02,a2);
holdon;
fa03=fa1+fa2:
0.002:
famin;
s=sm*(1-(fa03-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa03-fa1-fa2)/fa3));xb=a*sin(d+fa03);
yb=-a*cos(d+fa03);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));xc=xd+b2*sin(theta1-beta1);
yc=yd-b2*cos(theta1-beta1);
k11=(yc-yb)./(xc-xb);
fori=2:
length(fa03)-1k21(i)=(yc(i-1)-yc(i+1))./(xc(i-1)-xc(i+1));
end
k21
(1)=k21
(2);
fori=2:
length(fa03)-1
a3(i)=abs(atan((k21(i)-k11(i))./(1+k11(i)*k21(i))))*180/pi;end
a3
(1)=a3
(2);dfa03=fa03(2:
length(fa03));
plot(dfa03,a3);
holdon;
fa04=famin:
0.002:
fa1+fa2+fa3;
s=sm*(1-(fa04-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa04-fa1-fa2)/fa3));xb=a*sin(d+fa04);
yb=-a*cos(d+fa04);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));xc=xd+b2*sin(theta1+beta1);yc=yd-b2*cos(theta1+beta1);
k11=(yc-yb)./(xc-xb);
fori=2:
length(fa04)-1k21(i)=(yc(i-1)-yc(i+1))./(xc(i-1)-xc(i+1));
endk21
(1)=k21
(2);
fori=2:
length(fa04)-1a4(i)=abs(atan((k21(i)-k11(i))./(1+k11(i)*k21(i))))*180/pi;
enda4
(1)=a4
(2);dfa04=fa04(2:
length(fa04));
plot(dfa04,a4);
holdon;
fa05=fa1+fa2+fa3:
0.002:
fa1+fa2+fa3+fa4;
s=0;
xb=a*sin(d+fa05);yb=-a*cos(d+fa05);
xd=e;yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));xc=xd+b2*sin(theta1+beta1);yc=yd-b2*cos(theta1+beta1);
k11=(yc-yb)./(xc-xb);
fori=2:
length(fa05)-1k21(i)=(yc(i-1)-yc(i+1))./(xc(i-1)-xc(i+1));
endk21
(1)=k21
(2);
fori=2:
length(fa05)-1
a5(i)=abs(atan((k21(i)-k11(i))./(1+k11(i)*k21(i))))*180/pi;end
a5
(1)=a5
(2);dfa05=fa05(2:
length(fa05));
plot(dfa05,a5);
holdon;
xlabel('fa');ylabel('a');
title('凸轮压力角');
由上图可知a145,满足许用值。
(2)从动杆的压力角a2
a2为CD杆对铰销D的驱动力(不考虑摩擦力)与D的运动方向的夹角。
对于直动从动杆,显然
对于AB推动BC的驱动方案,在m~m区间取“—”号,其它区间取“+”号;而对于AB拉动BC的驱动方案,刚好相反。
clear
sm=100;
h=120;
e=0;
a=70;d=8*pi/180;
fa1=110*pi/180;fa2=0*pi/180;
fa3=150*pi/180;
fa4=100*pi/180;b1=61.4086;
b2=155.6009;
famax=1.33;
famin=3.58;
fa01=0:
0.001:
famax;
s=sm/2*(1-cos(pi*fa01/fa1));
xb=a*sin(d+fa01);
yb=-a*cos(d+fa01);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
afa=abs(theta1+beta1);plot(fa01,afa);
holdon;
fa02=famax:
0.002:
fa1;
s=sm/2*(1-cos(pi*fa02/fa1));
xb=a*sin(d+fa02);
yb=-a*cos(d+fa02);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
afa=abs(theta1-beta1);
plot(fa02,afa);
holdon;
fa03=fa1+fa2:
0.002:
famin;
s=sm*(1-(fa03-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa03-fa1-fa2)/fa3));xb=a*sin(d+fa03);
yb=-a*cos(d+fa03);
xd=e;
yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);
theta1=asin((xb-xd)./b);beta1=acos((b.^2+b2.^2-b1.^2)./(2*b*b2));
afa=abs(theta1-beta1);
plot(fa03,afa);
holdon;
fa04=famin:
0.002:
fa1+fa2+fa3;
s=sm*(1-(fa04-fa1-fa2)/fa3+1/(2*pi)*sin(2*pi*(fa04-fa1-fa2)/fa3));xb=a*sin(d+fa04);yb=-a*cos(d+fa04);xd=e;yd=h+s;
b=sqrt((xb-xd).^2+(yb-yd).^2);theta1=asin((x