死区时间的影响与形成.docx

死区时间的影响与形成.docx

《死区时间的影响与形成.docx》由会员分享，可在线阅读，更多相关《死区时间的影响与形成.docx（14页珍藏版）》请在冰豆网上搜索。

死区时间的影响与形成

死区时间参数

摘要：

针对不同厂家IPM要求的死区时间参数的不同，本文从硬件电路角度出发，提出一种延时电路方案，解决了因参数调整而引起软件的不统一问题，进而为MCU的大批量mask降低成本提供可能。

   关键词：

IPM   死区时间 

   随着现代电力电子技术的飞速发展，以绝缘栅双晶体管（IGBT）为代表的功率器件在越来越多的场合得到广泛地应用。

IGBT是VDMOS与双极晶体管的组合器件，集MOSFET与GTR的优点于一身，既具有输入阻抗高，开关速度快，热稳定性好和驱动电路简单的长处，又具有通态电压低，耐压高和承受大电流的优点，特别适合于电机控制。

现代逐渐得到普遍推广的变频空调，其内部的压缩机控制单元就是采用以IGBT为主要功率器件的新型智能模块（IPM）。

   IPM（智能功率模块）即IntelligentPowerModule的缩写，它是将输出功率器件IGBT和驱动电路、多种保护电路集成在同一模块内，与普通IGBT相比，在系统性能和可靠性上均有进一步提高，而且由于IPM通态损耗和开关损耗都比较低，使散热器的尺寸减小，故整个系统的尺寸减小。

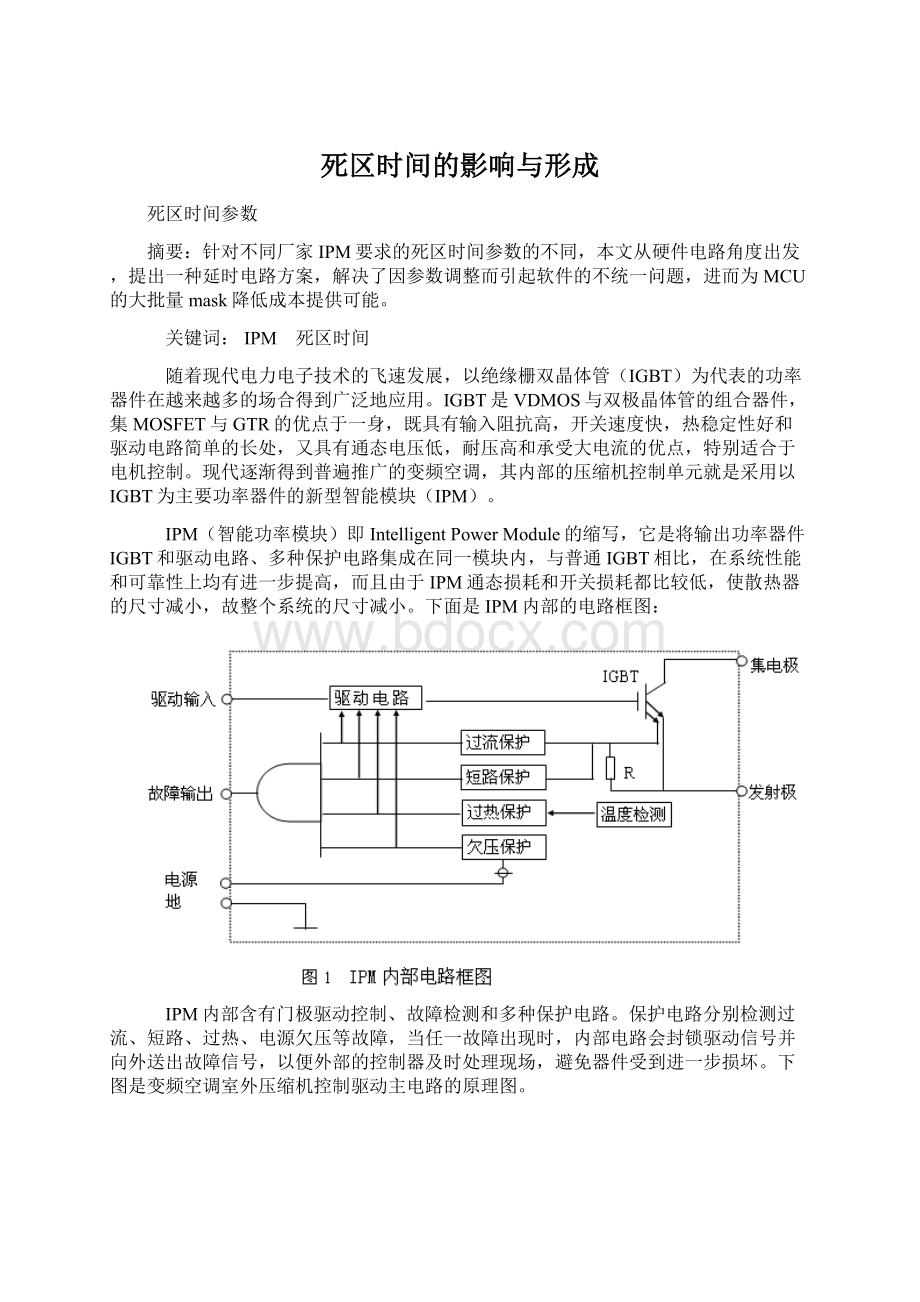
下面是IPM内部的电路框图：

   IPM内部含有门极驱动控制、故障检测和多种保护电路。

保护电路分别检测过流、短路、过热、电源欠压等故障，当任一故障出现时，内部电路会封锁驱动信号并向外送出故障信号，以便外部的控制器及时处理现场，避免器件受到进一步损坏。

下图是变频空调室外压缩机控制驱动主电路的原理图。

   220V交流电压经过由D1～D4和电解电容C1组成的桥式整流和阻容滤波电路后成为给IPM供电的直流电压，六个开关管按照一定规律通断，分别在U、V、W三相输出一系列的矩形信号，通过调整矩形波的频率与占空比达到调节输出电压频率和幅度的目的，即现在应用最广泛的PWM（PULSEWIDTHMODULATE脉冲宽度调制）控制技术，PWM控制技术从控制思想上可以分成四类：

等脉宽PWM法、正弦波PWM法、磁链追踪PWM法和电流追踪型PWM法。

不管采用何种控制方式，都必须注意U、V、W任意一相上下两个桥臂不能同时导通，否则直流电源将在IPM内部形成短路，这是绝对不允许的。

为了避免电源元件的切换反应不及时可能造成的短路，一定要在控制信号之间设定互锁时间，这个时间又叫换流时间，或者叫死区时间。

   死区时间，一般情况下软件工程师在程序设计时就会考虑并写进控制软件。

但是，由于不同公司生产的IPM，对死区时间长短的要求不尽相同，这样软件就会出现多个版本，不便于管理，并且影响CPU的MASK（掩模）工作。

为了控制软件的统一性，有的软件工程师将死区时间放到芯片外扩展的E2中，对不同公司的IPM，只需改变一下E2中的数据，即可简单实现死区时间的匹配。

这种方法的缺点是生产成本较高，在实际应用时受到一定限制。

随着集成电路工艺的不断改进，各种逻辑门集成电路的价格不断地下降，使采用硬件电路实现死区时间设定应用到生产上成为可能，这种方法的优点是电路简单，延时时间方便可调，成本低廉。

   方案原理图如下图3：

   控制过程如下：

因为IPM控制输入低电平有效。

平时CPU输出控制脚1处于高电平，逻辑或门输出高电平，IPM输入锁定。

当CPU输出低电平有效时，高频瓷片电容通过电阻放电，逻辑或门输入脚2仍然维持高电平，逻辑或门输出高电平，IPM输入仍然锁定。

当电容放电完毕，或门输入脚2变为低电平时逻辑输出才为低电平，IPM控制输入有效，因此，电容放电时间就是CPU控制输出到IPM控制输入有效的延时时间。

当CPU控制输出关断即输出重新变为高电平时，尽管电容处于充电状态而使或门输入脚2处于低电平，逻辑或门输出仍然立即变为高电平，锁定IPM输入。

上述电路只是六路IPM控制输入的其中一路，其他五路做同样处理，通过调整R、C的参数，就可以实现所需要的延时时间。

下面是一相电路控制时序图：

下面我们推导图3所示电路中电阻和电容的选择：

   根据电工学公式，由电阻、电容组成的一阶线性串联电路，电容电压Uc可以用下式表示：

   Uc=Uoexp（-t/τ）                    

（1）

τ为时间常数   τ=RC

在图3所示电路中，我们选择ST公司生产的高速CMOS或门电路，它的关门电平为1.35V（电源电压为4.5V），即当输入电压降至1.35/4.5U0=0.3U0时，输出电平转换有效，因此由式

（1）可以推导出：

td=-τln0.3=1.2RC                     

（2）

   上式就是我们选择R、C值的指导公式。

   例如：

需要延时时间为10us，选择精度为5%高频瓷片电容，容量为103P，则

   R=10*10e-6/1.2C=833Ω，这样R就可选择精度为1%、阻值为820Ω的金属膜电阻。

   小结：

按照上述方案设计的硬件延时电路，结构简单，成本低廉，可靠性极高，在实际使用时只需简单调换一下电阻的阻值就可实现对死区时间要求不同的IPM的控制。

对于一个反馈控制器而言，如何处理生产过程调节中的死区时间是个棘手的问题，此处我们将讨论几种处理方案。

Smith预估器使得控制器不再依靠测量到的过程变量，而是依靠改进后的过程变量反馈值（该预估值仅包含系统扰动，而不包含

死区时间）来进行调节作用。

如果以上方法运用得当，并且所运用的过程数学模型确实与实际生产过程相匹配，那么在系统设定值改变或生产负荷对生产过程形成干扰时，控制器就可推导出相对于系统某个设定值的实际过程值。

　　无奈的是，以上条件仅仅是假设。

对于控制器而言，在没有死区时间的情况下来满足以上控制目标当然不难，难的是如何得到实现以上控制方案所需的过程数学模型。

即使过程数学模型与实际生产过程之间存在一点点很小的“不匹配”，也会使得控制器无法成功的算出改进后的、准确的过程反馈值，相反，系统将推导出一个“谬之千里”的过程实际值。

　　有人提议可以用多种方法来改进基本Smith预估器的使用效果，就如对于死区时间的处理也具有多种可以互为替换的方案一样，然而尽管如此，死区时间的处理仍然是控制过程中非常棘手的问题。

对于一个反馈控制系统，死区时间可以定义为从“测量传感器检测到变量开始改变的瞬时”到“控制器对生产过程开始施加正确有效干预的瞬时”之间的延迟时间。

在死区时间内，生产过程的实际值根本不会对控制器的调节作用起任何反应。

在系统反应的死区时间结束之前，任何试图操纵或改变过程实际值的努力都注定是徒劳的。

　　举个例子，我们不妨想象一下“驾驶一辆方向盘很松的小汽车的过程”。

小车司机如想拐弯，他一定要使劲打方向盘才能克服方向盘太松而带来的滞差，并真正施加作用在操纵杆上。

只有在此之后，小车司机才能感觉到汽车方向的改变。

所有完成这一系列动作的时间就是死区时间。

　　死区时间问题是有据可查的最难克服的控制类问题之一。

在上面的例子中，如果一个司机对汽车拐弯过程中的死区时间大小估计不对的话，可能会因为上次的拐弯动作效果不佳，而在本次的拐弯过程中动作过于剧烈。

图1：

如果光学测厚仪安装得离轧辊太远，那么控制器要花

较长的时间才能够纠正钢板的厚度偏差。

这时还可能

由于调节过于“冒进”而使情况变得更糟。

然而，如果司机发现“在原来估算的死区时间结束之前汽车就已经开始拐弯”之后再采取缓解措施就为时已晚了，因为此前的操作动作早已矫枉过正，而且本应早些结束的。

在此之后，司机又不得不试图再拐回原有方向，这样可能最终引发拐弯过程的失控。

顺便提及一下，类似的原因也是如此众多的酒后驾驶事故的罪魁祸首。

也许汽车的方向盘拐弯是灵敏的，但是一个醉酒的司机由于感官不灵，等到他觉察到汽车开始拐弯时汽车就已经拐向过头了。

在这种情况下，拐弯过程的失控是由人的感官迟钝导致，而非设备调节过程的死区时间，然而这种情况导致的结果却是灾难性的。

传感器的安装位置，控制器的偏差容错度

在上述两种情况中，显而易见，消除死区时间是解决该控制难题的最佳途径。

汽车的方向盘应该加紧，司机任何时候都应该保持清醒状态。

然而，死区时间有时无法被完全消除。

我们不妨以热轧钢机为例，它有一对相向的轧辊，用于将热钢材轧成规格一致的薄钢板（见图1）。

在轧辊的下游位置有一测厚仪，用来测量刚轧好的薄钢板厚度，控制器再依据此反馈信号来增减轧辊作用于钢材上的压力，并以此方法来保证钢板厚度不会超出规格范围。

按照理想状况，测厚仪的安装位置应该尽量靠近轧辊，因为这样可将“轧辊的压力变化”与“由此引起的厚度变化”之间的死区时间置于最小。

否则，如安装位置太远，控制器就可能无法及时识别偏差，而如果我们将此识别过程设置得足够快，就可避免钢板的厚度不均问题。

更糟的是如果死区时间的影响较为可观，还会导致控制器的调节作用过于剧烈。

正如那位驾驶具有反应滞后方向盘的汽车司机一样，控制器也会以为其先前的调节作用没有效果而将控制作用加得更强。

事实上，在钢板的厚度变化最终体现出来之前，由于控制器的累计效应，使得其输出值与初始值之间的偏差早已大大的超调了，因此又会导致相反方向上的偏差。

此种调节过程，会使得轧辊施加在钢材上的压力持续的上下波动，大量钢板会由此产生侧向皱褶，并最终导致报废。

最为无奈的是，由于测厚仪无法在紧挨着轧辊接触钢材的位置进行安装，因此刚刚轧好的钢板必须要向下游移动一段距离后，才能够测量到厚度，这样的话，调节过程存在一些死区时间也就在所难免了。

这种我们称之为“传输延时”的现象，影响到很多“牵涉到物料需要从执行器到传感器之间传输”的生产流程，如流经管线的流体，吹过风管的空调风，顺着传输带移动的物体等等。

在以上任何一种情况下，如果将传感器的安装位置尽可能的靠近执行器，就可以最大限度的减少死区时间。

然而，死区时间的完全消除是难以做到的。

PID参数的整定

要处理自控系统中无法避免的死区时间问题，另外一种方案就是赋予控制器一定限度的“耐性”，或称之为“偏差容错度”。

实施这一方案最为简单有效的办法就是：

减弱控制器的整定参数，并以此来减缓系统的响应速度。

图2：

Smith预估器使用了一个过程对象的模型（包括增益，时间常数以及死

区时间）来预估在“没有其它干扰及死区时间”情况下的过程实际值。

对于一个PID（比例－积分－微分）回路，控制器整定参数的减弱往往意味着限制控制器的积分作用。

毕竟积分器的作用是“只要设定值和过程实际值之间存在偏差，就要持续不断的、以一定的比率来增加或减少控制器的输出值”。

然而对于存在死区时间的场合，由于控制器需要经过较长时间才能开始以正确的调节作用来纠正偏差，因此偏差往往很长时间都会存在，以致积分器一直都在进行积分作用，最终导致系统超调。

解决方法就是让积分器适时停止积分作用，以避免超时积分引发的系统超调。

JohnG.Ziegler和NathanielB.Nichols在他们1942年发表的关于PID回路整定的著名论文中曾经指出：

减弱PID控制器的调节作用的最佳方法是以1/d2的计算因子来减少积分整定常数,此处d等于调节过程的死区时间。

他们同时指出：

比例整定常数应该以1/d的计算因子来减少。

对于微分整定常数这一项，他们并未推荐能够减弱控制器调节作用的方法。

PID参数因子的警示

本文中提到的比例、积分、微分整定常数，实际上就是在PID控制规则中以理论方式表现出的P、I以及D参数：

此处CO（t）是以时间t为自变量的控制器输出，而e（t）是过程变量实际值与设定值之间的偏差。

Ziegler和Nichols所用到的PID控制规则以及事实上所有的现代PID控制器，它们都会采取不同整定常数的不同形式。

“以1/d2或1/d为因子来减弱PID控制器的整定参数”并非适用于本文示例之外的所有PID控制器。

对于每个可用于替换的PID算式，也能使用其它的因子来减弱整定参数，并且能够