工程力学4.docx
《工程力学4.docx》由会员分享,可在线阅读,更多相关《工程力学4.docx(18页珍藏版)》请在冰豆网上搜索。
工程力学4
三、主观题(共15道小题)
15.
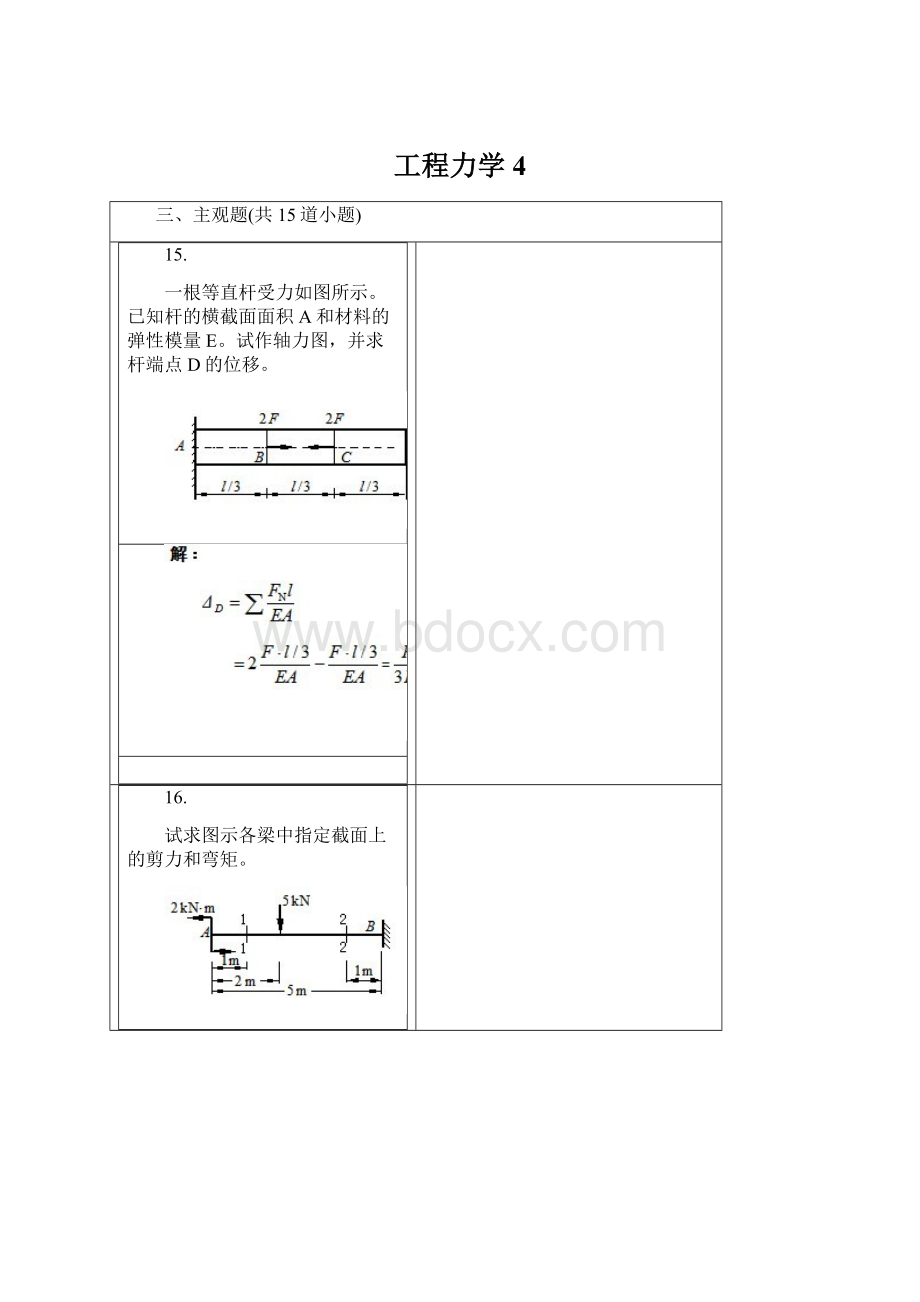
一根等直杆受力如图所示。
已知杆的横截面面积A和材料的弹性模量E。
试作轴力图,并求杆端点D的位移。
16.
试求图示各梁中指定截面上的剪力和弯矩。
17.
试指出图示剪力图和弯矩图的错误。
18.
矩形截面的悬臂梁受集中力和集中力偶作用,如图所示。
试求截面m-m和固定端截面n-n上A,B,C,D四点处的正应力。
19.
由两根28a号槽钢组成的简支梁受三个集中力作用,如图所示。
已知该梁材料为
Q235钢,其许用弯曲正应力
。
试求梁的许可荷载F。
20.
21.
22.
试求图a所示外伸梁指定横截面1-1、2-2、3-3、4-4上的剪力和弯矩。
23.
图a所示为一受满布均布荷载的悬臂梁。
试作此梁的剪力图和弯矩图。
解:
取x轴与梁的轴线重合,坐标原点取在梁的左端(图a)。
以坐标x表示横截面的位置。
然后,求任意x处横截面上的剪力和弯矩,也就是找出横截面上剪力和弯矩与横截面位置的函数关系,我们分别把这种函数关系式叫做梁的剪力方程和弯矩方程。
为此,将梁在任意x处用横截面截开。
显然,就此梁而言,若取左段分离体为研究对象(图b)则不必求支座约束力。
根据左段分离体的平衡条件便可列出剪力方程和弯矩方程如下:
以上两式后面括号里的不等式是用来说明对应的内力方程所适用的区段。
有了剪力方程和弯矩方程,便可在相应的坐标系里作出梁的剪力图(图c)和弯矩图(图d)。
此梁的剪力方程FS(x)=-qx表明FS(x)为x的线性函数,所以剪力图为一倾斜直线。
该直线可根据例如FS(0)=0与FS(l)=-ql作出。
(注:
剪力方程在x=l处是不适用的,因该处有集中支座约束力。
此处取x为l,实际上是指l稍左一点的截面)。
作弯矩图时,表示弯矩M的纵坐标(图d)取向下为正,以使梁的弯矩图始终位于梁的受拉一侧。
该梁的弯矩方程M(x)=-qx2/2表明M(x)是x的二次函数,弯矩图为二次抛物线。
在描点作图时至少需确定图线上的三个点,
例如,M(0)=0,M(l/2)=-ql2,M(l)=-ql2。
从内力图得知,固定端左侧横截面上的剪力和弯矩都有最大值,FS,max=ql,Mmax=ql2(内力的最大值一般都以绝对值为准)。
24.
对于图a所示受满布均布荷载的简支梁,试作剪力图和弯矩图。
25.
图a所示为一受集中荷载作用的简支梁。
试作其剪力图和弯矩图。
26.
试求图示诸梁中各指定的横截面上(1-1、2-2等)的剪力和弯矩。
(a)FS1=FS2=FS3=2kN,M1=-3kN·m,M2=-1kN·m,M3=-4kN·m
(b)FS1=0,FS2=FS3=-qa,FS4=-qa,
M1=0,M2=M3=-qa2,M4=-qa2
(c)FS1=ql,FS2=FS3=0,M1=M2=M3=ql2
(d)FS1=FS2=FS3=,M1=,M2=,M3=-
(e)FS1=3kN,FS2=FS3=-kN,M1=M2=-kN·m,M3=-kN·m
(f)FS1=FS2=0,FS3=qa,FS4=qa,M1=M2=M3=qa2,M4=qa2
(g)FS1=FS2=FS3=-F,M1=M2=0,M3=-Fl
(h)FS1=-ql,FS2=-ql,FS3=ql,M1=-ql2,M2=M3=–ql2
27.
试求图示折杆中各指定的横截面(1-1、2-2等)上的内力。
(a)FN1=FN2=10kN,FN3=0,FS1=0,FS2=0,FS3=10kN
M1=-10kN·m,M2=-10kN·m,M3=-10kN·m;
(b)FS1=F,M1=-Fa,T1=0;FS2=F,M2=0,T2=-Fa,
FS3=F,M3=-Fl,T3=-Fa
28.
试写出图示各梁的剪力方程和弯矩方程,并作出剪力图和弯矩图。
指出最大剪力和最大弯矩的值以及它们各自所在的横截面。
(a)∣FS,max∣=4kN,∣Mmax∣=3kN·m
(b)∣FS,max∣=4kN,∣Mmax∣=3kN·m
(c)∣FS,max∣=qa,∣Mmax∣=qa2
(d)∣FS,max∣=56kN,∣Mmax∣=192kN·m
(e)∣FS,max∣=9kN,∣Mmax∣=12kN·m
(f)∣FS,max∣=15kN,∣Mmax∣=30kN·m
(g)∣FS,max∣=F,∣Mmax∣=Fa
29.
在作剪力图和弯矩图时,作用于图a所示简支梁上的满布匀布荷载是否可以用图b所示的合力来代替这两种情况下的剪力和弯矩图各有什么不同