常见地分数小数及百分数地互化常用平方数立方数及各种计算方法.docx
《常见地分数小数及百分数地互化常用平方数立方数及各种计算方法.docx》由会员分享,可在线阅读,更多相关《常见地分数小数及百分数地互化常用平方数立方数及各种计算方法.docx(12页珍藏版)》请在冰豆网上搜索。
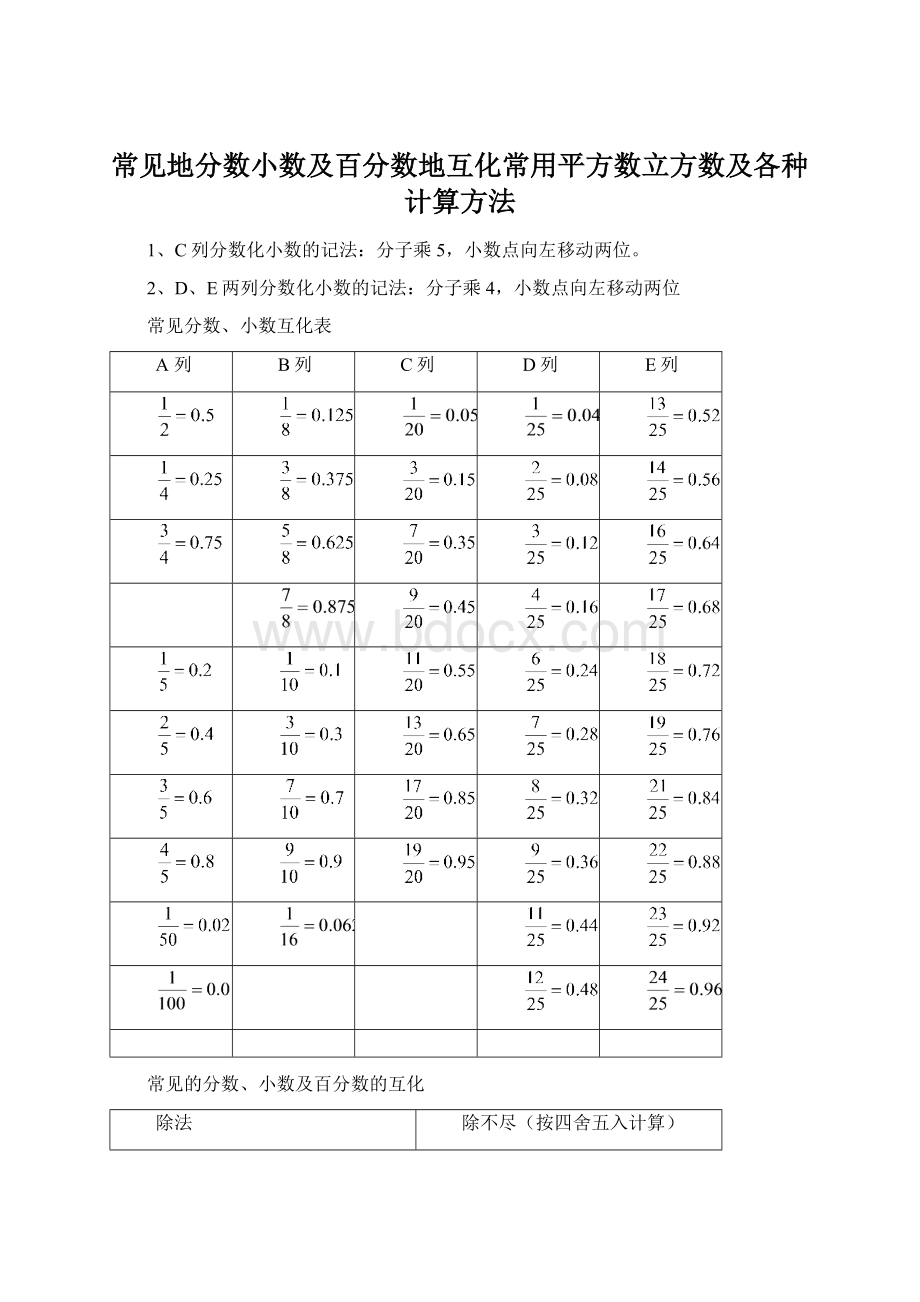
常见地分数小数及百分数地互化常用平方数立方数及各种计算方法
1、C列分数化小数的记法:
分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:
分子乘4,小数点向左移动两位
常见分数、小数互化表
A列
B列
C列
D列
E列
常见的分数、小数及百分数的互化
除法
除不尽(按四舍五入计算)
除法
比
分数
小数
百分
除法
比
分数
小数
百分
1÷2
1:
2
1/2
0.5
50%
1÷3
1:
3
1/3
0.33
33%
1÷4
1:
4
1/4
0.25
25%
2÷3
2:
3
2/3
0.67
67%
1÷5
1:
5
1/5
0.2
20%
1÷6
1:
6
1/6
0.17
17%
2÷5
2:
5
2/5
0.4
40%
5÷6
5:
6
5/6
0.83
83%
3÷5
3:
5
3/5
0.6
60%
1÷7
1:
7
1/7
0.14
14%
4÷5
4:
5
4/5
0.8
80%
2÷7
2:
7
2/7
0.29
29%
1÷8
1:
8
1/8
0.125
12.5%
3÷7
3:
7
3/7
0.43
43%
3÷8
3:
8
3/8
0.375
37.5%
4÷7
4:
7
4/7
0.57
57%
5÷8
5:
8
5/8
0.625
62.5%
5÷7
5:
7
5/7
0.71
71%
7÷8
7:
8
7/8
0.875
87.5%
6÷7
6:
7
6/7
0.86
86%
1÷10
1:
10
1/10
0.1
10%
1÷9
1:
9
1/9
0.11
11%
3÷10
3:
10
3/10
0.3
30%
2÷9
2:
9
2/9
0.22
22%
7÷10
7:
10
7/10
0.7
70%
4÷9
4:
9
4/9
0.44
44%
9÷10
9:
10
9/10
0.9
90%
5÷9
5:
9
5/9
0.56
56%
3÷2
3:
2
3/2
1.5
150%
7÷9
7:
9
7/9
0.78
78%
5÷4
5:
4
5/4
1.25
125%
8÷9
8:
9
8/9
0.89
89%
7÷5
7:
5
7/5
1.4
140%
4÷3
4:
3
4/3
1.33
133%
备注
除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无限循环)小数;除不尽与除尽相反,是无限循环小数。
常用平方数
11²=121
12²=144
13²=169
14²=196
15²=225
16²=256
17²=289
18²=324
19²=361
20²=400
21²=441
22²=484
23²=529
24²=576
25²=625
26²=676
27²=729
28²=784
29²=841
30²=900
31²=961
32²=1024
33²=1089
34²=1156
35²=1225
36²=1296
37²=1369
38²=1444
39²=1521
40²=1600
41²=1681
42²=1764
43²=1849
44²=1936
45²=2025
46²=2116
47²=2209
48²=2304
49²=2401
50²=2500
常见立方数
1³=1
2³=8
3³=27
4³=64
5³=125
6³=216
7³=343
8³=512
9³=729
常见特殊数的乘积
25×3=75
25×4=100
25×8=200
125×3=375
125×4=500
125×8=1000
625×16=10000
37×3=111
错位相加/减
A×9型速算技巧:
A×9=A×10-A;
例:
743×9=743×10-743=7430-743=6687
A×9.9型速算技巧:
A×9.9=A×10+A÷10;
例:
743×9.9=743×10-743÷10=7430-74.3=7355.7
A×11型速算技巧:
A×11=A×10+A;
例:
743×11=743×10+743=7430+743=8173
A×101型速算技巧:
A×101=A×100+A;
例:
743×101=743×100+743=75043
乘/除以5、25、125的速算技巧:
A×5型速算技巧:
A×5=10A÷2;
例:
8739.45×5=8739.45×10÷2=87394.5÷2=43697.25
A÷5型速算技巧:
A÷5=0.1A×2;
例:
36.843÷5=36.843×0.1×2=3.6843×2=7.3686
A×25型速算技巧:
A×25=100A÷4;
例:
7234×25=7234×100÷4=723400÷4=180850
A÷25型速算技巧:
A÷25=0.01A×4;
例:
3714÷25=3714×0.01×4=37.14×4=148.56
A×125型速算技巧:
A×5=1000A÷8;
例:
8736×125=8736×1000÷8=8736000÷8=1092000
A÷125型速算技巧:
A÷1255=0.001A×8;
例:
4115÷125=4115×0.001×8=4.115×8=32.92
减半相加:
A×1.5型速算技巧:
A×1.5=A+A÷2;
例:
3406×1.5=3406+3406÷2=3406+1703=5109
“首数相同尾数互补”型两数乘积速算技巧:
积的头=头×(头+1);积的尾=尾×尾
例:
23×27=首数均为2,尾数3与7的和是10,互补
所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621
本方法适合11~99所有平方的计算。
11X11=12121X21=414131X31=96141X41=1681
12X12=14822X22=48432X32=102442X42=176452X52=2704
从上面的计算我们可以得出公式:
个位=个位×个位所得数的个位,如果满几十就向前进几,
十位=个位×(十位上的数字×2)+进位所得数的末位,如果满几十就向前进几,
百位=两个十位上的数字相乘+进位。
例:
26×26=
个位=6×6=36,满30向前进3;
十位=6×(2×2)+3=27,满20向前=进2;
百位=2×2+2=6
由此可见26×26=676
23×23
个位=3×3=9
十位=3×(2×2)=12,写2进1
百位=2×2+进1=5
所以23×23=529
46×46个位=6×6=36,写6进3
十位=6×(4×2)+进3=51,写1进5
百位=4×4+进5=21,写1进2
所以46×46=2116
如果没有满十就不用进位,计算更简便。
例:
13×13
个位=3×3=9十位=3×(1×2)=6百位=1×1所以13×13=169
规律:
(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同。
(2)奇数的平方的个位数字是奇数,十位数字是偶数。
(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1。
(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
(6)完全平方数的形式必为下列两种之一:
3n,3n+1。
(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型。
(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9。
(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)
(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数。
(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数。
(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n)。
一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,
如0,1,8,27,64,125,216,343,512,729,1000等。
如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数。
x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数。
z和z²必定都是奇数。
五组常见的勾股数:
3²+4²=5²;5²+12²=13²;7²+24²=25²;8²+15²=17²;20²+21²=29²
9+16=25;25+144=169;49+576=625;64+225=289;400+441=841
记忆技巧:
(a+b)²=a²+b²+2ab(a-b)²=a²+b²-2ab
||||||
a×ab×b2×a×ba×ab×b2×a×b
例:
13²=(10+3)²=10²+3²+2×10×3=100+9+60=169
88²=(90-2)²=90²+2²-2×90×2=8100+4-360=7744
用处:
1训练计算能力,使计算更快更准确;
2估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到
之间的所有质数是不是n的因子即可,超过
的都不必检查了
例如:
判定2431是否为质数,因为49²=2401<2431<2500=50²,
所以49<
.<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=11×13×17
③增加对数字的熟悉程度,比如16²=256=28,32²=1024=210,64²=4096=212,另外一些特殊结构的数字应该牢记,如88²=7744,11²=121,22²=484,(121和484从左到右与从右到左看是一样的)12²=144,21²=441,13²=169,31²=961,(a左右颠倒后a²也左右颠倒)。
一、常用的π倍
1π
3.14
17π
53.38
92π
254.34
2π
6.28
18π
56.52
102π
314
3π
9.42
19π
59.66
112π
379.94
4π
12.56
20π
62.8
122π
452.16
5π
15.7
21π
65.94
132π
530.66
6π
18.84
22π
69.08
142π
615.44
7π
21.98
23π
72.22
152π
706.5
8π
25.12
24π
75.36
162π
803.84
9π
28.26
25π
78.5
172π
907.46
10π
31.4
26π
81.64
182π
1017.36
11π
34.54
27π
84.78
192π
1133.54
12π
37.68
28π
87.92
202π
1256
13π
40.82
29π
91.06
212π
1384.74
14π
43.96
30π
94.2
222π
1519.76
15π
47.1
62π
113.04
232π
1661.06
16π
50.24
72π
153.86
242π
1808.64
82π
200.96
252π
1962.5
小学单位换算
一、长度
(一)什么是长度?
长度是一维空间的度量。
(二)长度常用单位
*公里(km)*米(m)*分米(dm)*厘米(cm)*毫米(mm)*微米(um)
(三)单位之间的换算
1微米=1000纳米1毫米=1000微米1厘米=10毫米
1分米=10厘米1米=1000毫米1千米=1000米
1米=10分米=100厘米
二、面积
(一)什么是面积
面积,就是物体所占平面的大小。
对立体物体的表面的多少的测量一般称表面积。
(二)常用的面积单位
*平方毫米*平方厘米*平方分米*平方米*平方千米
(三)面积单位的换算
1平方厘米=100平方毫米1平方分米=100平方厘米1平方米=100平方分米
1公倾=10000平方米1平方公里=1平方千米=100公顷
1公顷=0.01平方千米≈15亩1平方千米=1000000平方米
1平方米=100平方分米=10000平方厘米
三、体积和容积
(一)什么是体积、容积
体积,就是物体所占空间的大小。
容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
(二)常用单位
1体积单位
*立方米*立方分米*立方厘米
2容积单位
*升*毫升
(三)单位换算
1体积单位
1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米
1立方米=1000立方分米1立方分米=1000立方厘米
2容积单位
1升=1立方米1升=1000毫升1毫升=1立方厘米
1立方米=1000升1立方分米=1升1立方厘米=1毫升
四、质量
(一)什么是质量
质量,就是表示表示物体有多重。
(二)常用单位
*吨t*千克kg*克g
(三)常用换算
1吨(t)=1000千克(kg)1千克=1000克(g)
重量单位换算
1吨=1000千克1千克=1000克1千克=1公斤
五、时间
(一)什么是时间
是指有起点和终点的一段时间
(二)常用单位
世纪、年、月、日、时、分、秒
(三)单位换算
*1世纪=100年1年=12月1年=365天平年一年=366天闰年.
一、三、五、七、八、十、十二是大月大月有31天
四、六、九、十一是小月小月有30天
平年2月有28天闰年2月有29天
1天=24小时1小时=60分1分=60秒1秒=1000毫秒(ms)1时=3600秒
货币
(一)什么是货币
货币是充当一切商品的等价物的特殊商品。
货币是价值的一般代表,可以购买任何别的商品。
(二)常用单位
*元*角*分
(三)单位换算
1元=10角1角=10分1元=100分
四则运算关系
加法:
一个加数=和-另一个加数
减法:
被减数=差+减数减数=被减数-差
乘法:
一个因数=积÷另一个因数
除法:
被除数=商×除数除数=被除数÷商
两个规律
1、除法的商不变规律:
被除数和除数同时乘或除以相同的数(0除外),商不变。
2、乘法的积不变规律:
如果一个因数乘几,另一个因数则除以几,那么它们的积不变。
数学简便运算方法归类
一、同级运算(没有括号),可以带着符号搬家
a+b+c=a+c+ba-b-c=a-c-ba+b-c=a-c+ba-b+c=a+c-b
a×b×c=a×c×ba÷b÷c=a÷c÷b
a×b÷c=a÷c×ba÷b×c=a×c÷b
二、有括号的同级运算,可以根据去括号的性质把括号去掉
1、括号前面是“+”号或“×”号,去掉括号不变号。
a+(b+c)=a+b+ca+(b-c)=a+b-ca×(b×c)=a×b×ca×(b÷c)=a×b÷c
2、括号前面是“-”号或“÷”号,去掉括号要变号。
a-(b+c)=a-b-ca-(b-c)=a-b+ca÷(b×c)=a÷b÷ca÷(b÷c)=a÷b×c
上面的式子从左到右可以去括号,那么从右到左就是添括号的方法了。
自己认真观察发现没有括号的同级运算中添括号的性质哦。
三、乘法分配律:
(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c
乘法分配律的逆运用:
a×c+a×b=(a+b)×c或a×c-b×c=(a-b)×c
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
1.分配法(从左到右的用法)括号里是加或减运算,与另一个数相乘,注意分配。
2.提取公因式(从右到左的用法)注意相同因数的提取。
3.注意构造,让算式满足乘法分配律的条件。
四、借来还去法
看到名字,就知道这个方法的含义。
用此方法时,需要注意观察,发现规律。
还要注意还哦,有借有还,再借不难嘛。
例:
9999+999+99+9
五、拆分法
顾名思义,拆分法就是为了方便计算把一个数拆成几个数。
这需要掌握一些“好朋友”,如:
2和5,4和5,2和2.5,4和2.5,8和1.25等。
分拆还要注意不要改变数的大小哦。
例:
3.2×12.5×251.25×883.6×0.25
以上几种方法包含了小学数学常见的简便运算的方法,在选择简便方法的时候一定要注意简便方法的依据,千万不能没有依据的胡拉乱扯一通,有时候是出题者故意挖的陷阱,看似可以运用简便算法,实际上找不出可以简便运算的依据,这样的题只能按照运算顺序计算的。
(例如2.5×4÷2.5×4,看似加括号很简便,结果等于1,而实际上括号加在除号的后面是要变号的,所以本道题的简便方法是“没有括号的同级运算,可以带着符号搬家。
2.5÷2.5×4×4)
简便计算简便运算重在找依据
1、运算定律:
运算定律用字母表示
加法交换律a+b=b+a
加法结合律(a+b)+c=a+(b+c)
乘法交换律a×b=b×a
乘法结合律(a×b)×c=a×(b×c)
乘法分配律(a+b)×c=a×c+b×c
减法运算规律a-b-c=a-(b+c)
除法运算规律a÷b÷c=a÷(b×c)
2、乘、除法的互化。
(小技巧:
符号是相反的;两个数相乘得“1”)
(1)A÷0.1=A×10(7)A÷0.01=A×100
(2)A×0.1=A÷10(8)A×0.01=A÷100
(3)A÷0.2=A×5(9)A÷0.25=A×4
(4)A×0.2=A÷5(10)A×0.25=A÷4
(5)A÷0.5=A×2(11)A÷0.125=A×8
(6)A×0.5=A÷2(12)A×0.125=A÷8
3、求近似数的方法。
(1)四舍五入法。
(2)进一法。
(3)去尾法
4、积与因数、商与被除数的大小比较:
第2个因数>1,积>第1个因数;除数>1,商<被除数;
第2个因数=1,积=第1个因数;除数=1,商=被除数;
第2个因数<1,积<第1个因数。
除数<1,商>被除数;