完整版一元二次方程综合培优含参考答案.docx
《完整版一元二次方程综合培优含参考答案.docx》由会员分享,可在线阅读,更多相关《完整版一元二次方程综合培优含参考答案.docx(34页珍藏版)》请在冰豆网上搜索。
完整版一元二次方程综合培优含参考答案
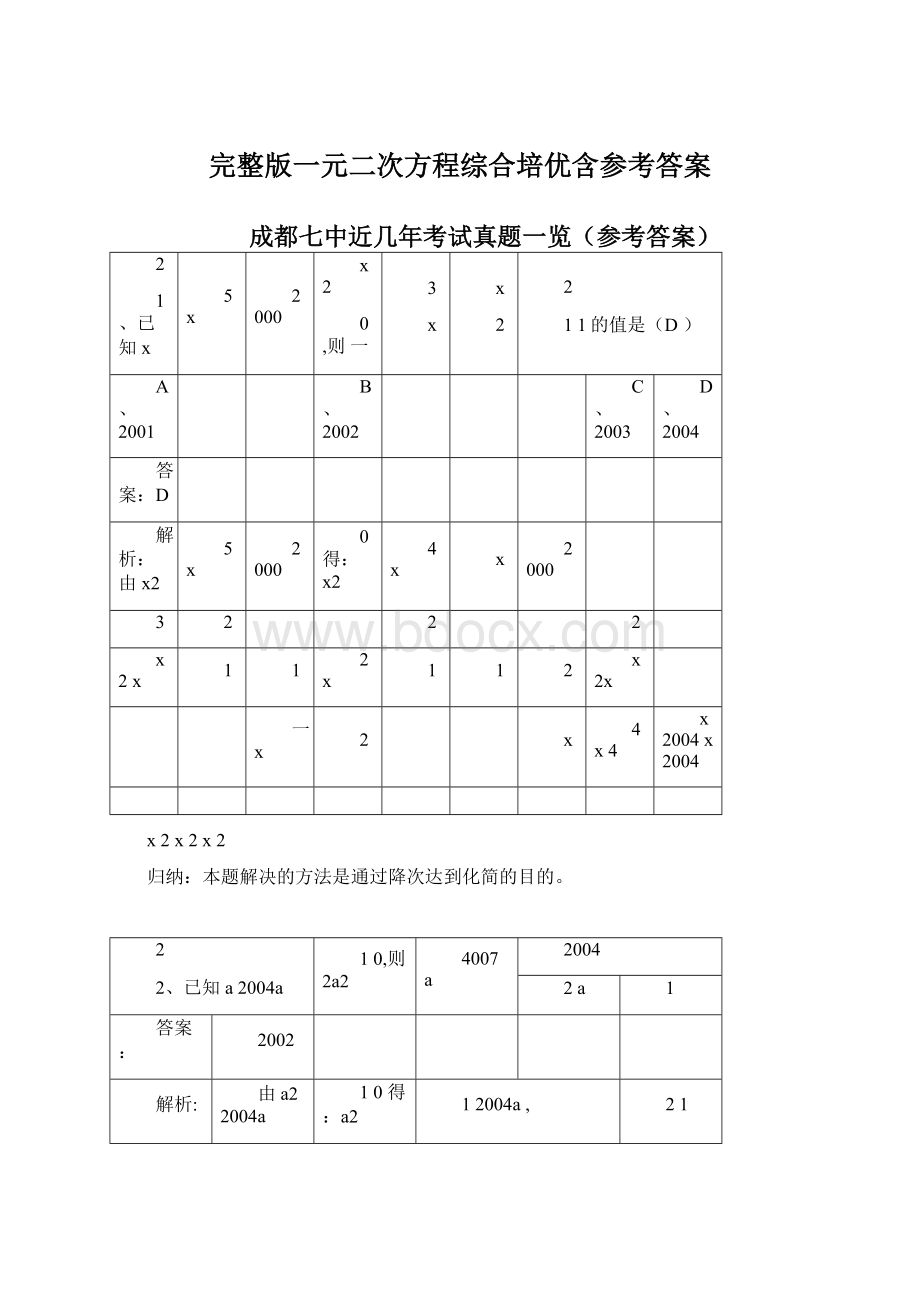
成都七中近几年考试真题一览(参考答案)
2
1、已知x
5x
2000
x2
0,则一
3
x
x
2
2
11的值是(D)
A、2001
B、2002
C、2003
D、2004
答案:
D
解析:
由x2
5x
2000
0得:
x2
4x
x
2000
3
2
2
2
x2x
1
1
2x
1
1
2
x2x
一x
2
x
4x4
x2004x2004
x2x2x2
归纳:
本题解决的方法是通过降次达到化简的目的。
2
2、已知a2004a
10,则2a2
4007a
2004
2a
1
答案:
2002
解析:
由a22004a
10得:
a2
12004a,
21
a2004a1,a2004
a
原式
22004a1
2004
4007a
a2
1
2002
气UUtci
2004a
a
归纳:
本题解决的方法是通过降次达到化简的目的。
22a
3、若ab1,且5a2005a70,7b2005b50,则卫
b
答案:
-
5
2
211
解析:
由7b2005b50得:
5-2005—70
bb
tab1,即a-
b
1
•••把a和1作为一元二次方程5x22005x70的两根
b
1a7
…a
bb5
归纳:
本题是通过构造一元二次方程的两根,利用根与系数的关系解决问题。
4、已知方程2x22ax3a40没有实数根,则代数式Va28a162a
答案:
2
考点:
根的判别式。
分析:
由方程2x2ax3a
4
0没有实数根,得
0,求的a的范围,然后根据此范围
化简代数式。
解答:
解:
•••已知方程2x2
2ax
3a40没有实数根
0,即4a2423a
4
2
0,a6a80,
得2a4
则代数式Va28a16|2a||a4||a2|4aa22
归纳:
本题考查了一元二次方程根的判别式。
当0时,方程没有实数根。
同时考查了
元二次不等式的解法、二次根式的性质和绝对值的意义。
5、已知y2x,6x,贝Uy的最大值为.
答案:
97
8
考点:
二次函数的最值。
专题:
计算题;换兀法.
分析:
此题只需先令6xt
0,用
x表示t,代入求
y关于t的二次函数的最值即可。
解答:
令..6xt0,x6
2t
则y
2x6x122t2t
2t2
1t122t
2
1
12-
48
1
又t0,且y关于t的二次函数开口向下,则在t-处取得最大值
4
即y最大值为伐1,即97
88
归纳:
本题考查了二次函数的最值,关键是采用换元法,将.6x用t来表示进行解题比较
简便。
6、已知abe
0,
abe2,
e
0,则(
)
A、ab0
B、a
b
2
C、ab
3D、ab4
答案:
B
考点:
根的判别式。
专题:
综合题。
分析:
由abe
0,
abe2,
e
0,得到a,
b两个负数,
2
再由abe,ab-,这
e
样可以把a,b看作方程x2ex-0的两根,根据根的判别式得到c24-0,解得c2,
e
e
然后由a
b
e得到ab
2.
解答:
abe0,
abe
2,
e
0
a
0,
b0,e0
二a
b
2e,ab
e
•可以把
a,b看作方程
2x
ex
2
e
0
2e
2
420,解得e
e
2
•e
a
b2,即a
b
2
点评:
本题考查了一元二次方程根的判别式:
如方程有两个实数根,则0•也考查了元二次方程根与系数的关系以及绝对值的含义。
2
7、已知ab8,abc160,贝Uabe
答案:
0
考点:
因式分解的应用;非负数的性质:
偶次方。
分析:
本题乍看下无法代数求值,也无法进行因式分解;但是将已知的两个式子进行适当变
形后,即可找到本题的突破口。
由ab8可得ab8;将其代入abc2160得:
b28bc2160;此时可发现b28b16正好符合完全平方公式,因此可用非负数的性质求
出b、c的值,
进而可求得
a的值;
然后代值运算即可。
解答:
•/
ab8
•ab
8
又tab
c2160
•-b28b
ic216
0,即b
22
4c20
二b4,c0
a4
abc0
归纳:
本题既考查了对因式分解方法的掌握,又考查了非负数的性质以及代数式求值的方法.
232
8、已知mm10,贝Um2m2006
答案:
2005
考点:
因式分解的应用。
专题:
整体思想。
分析:
根据已知条件可得到m2m1,然后整体代入代数式求值计算即可。
解答:
tm2m10
•2…m
m1
•原式
mm2mm2006m2
m200612006
2005
点评:
这里注意把要求的代数式进行局部因式分解,根据已知条件,整体代值计算。
2
9、已知ab4,abc40,则ab
答案:
0
考点:
拆项、添项、配方、待定系数法。
专题:
计算题.
分析:
先将字母b表示字母a,代入abc240,转化为非负数和的形式,根据非负数的性质求出a、b、c的值,从而得到ab的值。
解答:
tab4
•ab4
代入abc240,可得(b4bc240,即b22c20
•••ab42
二ab0
归纳:
本题既考查了对因式分解方法的掌握,又考查了非负数的性质以及代数式求值的方法。
解题关键是将代数式转化为非负数和的形式。
一2_
10、若方程xpxq0的二根为Xi,x2,且Xi1,pq30,则x2()
A、小于1B、等于1C、大于1D、不能确定
答案:
A
考点:
根与系数的关系.
专题:
计算题.
分析:
方程X2
pxq
0的二根为X1,X2,根据根与系数的关系及已知条件即可求解。
解答:
•••方程X2
px
q0的二根为X1,X2
•x1
X2P,
X1X2
q
•••X1
1,pq
3
•X1
X2X1x2
3
•X2
Xx23
X12
•X2
X12
•••x112
•x21
归纳:
本题考查了根与系数的关系,属于基础题,关键掌握x1,x2是方程x2pxq0的
两根时,x1x2p,x1x2
11、已知是方程X2X
q-
31
—一1的值为
1
4
0的一个根,则-
答案:
5
考点:
因式分解的应用。
专题:
整体思想。
分析:
根据已知条件可得到
2
1
-0,即
21
2-然后整体代入代数式求值计算即
4
4
可。
解答:
•/是方程
2
XX
1
0的一个根
4
•2
10,
即2
1
4
4
•原式
12
1
2
141
5
1
1
2
1
4
点评:
这里注意把要求的代数式进行局部因式分解,
根据已知条件,整体代值计算。
2432
12、若3xx1,则9x12x2x7x2008()
A、2011B、2010C、2009D、2008
答案:
B
考点:
因式分解的应用.
专题:
计算题;整体思想.
分析:
将3x2x1化简为3x2x10,整体代入9x412x32x27x2008变形的式
子3x23x2x15x3x2x123x2x12010,计算即可求解.
解答:
T3x2x1,即3x2x10
•••9x412x32x27x2008
2222
3x3xx15x3xx123xx12010
2010
归纳:
本题考查因式分解的运用,注意运用整体代入法求解。
13、方程3x23x22的解为.
答案:
2
3
考点:
利用方程的同解原理解答。
专题:
计算题。
解答:
3x23x22
两边同时平方得:
3x23x22.9x244
整理得:
..9x243x2
再平方得:
12x8
解得:
x-
3
归纳:
本题考查将无理方程通过平方的方式转化为有理方程解答。
22
14、已知2x6xy
22
0,则xy
2x的最大值疋(
)
A、14
B、15
C、16
D、18
答案:
B
考点:
完全平方公式。
分析:
由2x26xy2
0得y22x2
6x代入x2y2
2x,通过二次函数的最值,求出
它的最大值。
解答:
2x26xy20化为y22x26x,0y—,0x3
2
故x2y22x8xx2
二次函数开口向下,当x4时表达式取得最大值
由于0x3
所以x3时此时y0,表达式取得最大值:
15
点评:
本题是中档题,考查曲线与方程的关系,直接利用圆锥曲线解答比较麻烦,利用转化思想使本题的解答比较简洁,注意二次函数闭区间是的最大值的求法。
15、方程x22|x|2m恰有3个实根,则m()
答案:
专题:
换兀法。
分析:
设x2
3x
3
7y,原方程化成y空2,再整理成整式方程求解即可。
y
解答:
设x2
3x
7y,则y卫2
y
•2
…y
2y3
0,
解得y11,y23
当%
1时,
2
3V33
nv74布邳彳曰v
x
3x/1,解得x2
当y2
3时,
2x
3x73,解得x2或5
3
、33
3
、33
v0cah
2
2560
2
考点:
换元法解分式方程。
归纳:
本题考查了用换元法解分式方程,解次题的关键是把x23x7看成一个整体来计算,
即换元法思想。
17、关于x的一元二次方程2x25xa0(a为常数)的两根之比洛:
x?
2:
3,则x洛
A、1
B、2
答案:
C
考点:
一元一
.次方程根与系数的关系及求解。
解答:
设2x2
5x
a
0的两根分别为2k
2k
3k?
2k
3k
a
2
2
二k
1
a
3
3k,
c、
由根与系数的关系得:
D、
2
答案:
根与系数的关系;代数式求值;完全平方公式。
计算题。
归纳:
本题主要考查了方程的根的定义,一元二次方程根与系数的关系。
难度中等。
关键是
利用方程根的定义及完全平方公式将所求代数式降次,再结合根与系数的关系求解。
19、
若关于x的方程公亠
ax_1只有一解,求a的值。
x1xx
x
答案
:
a0或a—
2
考点
:
解分式方程。
分析
:
先将分式方程转化为整式方程,
把分式方程解的讨论转化为整式方程的解的讨论,
“只
有一个解”内涵丰富,在全面分析的基础上求出a的值。
解答:
原方程化为ax223ax10①
(1)当a0时,原方程有一个解,
(2)当a0时,方程①
22
5a4a10,总有两个不同的实数根,由题意知必有一个
根是原方程的增根,从原方程知增根只能是0或1,显然0不是①的根,故x1,得a-.
2
11
综上可知当a0时,原方程有一个解,x1,a-时,x2.
22
归纳:
本题考查了解分式方程。
注意:
分式方程转化为整式方程不一定是等价转化,有可能
产生增根,分式方程只有一个解,可能足转化后所得的整式方程只有一个解,也可能是转化后的
整式方程有两个解,而其中一个是原方
立,求fX
ax2bxca0的解析式。
2
考点:
函数恒成立问题;函数解析式的求解及常用方法;二次函数的性质。
专题:
综合题。
分析:
取x1,由1f111,能够求出f11的值;由f1
_a
0,知
b
c1
2
a
b
c0
所以ac
12
b,由xfx,对一切实数恒成立,知axbxcx,即
2
2
axb
1x
c0对
一切实数恒成立,由此能求出fx的表达式。
解答:
解:
(1)・.•二次函数fxax2bxca0满足f10且
xfx
2x
1
2
2x1
20、已知二次函数fxaxbxca0满足f10且xfx对一切实数恒成
•••取x1,得1
11
1
所以f11
•-acb-
2
•/xfx,对一切实数恒成立
•ax2b1xc0对一切实数恒成立
a0
…2
b14ac0
ac
16
1
ta0,ac一0
16
二c0
•••2ac2卫J,:
当且仅当ac4时,等式成立
•£1211
…fx—xx—
424
点评:
本题考查二次函数的性质的综合应用,考查函数解析式的求法,解题时要认真审题,仔细解答,注意函数恒成立条件的灵活运用。
2
21、已知fxaxbxca0.
(2)若fx
―2—在(人,X2)内有一根为m且人
x22m1.若fx
0的对
称轴为xx0.求证:
Xom2.
考点:
一元二次方程的根的分布与系数的关系;二次函数的性质;等差数列的性质.
专题:
计算题;转化思想.
分析:
(1)通过计算一元二次方程的判别式大于0,可得方程有两个不相等的实数根;设方
第9页共20页
程对应的函数为gx,由g石gX20,可得方程有一个根属于(石,x?
).
(2)由题意可得
rfX1fX2
即a2m2
2
X1
2
X2
b2mx
X20
由于
fm_
2
2
2
2
22
X1
x22m1,故b
222
a2mx1X2,
由X
b
2m
X1
X22
X1X2
证得结
0
m
2a
2
2
论。
解答:
证明:
(1)t
上fX1fX2
TX
2
2
•fxaxbxc
—axfbx1c
ax;
bx2c
2
整理得:
2ax22bx
22
ax1X2bx1
X2
0
故方程有两个不相等的实数根
fx1fx2
fXi
2
则gX1gX2
则gXgX2
故方程fx丄仝有一根在(X,X2)内。
2
(2)•••方程fx丄仝匕匚在(Xi,X2)内有一根为m
2
fXifX2
…fm-
2
a2m2xi2x;b2mxix20xix22m1
222
故Xo
b
2a
2
2m
22
XiX2
2
22
2XiX22
mm
2
…ba2mxx2
点评:
本题考查一元二次方程根的分布与系数的关系,二次函数的性质,等差数列的性质,体现了转化的数学思想。
•••把
和丄作为一元二次方程x2
3x10的两根
一元二次方程成都四中考试真题
1、若
1
x—
x
1,则x3
1
丄的值为(
x
)
A、3
B、4
C、5
答案:
4
考点:
因式分解的应用。
专题:
整体思想。
解答:
Tx
丄1
x
2
•3
1
12
1
1
1
…x
~3
X—X
12x
—
x34
x
x
x
x
x
归纳:
本题关键是将x
1
1作为整体,
31
然后将x3
进行因式分解变形解答。
x
x
2、已知实数、满足
2
310,
2310,
且
1,则23
的值为()
A、1
B、3
C、一3
D、10
答案:
D
解析:
由231
0得
:
13-
2
1
-0,即
1
2
131
1—,—
3
1,即
丄3,-1,即
1910
归纳:
本题是通过构造一元二次方程的两根,利用根与系数的关系解决问题。
3、实数x、y满足方程x2
2y2
2xyx3y10
,则y最大值为(
)
1
r3
3
A、-
B、一
C、
—
D、不存在
2
2
4
答案:
B
考点:
根的判别式。
专题:
计算题;转化思想。
分析:
先把方程变形为关于
x的
兀二次方程x2
12yx2y23y
10,由于此方程
有解,所以
0,这样得到y
的不等式
4y28y30,
解此不等式,得到
y的取值范围,
然后
找到最大值。
解答:
把x22y22xy
x3y
10看作为关于:
2
x的x12yx
2y23y1
0,并
22
4、方程2xx2的正根的个数为()
x
A、3个B、2个C、1个D、0个
答案:
D
考点:
二次函数的图象;反比例函数的图象。
分析:
此题实质是求函数y!
2xx2和函数讨22的图象在一、四象限有没有交点,根据
x
两个已知函数的图象的交点情况,直接判断。
2
解答:
设函数y12xx2,函数y2—
x
•••函数%2xx2的图象在一、三、四象限,开口向下,顶点坐标为(1,1),对称轴x1
2
函数y2-的图象在一、三象限;而两函数在第一象限没有交点,交点在第三象限
x
即方程2xx22的正根的个数为0个。
x
归纳:
此题用函数知识解答比较容易,主要涉及二次函数和反比例函数图象的有关性质,同
学们应该熟记且灵活掌握。
2x3
5、方程xx11的所有整数解的个数是()
A、2B、3C、4D、5
答案:
C
考点:
零指数幂。
专题:
分类讨论。
分析:
方程的右边是1,有三种可能,需要分类讨论。
第1种可能:
指数为0,底数不为0;
A、1和1B、丄和1C、1和1D、1和1
3232
答案:
B
考点:
解一元二次方程-因式分解法;一元二次方程的解.
分析:
因为方程的两个根为3和1,所以方程可以方程因式为ax3x10,用含a的
式子表示b和c,代入后面的方程可以用因式分解求出方程的根。
解答:
Tax2bxc0的两根为3和1
/•ax3x10
整理得:
ax22ax3a0
二b2a,c3a
把b,c代入方程bx2cxa0,得:
2ax23axa0
a2x1x10
1彳
--X1,x21
2
归纳:
本题考查的是用因式分解法解一元二次方程,把方程的两根代入方程,整理后用含a
的式子表示b和c,然后把b,c代入后面的方程,用因式分解法可以求出方程的根。
7、实数x、y满足x2xyy22,记ux2xyy2,则u的取值范围是()
A、2
3
u6
B、2u2C、1u6
3
D、1u2
答案:
A
考点:
完全平方公式。
专题:
综合题。
分析:
把原式的xy变为2xyxy,根据完全平方公式特点化简,
然后由完全平方式恒大于等
于0,得到
xy的范围;再把原式中的xy变为2xy3xy,冋理得到
xy的另一个氾围,求出两氾
围的公共部分,然后利用不等式的基本性质求出22xy的范围,最后利用已知x2xyy22表
示出x2y2,代入到u中得到u22xy,22xy的范围即为u的范围。
解答:
由x2xyy22得:
x22xyy22xy0
即xy22xy0,则xy2
由x2xyy22得:
x22xyy223xy0
即xy223xy0,则xy—
3
c2
2xy-
3
不等式两边同时乘以2得:
42xy4