全等三角形培优专题训练.docx

全等三角形培优专题训练.docx

《全等三角形培优专题训练.docx》由会员分享，可在线阅读，更多相关《全等三角形培优专题训练.docx（14页珍藏版）》请在冰豆网上搜索。

全等三角形培优专题训练

八年级数学培优专题训练

（二）

探索三角形全等的条件

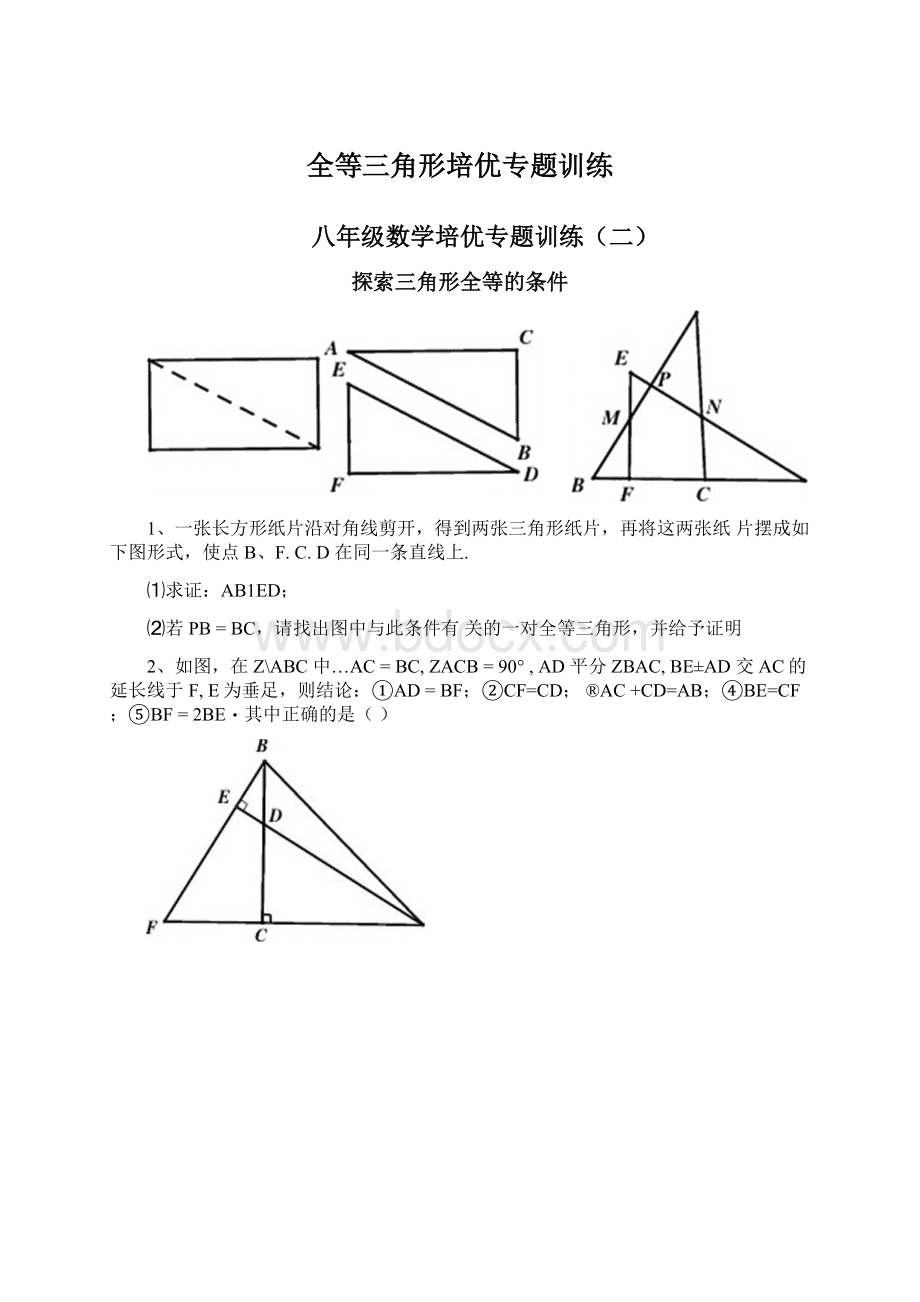
1、一张长方形纸片沿对角线剪开，得到两张三角形纸片，再将这两张纸片摆成如下图形式，使点B、F.C.D在同一条直线上.

⑴求证：

AB1ED；

⑵若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明

2、如图，在Z\ABC中…AC=BC,ZACB=90°,AD平分ZBAC,BE±AD交AC的延长线于F,E为垂足，则结论：

①AD=BF；②CF=CD；®AC+CD=AB；④BE=CF；⑤BF=2BE・其中正确的是（）

3、如图，点C在线段AB上，DA丄AB,EB丄AB,FC丄AB,且DA=BC,EB=AC,FC=AB,ZAFB=51°,求ZDFC的度数.

4、如图，四边形ABCD中，AB〃CD,AD〃BC,0为对角线AC的中点，过点0

作一条直线分别与AB、CD交于点\仁N,点E、OE=OF・

⑴图中共有几对全等三角形，请把它们都写下来；

⑵求证：

ZMAE=ZNCF

5、在Z\ABC中，高所在直线AD和BE交于H点，且BH=AC,则ZABC=

6、下列三个判断：

⑴有两边及其中一边上的高对应相等的两个三角形全等；

⑵有两边及第三边上的高对应相等的两个三角形全等；

⑶一边及其它两边上的高对应相等的两个三角形全等.

上述判断是否正确？

若正确，说明理由；若不正确，请举出反例.

八年级数学培优专题训练（三）

全等三角形的应用

全等三角形常用来转移线段和角，用它来证明：

1线段和角的等量关系

2线段和角的和差倍分关系

3直线与直线的平行或垂直等位置关系

1、如图，已知BD、CE分别是Z\ABC的边AC和AB上的高，点P在BD的延长线上，BP=AC,点Q在CE上，CQ=.AB.试判断AP与AQ的关系，并证明.

2、如图，AD是ZXABC的高，E为AC上一点，BE交AD于点F,且BF=AC,FD=CD,

求证：

BE丄AC

3、（2012・阜新中考）如图，在AABC中，AB=AC,AD=AE,ZBAC=ZDAC=90°.

⑴当点D在AC上时，如图®，线段BD,CE有怎样的数量和位置关系？

证明你猜想的结论.

⑵将图①中的ZXADE绕点A顺时针旋转a角（0°Va<90°）,如图②，线段BD、CE有怎样的数量关系和位置关系？

问明理由.

①

E

4、在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作AADE,使AD=AE,ZDAE=ZBAC,连接CE.

⑴如图①，当点D在线段BC上时，若ZBAC=90°,则ZBCE=度.

⑵设ZBAC=a,ZBCE=B

a、如图②，当点D在线段BC上移动时，a,B之问有怎样的数量关系？

请说明理由.

b、当点D在直线BC上移动时，a,B之间有怎样的数量关系？

请直接写出你的结论.

八年级数学培优专题训练（四）

辅助线作法之连接法

在几何证明中，常通过添加辅助线来构造全等三角形•常见的添加辅助线方法有：

连接法、截长补短法.倍长中线法.翻折法.旋转法以及利用特殊条件构造全等三角形等等.

1、如图，AABC的两条高BD,CE相交于点P,且PD=PE.证明：

AC=AB

2、已知AB=DE,BC=EF,ZB=ZE,AF=CD求证:

AC〃DF

3、如图，AB交CD于点0,AD.CB的延长线相交于点E,且0A=

0C,EA=EC.ZA=ZC吗？

点（）在ZAEC的平分线上吗？

八年级数学培优专题训练（五）

辅助线作法之倍长中线法

在题目条件中含有中线的问题，我们常用的辅助线就是将中线延长一倍，其目的是为了得一对全等三角形，将分散的条件集中到一个三角形中去.

1、ZXABC中，AB=5,AC=3,求中线AD的取值范围.

2、如图，在△ABC中,AD是ZBAC的平分线，又是BC上的中线

求证:

AB=AC

3、（2014•襄阳初三模拟）在ZXABC中，D是边BC上的一点,且CD=AB,ZBAD=ZBDA,AE是ZXABD的中线.

求证:

AC=2AE

6、（竞赛015）例：

已知AD是Z\ABC的中线，BE交AC于点E,交AD于点F,且AE=EF.

求证:

AC=BF

八年级数学培优专题训练（六）

辅助线作法之截长补短法

截长法：

在第三条线段上截下一段使其等于两条线段中的一条，再证明剩余部分与另一条相等.

AD）

求证：

ZB+ZD=180°

2、在四边形ABCD中,

补短法：

把两条线段中的一条补到另一条线段上去，证明所得新线段与第三条线段相等.

1、已知AC〃BD,EA,在CD上.

求证：

AB=AC+BD

3、如图，已知Z\ABC中，ZA=90°,AB=AC,D为AC的中点，AE丄BD于E,延长AE交BC于F.

求证：

ZADB=ZCDF

4、如图，ZC=90°,AC=BC,AD是ZBAC的角平分线.求证：

AC+CD=AB

12、如图，已知AB=CD=AE=BC+DE=2,ZABC=ZAED=90°求五边形ABCDE的面积.

八年级数学培优专题训练（七）

辅助线作法之利用特殊条件构造全等三角形

2、（2012•“华罗庚杯”）如图,在ZkABC中,AC=%AB,AD平分ZBAC,且AD=BD

求证:

CD丄AC

八年级数学培优专题训练（八）

全等三角形在动态几何中的运用

1、（竞赛・014・3）如图，AABC的边BC在直线1上，AC丄BC,且AC=BC.AEFP的边FP也在直线1上，边EF与边AC重合，且EF=FP.

⑴在图①中，请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系；

⑵将AEFP沿直线1向左平移到图②的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；

⑶将AEFP沿直线1向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP.BQ.你认为⑵中所猜想的BQ与AP的数量关系和位置关系还成立吗？

若成立，给出证明；若不成立，请说明理由.

八年级数学培优专题训练（九）

探究角平分线

一、知识清单

角平分线的定义：

从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线.

三角形的角平分线定义：

三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）.由定义可知，三角形的角平分线是一条线段.

角平分线性质：

1、角平分线上的点，到这个角的两边的距离相等.

2、角平分线分得的两个角相等，都等于该角的一半.

3、三角形的三条角平分线交于一点，且到各边的距离相等，这个点称为内心.

二、方法点拨

证明角平分线有两种方法：

一是运用定义证明两个角相等；二是运用角平分线的判定方法.

三、规律清单

1遇到角平分线，可从角平分线上的某一点向角的两边作垂线段（图1）.

2遇到角平分线，常可利用翻折法或截长补短法解题（图2）.

3有两条角平分线（内角或外角）交于一点，则连接该点与三角形第三个顶点的线段会平分一个內角或外角（图3）.

4有垂直于角平分线的线段，则延长这条线段以利用三线合一解题（图4）.

5遇到角内的一点到角的两边有垂线段时，就连接这点与角的顶点，看能否平分已知角（图5）.

6遇到有多条角平分线时，可尝试用整体的思想解题（图6）.

7有翻折条件时，除注意全等的结论，还应关注折线就是角平分线、是对称轴（如图7）.

8角平分线、平行线、等腰三角形三个条件中出现任意两个，常可直接得到另一个（如图8）.

图I图2

旳3

4.真题训练

1、（2011-鄂州•竞赛•018•重庆中考）如图,AABC的外角Z

ACD的平分线CP与内角ZABC的平分线BP相交于点P,若ZBPC=40°,

则ZCAP=.

2、（竞赛•019）如图,ZB=ZC=90°,M是BC的中点,DM平分ZADC.

求证:

平分ZDAB

3、（竞赛•019）如图，在△ABC中,ZBAC=90°,AB=AC,BE平分

ZABC,CE丄BE.

求证：

CE=*BD

4、如图，在AABC中，AD平分ZBAC,BD=CD

求证：

ZB=ZC

5、如图，在RtAABC中，ZC=90°,AC=BC,AD是ZBAC的平分线，交BC于D,DE丄AB于E,若AB=10cm,则ADBE的周长是多少？

6、（2011,恩施中考）AD是AABC的角平分线，DF丄AB,垂足为F,DE=DG,AADG和AAED的面积分别为50和39,则AEDF的面积为多少？

7、如图，AABC中，AD平分ZBAC,DG丄BC且平分BC,DE丄AB于E,DF丄AC于F.

求证：

BE=CF

8、在AABC中,AD是ZBAC的平分线，E.F分别为AB、AC上的点,且ZEDF+ZBAF=180°

⑴求证：

DE=DF

⑵如果把最后一个条件改为AE>AF,且ZAED+ZAFD=180°,那么结论还成立吗？

9、如图，已知AI3=AC,BE丄AC于E,CF丄AI3于F,BE与CF交于点求证：

点D在ZBAC的平分线上.

10、如图，在四边形ABCD中，对角线AC平分ZBAD,AB>AD,下

列结论正确的是（）

-AD>CB-CD

-AD=CB-CD

-AD

-CD与CB-CD的大小关系不确定

11、（竞赛014）如图，已知Z\ABC中，ZB=60°,ZBAC,ZBCA的

平分线AD,CE相交于点0.

求证：

DC+AE=AC

12、（竞赛•019）如图，已知ZiABC,P为内角平分线AD、BE、CF的交点，过点P作PG丄BC于G点。

试说明ZBPD与ZCPG的大小关系，并说明理由。

八年级数学培优专题训练（十）

应用线段垂直平分线的性质和判定解题

一、知识清单

定义：

经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

线段垂直平分线的性质：

线段垂直平分线上的点与这条线段两个端点的距离相等。

线段垂直平分的判定：

与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。