初中数学找规律专题练习.docx
《初中数学找规律专题练习.docx》由会员分享,可在线阅读,更多相关《初中数学找规律专题练习.docx(17页珍藏版)》请在冰豆网上搜索。
初中数学找规律专题练习
找规律专题练习
1、你喜欢吃拉面吗?
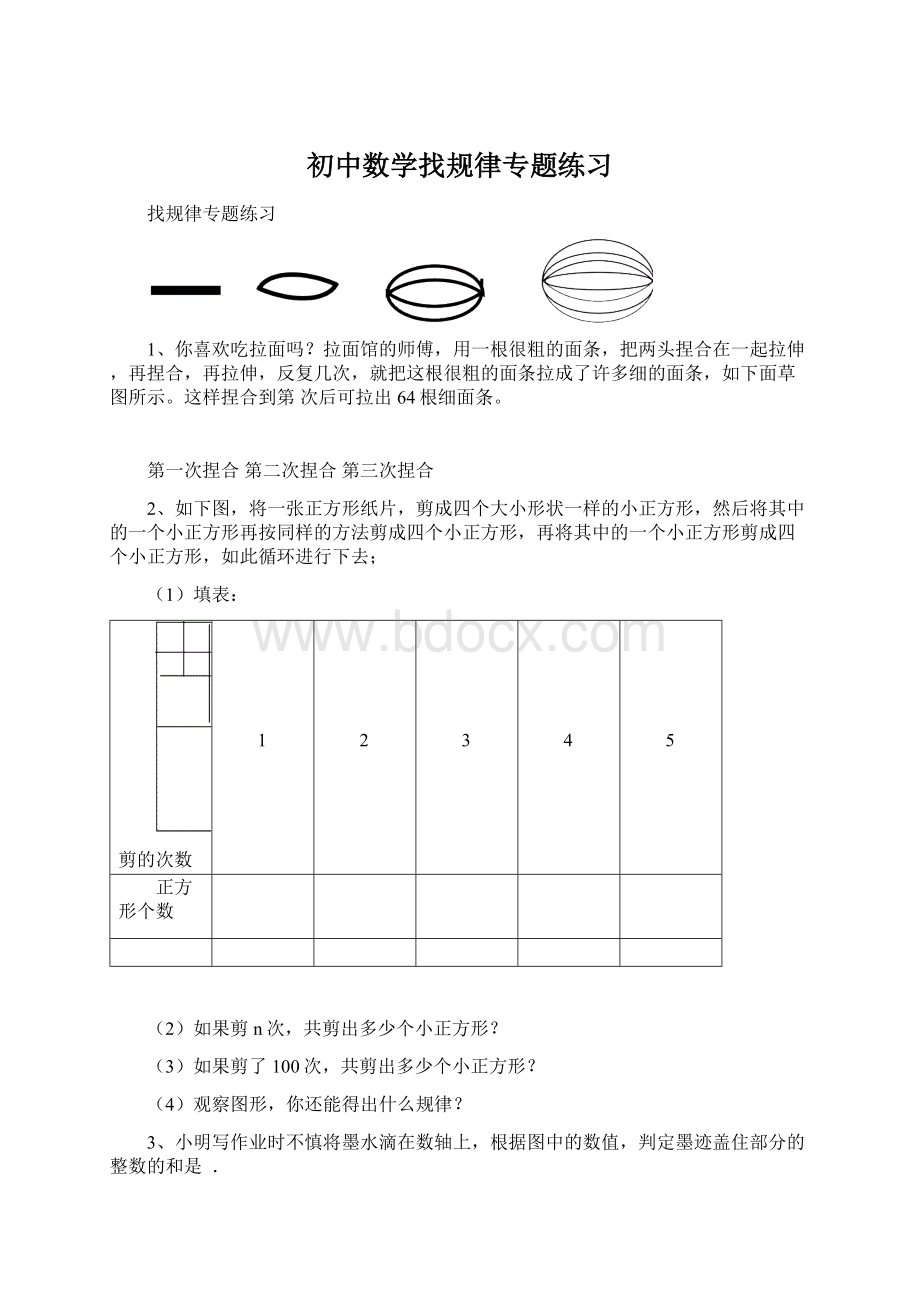
拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示。
这样捏合到第次后可拉出64根细面条。
第一次捏合第二次捏合第三次捏合
2、如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
剪的次数
1
2
3
4
5
正方形个数
(2)如果剪n次,共剪出多少个小正方形?
(3)如果剪了100次,共剪出多少个小正方形?
(4)观察图形,你还能得出什么规律?
3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是.
–6–4–3–2-101245
4、填表并回答下列问题
x
0.01
0.1
1
10
100
1000
(1)根据上表结果,描述所求得的一列数的变化规律
(2)当x非常大时,
的值接近于什么数?
5、现有黑色三角形“▲”和“△”共200个,按照一定规律排列如下:
▲▲△△▲△▲▲△△▲△▲▲……
则黑色三角形有 个,白色三角形有 个。
6、仔细观察下列图形.当梯形的个数是n时,图形的周长是.
1
11
2
7、用火柴棒按如下方式搭三角形:
(1)填写下表:
(2)照这样的规律搭下去,搭n个这样的三角形需要______根火柴棒
8、把编号为1,2,3,4,…的若干盆花按右图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为___________色.
9、已知一列数:
1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行1
第2行-2 3
第3行-4 5 -6
第4行7 -8 9 -10
第5行11-12 13 -14 15
……
按照上述规律排下去,那么第10行从左边数第5个数等于.
10、观察下列算式:
,
,
,
,请你在察规律之后并用你得到的规律填空:
第n个式子呢?
___________________
11、一张长方形桌子可坐6人,按下列方式讲桌子拼在一起。
①张桌子拼在一起可坐______人。
3张桌子拼在一起可坐____人,n张桌子拼在一起可坐______人。
②一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
③若在②中,改成每8张桌子拼成1张大桌子,则共可坐_________人。
12、用计算器计算下列各式,并将结果填写在横线上。
11×7×15873=
22×7×15873=
33×7×15873=
44×7×15873=
你发现了什么规律?
把你发现的规律用简练的语言写出来;
13、观察下列顺序排列的等式:
9×0+1=1
9×1+2=11
9×2+3=21
9×3+4=31
9×4+5=41
……
猜想:
第n个等式(n为正整数)应为.
14、一个两位数的个位数是a,十位数字是b,请用代数式表示这个两位数是__________________。
15、观察下列各式:
3
=3,3
=9,3
=27,3
=81,3
=243,3
=729…你能从中发现底数为3的幂的个位数有什么规律吗?
根据你发现的规律回答:
3
的个位数字是.
16、观察下列各式,你会发现什么规律?
3×5=15,而15=
。
5×7=35,而35=
……
11×13=143,而143=
将你猜想到的规律用只含一个字母的式子表示出来:
_______。
17、问题:
你能比较20052006和20062005的大小吗?
为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1)n的大小(n为正整数),我们从n=1,n=2,n=3……这些简单的情况入手,从中发现规律,经过归纳,猜出结论。
(1)通过计算,比较下列各组数字大小
①12______22②23______32③34________43
④45______54⑤54______65⑥67_________76
(2)把第
(1)题的结果经过归纳,你能得出什么结论?
你能用只含有一个字母的式子表示吗?
(3)根据上面的归纳猜想得到的结论,试比较两个数的大小(1分)
20052006________20062005(填”>”,”<”,“=”)
18、为了美化城市,某商场在门前的空地上用花盆按如图所示的方式搭正方形,
(1)填写下表
正方形的层数
1
2
3
4
5
花盆的个数
4
(2)按这个规律搭下去,搭第n层正方形,需要________________盆花?
19、下面有三组数,请你填上合适的运算符号,使每一组数的结果都为10。
(1)1559=10;
(2)3333=10;(3)1199=10
20、小红和小花在玩一种计算的游戏,计算的规则是
=ad-bc。
现在轮到小红计算
的值,请你帮忙算一算得多少?
21、黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比。
黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。
两只蚂蚁同时起跑,说也奇怪,两只蚂蚁同时到达了乙处。
(1)两只蚂蚁请你帮助判断:
谁跑得快?
(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?
22.
(1)3个球队进行单循环赛(参赛的每一个队都与其它所有各队比赛一场),总的比赛场数是多少?
4个球队呢?
m个球队呢?
(代数式表示出来)
(2)当m=12时,总共比赛几场?
23.按一定规律排列的一串数:
中,第98个数是_____________
14.下面的算式里,符号○、△、和□分别代表三个不同的自然数,这三个数的和是________
24.一群整数朋友按照一定的规律排成一排,可排在□位置的数跑掉了,请帮它们把跑掉的朋友找回来。
(1)5,8,11,14,□,20;
(2)1,3,7,15,31,63,□;
(3)1,1,2,3,5,8,□,21
25.下列两列数:
2,4,6,8,10,12,……1994;
6,13,20,27,34,……1994
这两列数中,相同的数的个数是( )
A、142 B、143 C、284 D、285
26.一串数字的排列规律是:
第一个数是20,从第二个数起,每一个数比前一个数小8
(1)第10个数是多少?
(2)第n个数是多少?
(3)第几个数是—60
27.某仓库堆放一批圆木,一共20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根?
28.在如图所示的2003年1月份的日历中,用一个方框圈出任意3×3个数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1)从左下角到右上角的三个数字之和为45,那么这9个数的和是多少?
这9个日期中最后一天是1月几日?
(2)用这样的方框能否圈出总和为162的9个数?
29.观察下列数据,按某种规律在横线上填上适当的数:
1,
,
,
,
,,…
30.如图,△ABC中,D是边BC上的中点,
F是线段CD的中点,E是边AC的中点,则
图中有_______条线段,有________个角,若△DEF的面积是2,则△ABC的面积是________
31.平面内两两相交的6条直线,其交点个数最少为m个,最多为n个,则m+n等于()
A、12B、16C、20D、以上都不对
32.如图,可以看成是边长为4的小正方形的巧克力糖,请你用尽可能多的不同方法把它分成形状、大小完全相同的四块,要求不把正方形糖块划破(至少五种方法)
33.在某月日历上一个竖列相邻的五个数之和为80,这五个数是______________________
34.某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是36,那么第三个日期是___________
35.今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是91,那么李老师是_________号回家的
36.如果这个月的5号是星期三,则20号是星期_________
37.三个连续偶数中,n是最小的一个,这三个数的和为_________。
38.下列图形中三角形的个数是()
A.4个B.6个C.9个D.10个
39、至少找出下列几何体的4个共同点
40、观察公式:
公式1:
公式2:
(1)这两个公式有什么特点?
(2)利用公式计算:
41、下面有三组数,请你填上合适的运算符号,使每一组数的结果都为10。
(1)1559=10;
(2)3333=10;(3)1199=10
42.造一个含有字母p和q的代数式,使得不论p、q取何值,代数式的值永远不是正的。
43.
图是2002年6月份的日历,现用一矩形在日历中任意框出4个数ab,请用一个等式表示,a、b、c、d之间的关系__________。
d
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
44.右图,是用火柴棒摆成的一个大三角形,它是由九个小三角形组成的,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形哪(每个小三角形内只填一个数),要求靠近大三角形每条边的每五个数相加的和相等,请想一想,怎样填这些数才能使五个数的和尽可能大一些,这五个数的和最大是多少?
45.王答应了大臣的一个要求:
即在国际象棋棋盘上“第1格放一粒米,第二格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到64格”。
但是不久国王九发现国库里没有这么多米,然而国王的话不能不算数,国王又不好意思向别人借,怎么办呢?
请你帮国王想一个好办法来解决这个问题。
(办法必须合乎情理,有创意者可适当多加分。
办法多者亦可多加分)
46.如果连结多边形的一边上一点与其余各顶点可将某多边形分割成2004个三角形,求该多边形的边数.
47.如图1-26,在
ABC中,点D,E,F分别是AB,BC,AC三边中点,图中与
BOD面积相等的三角形有几个?
48.观察图1-27中有几个三角形?
由此你发现三角形的个数有什么规律呢?
一个三角形3个三角形______个三角形______个三角形
_________个三角形(n个点)
49.求个数
(1)
(2)
(1)图1-28
(1)中有多少个三角形?
(2)图1-28
(2)中有多少个四边形?
50.如图1-29所示,图①是一个三角形,分别连结这个三角形三边的中点(将这条边分为相等的两部分的点)得到图②;再分别连结图②中间的小三角形三边的中点,得到图③,按此方法继续下去,请你根据图中三角形个数的规律,完成下列问题:
①②③
图1-29
(1)将下表填写完整.
图形符号
1
2
3
4
5
……..
52、下列图形经过折叠能否围成一个正方体?
(1)
(2)(3)(4)
53、某种细胞每过30分便由1个分裂成2个,经过5小时,这种细胞由1个能分裂成个。
54、有一张厚度是0.1毫米的纸,将它对折1次后,厚度为2×0.1毫米。
(1)、对折2次后,厚度为毫米。
(2)对折20次后,厚度为毫米。
(3)对折n次后,厚度为毫米。
55、下图
(1)表示1张餐桌和6张椅子(每个小半圆代表1张椅子),若按这种方式摆放20张餐桌需要的椅子张数是 。
56、观察下列算式:
根据上述算式中的规律,你认为
的末位数字是().
57、某种细菌在培养过程中,每半小时分裂1次,每次一分为二。
若这种细菌由1个分裂到16个,那么这个过程要经过()
A.1.5小时B.2小时C.3小时D.4小时
58、计算:
1-2+3-4+……+2001-2002+2003=.。
59、根据规律填上合适的数:
(1)-9,-6,-3,,3;
(2)1,8,27,64,,216;(3)2,5,10,17,,37
60、下列各图经过折叠后不能围成一个正方体的是()
(A)(B)(C)(D)
(1)
(2)(3)(4)
61、当下面这个图案被折起来组成一个正方体,数字_____会在与数字2所在的平面相对的平面上。
456
123
62、在下面的图形中()是正方体的展开图.
63、观察下列数据,按某种规律在横线上填上适当的数:
1,
,
,
,,,…
64、一列数71,72,73…72003,其中末位数是3的有个。
65、下列平面图形中不能围成正方体的是()
A、B、C、D、
66、指出下列平面图形是什么几何体的展开图(6分):
B
67、在下面的图形中,()是正方体的表面展开图.
ABC、D
68、探索规律:
用棋子按下面的方式摆出正方形
①按图示规律填写下表:
图形编号
(1)
(2)
(3)
(4)
(5)
(6)
棋子个数
②按照这种方式摆下去,摆第
个正方形需要多少个棋子?
③按照这种方式摆下去,第第
个正方形需要多少个棋子?
69、,
,
,
,
………
(1)猜想填空:
()2
()2
(2)若
试求n的值.
70、用火柴棒按下面方式搭图形,则第20个图形需要的火柴棒是根。