建模培训课程2最短路问题.docx
《建模培训课程2最短路问题.docx》由会员分享,可在线阅读,更多相关《建模培训课程2最短路问题.docx(14页珍藏版)》请在冰豆网上搜索。
建模培训课程2最短路问题
最短路径问题
一)手算
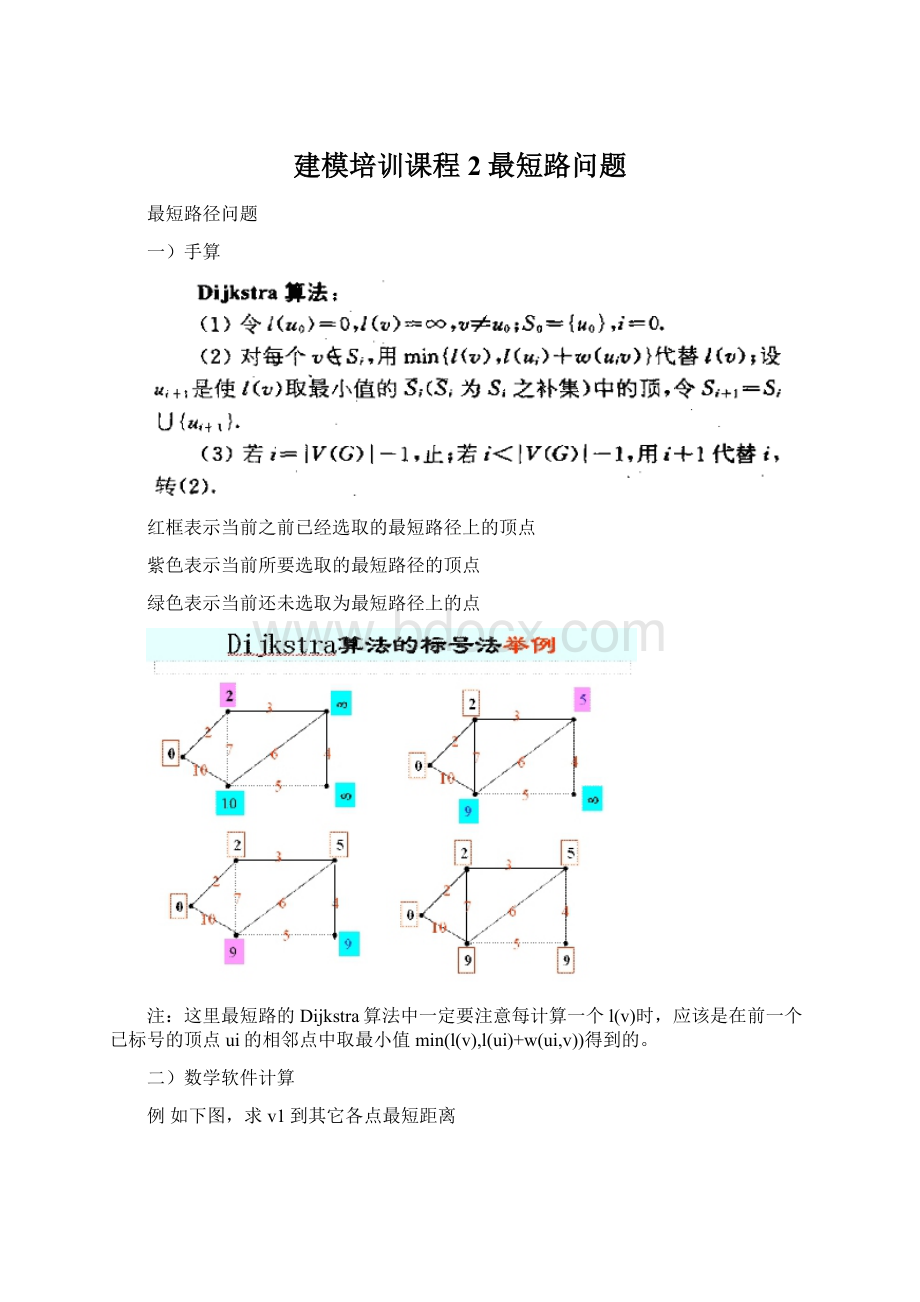
红框表示当前之前已经选取的最短路径上的顶点
紫色表示当前所要选取的最短路径的顶点
绿色表示当前还未选取为最短路径上的点
注:
这里最短路的Dijkstra算法中一定要注意每计算一个l(v)时,应该是在前一个已标号的顶点ui的相邻点中取最小值min(l(v),l(ui)+w(ui,v))得到的。
二)数学软件计算
例如下图,求v1到其它各点最短距离
(1)Matlab解法
Dijkstra算法求最短路
注意到程序中语句:
a=a+a';所以数据部分只需上三角数据。
clc,clear
a=zeros(5);
a(1,2)=10;a(1,5)=2;
a(2,3)=5;a(2,4)=6;a(2,5)=7;
a(3,4)=4;
a(4,5)=3;
a=a+a';
a(find(a==0))=inf;
pb(1:
length(a))=0;pb
(1)=1;index1=1;index2=ones(1,length(a));
d(1:
length(a))=inf;d
(1)=0;temp=1;
whilesum(pb) tb=find(pb==0);
d(tb)=min(d(tb),d(temp)+a(temp,tb));
tmpb=find(d(tb)==min(d(tb)));
temp=tb(tmpb
(1));
pb(temp)=1;
index1=[index1,temp];
temp2=find(d(index1)==d(temp)-a(temp,index1));
index2(temp)=index1(temp2
(1));
end
d,index1,index2
结果显示:
d=
09952
index1=
15423
index2=
15451
解释:
以下用c(i)表示顶点vi
1)d(i)表示c
(1)到c(i)城市间最便宜路线的票价
2)index1(i)=k表示第i个获得标号的顶点是c(k)
index1
(2)=5表示第二个获得标号的顶点是c(5),index1(3)=4,说明第三个获得标号的顶点是c(4),等等
3)index2
(2)=5表示从c
(1)到c
(2)的最短路中,在到达c
(2)前的一个城市为c(5),这时我们再可以查看c
(1)到c(5)最短路中,到达c(5)前的一个城市是多少,由index2(5)=1知c(5)前一个城市为c
(1),综上,从c
(1)到c
(2)最短路为:
c
(1)->c(5)->c
(2),对应票价为d
(2)=9,这点可以从矩阵a中得到验证,a(1,5)+a(5,2)=2+7=9
注意:
由于每一次标号顶点对应的最短路上前一个顶点都由index2给出,则一定可以把整个最短路路线标出。
4)其余几个语句的相关解释
tb=find(pb==0);%存放未标号的的顶点
d(tb)=min(d(tb),d(temp)+a(temp,tb));%计算当前未标记的顶点距离
tmpb=find(d(tb)==min(d(tb)));%获取当前最短路上的该顶点在距离矩阵d(tb)中的索引(即位置),这个索引值也正好是tb矩阵中的该顶点索引
temp=tb(tmpb
(1));%tmpb可能有多个索引,取第一个索引在tb矩阵中对应的元素,这个元素就是当前获得最短路上的顶点。
例如如果temp=6,表示顶点c6
pb(temp)=1;%对当前获得最短路顶点进行标记,以防止后面再对它考虑
(2)Lingo解法:
Lingo采用的解法是动态规划法,这里我们首先要了解一下动态规划的方法,请参考文献,此处略!
为讨论问题方便,先看三个点的情况,设F(i)表示顶点vi到v3的最短距离值,Dij表示vi与vj之间边长,假如图G为:
求各顶点到v3的最短路径及距离?
分析:
易知,记F(3)=F_3=0,对于任意i<3,F(i)=F(j)+D(i,j),此时如果等号取到,可以记P(i,j)=P_i_j=1,以表示最短路径中的一条边P(i,j)。
用lingo软件可以完全显示的表示如下:
MODEL:
TITLE动态规划法寻找最短路;
[_2]-D_1_2+F_1-F_2=0;
[_3]-D_2_3+F_2=0;
[_4]P_1_2=@IF(F_1#EQ#D_1_2+F_2,1,0);
[_5]P_2_3=@IF(F_2#EQ#D_2_3+0,1,0);
END
如果是如下情况,则同一个i,i<3时F(i)=F(j)+D(i,j)有可能因j的选择不同而得到不同,但是显然我们要求的是最短距离F(i),因此可以加一个@min函数来表示最短的意思:
用lingo则可以将这些等式关系及约束条件显示为
MODEL:
TITLE动态规划法寻找最短路;
[_2]F_1=@SMIN(D_1_2+F_2,D_1_3+0);
[_3]F_2=@SMIN(D_2_1+F_1,D_2_3+0);
[_4]P_1_2=@IF(F_1#EQ#D_1_2+F_2,1,0);
[_5]P_1_3=@IF(F_1#EQ#D_1_3+0,1,0);
[_6]P_2_1=@IF(F_2#EQ#D_2_1+F_1,1,0);
[_7]P_2_3=@IF(F_2#EQ#D_2_3+0,1,0);
[_8]P_3_1=@IF(0#EQ#D_3_1+F_1,1,0);
[_9]P_3_2=@IF(0#EQ#D_3_2+F_2,1,0);
END
如何用lingo语句来写呢?
可以如下来写:
@for(cities(i)|i#lt#n:
F(i)=@min(roads(i,j):
D(i,j)+F(j));
);
@for(roads(i,j):
P(i,j)=@if(F(i)#eq#D(i,j)+F(j),1,0)
);
显然由动态规划思想,就这个问题而言,我们应把v1改为终点v5,v2改为v1,,,,依次v5改为v4,得到如下图示,下面动态规划寻求各点到终点v5(原来的v1)的最短路径及距离
说明:
下面程序中P的作用是记录最短路径具体的路线
显然,如果P(i,j)=1,则点i到点n的最短路径的第一步是i-->j,或者说P(i,j)就是最短路径上的边,否则就不是。
由此,可方便的确定出最短路径,我们只需按顺序找出p(i,j)=1,p(j,k)=1,...,p(r,t)=1,p(t,n)=1,即可知道从i到n的最短路径为:
i->j->k->...->r->t->n;
model:
title动态规划法寻找最短路;
data:
n=5;
enddata
sets:
cities/1..n/:
F;
roads(cities,cities)/
1,21,31,41,5
2,12,3
3,13,23,4
4,14,34,5
5,15,4
/:
D,P;!
定义各城市间距离D和各城市到终点的最短距离F;
endsets
data:
D=
56710
54
643
732
102;
enddata
F(n)=0;
@for(cities(i)|i#lt#n:
F(i)=@min(roads(i,j):
D(i,j)+F(j));
);
@for(roads(i,j):
P(i,j)=@if(F(i)#eq#D(i,j)+F(j),1,0)
);
结果显示:
Feasiblesolutionfound.
Infeasibilities:
0.000000
Totalsolveriterations:
10
ModelTitle:
动态规划法寻找最短路
VariableValue
N5.000000
F
(1)9.000000
F
(2)9.000000
F(3)5.000000
F(4)2.000000
F(5)0.000000
D(1,2)5.000000
D(1,3)6.000000
D(1,4)7.000000
D(1,5)10.00000
D(2,1)5.000000
D(2,3)4.000000
D(3,1)6.000000
D(3,2)4.000000
D(3,4)3.000000
D(4,1)7.000000
D(4,3)3.000000
D(4,5)2.000000
D(5,1)10.00000
D(5,4)2.000000
P(1,2)0.000000
P(1,3)0.000000
P(1,4)1.000000
P(1,5)0.000000
P(2,1)0.000000
P(2,3)1.000000
P(3,1)0.000000
P(3,2)0.000000
P(3,4)1.000000
P(4,1)0.000000
P(4,3)0.000000
P(4,5)1.000000
P(5,1)0.000000
P(5,4)0.000000
思考题:
求v1到其余各个点的最短路
解答参考如下:
将v1和v6顶点对换
lingo程序一:
model:
title动态规划法寻找最短路;
data:
n=6;
enddata
sets:
cities/1..n/:
F;
roads(cities,cities):
D,P;!
定义各城市间距离D和各城市到终点的最短距离F;
endsets
data:
D=1007312100
7100251003
3210041005
1541006100
210010061008
100351008100;
enddata
F(n)=0;
@for(cities(i)|i#lt#n:
F(i)=@min(roads(i,j):
D(i,j)+F(j));
);
@for(roads(i,j):
P(i,j)=@if((F(i)-D(i,j)-F(j))^2#lt#0.001,1,0)
);
上面数据可以先做个预处理,可以改为如下
程序二
model:
title动态规划法寻找最短路;
data:
n=6;
enddata
sets:
cities/1..n/:
c,F;
roads(cities,cities):
D,P;!
定义各城市间距离D和各城市到终点的最短距离F;
endsets
data:
D=
100351008100
3100251007
5210041003
1005410061
810010061002
1007312100;
enddata
calc:
@for(cities(j):
c(j)=D(1,j);
D(1,j)=D(6,j);
D(6,j)=c(j);
c(j)=D(j,1);
D(j,1)=D(j,6);
D(j,6)=c(j)
);
endcalc
F(n)=0;
@for(cities(i)|i#lt#n:
F(i)=@min(roads(i,j):
D(i,j)+F(j));
);
@for(roads(i,j):
P(i,j)=@if((F(i)-D(i,j)-F(j))^2#lt#0.001,1,0)
);
注意,上面最后一条语句如果为:
P(i,j)=@if(F(i)#eq#D(i,j)+F(j),1,0)
则,路径P值全为零。
部分非零解:
Feasiblesolutionfound.
Infeasibilities:
0.2486900E-13
Extendedsolversteps:
0
Totalsolveriterations:
150
ModelTitle:
动态规划法寻找最短路
VariableValue
F
(1)8.000000
F
(2)3.000000
F(3)5.000000
F(4)8.000000
F(5)8.000000
P(1,3)1.000000
P(2,6)1.000000
P(3,2)1.000000
P(3,6)1.000000
P(4,2)1.000000
P(5,6)1.000000
附:
任意两点间最短距离-floyd算法matlab程序
%Floyd'sAlgorithm 通过一个图的权值矩阵求出它的任意两点间的最短路径矩阵。
%Floyd算法适用于APSP(AllPairsShortestPaths),是一种动态规划算法,
%稠密图效果最佳,边权可正可负。
%此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法。
function [D,path]=floyd(a)
%a为图的带权邻接矩阵
%从图的带权邻接矩阵A=[a(i,j)]n×n开始,递归地进行n次更新,
%即由矩阵D(0)=A,按一个公式,构造出矩阵D
(1);
%又用同样地公式由D
(1)构造出D
(2);……;
%最后又用同样的公式由D(n-1)构造出矩阵D(n)。
%矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度,称D(n)为图的距离矩阵,
%同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
%采用的是松弛技术,对在i和j之间的所有其他点进行一次松弛。
所以时间复杂度为O(n^3);
n=size(a,1); %计算出a的规模的大小.
D=a;path=zeros(n,n);%设置D和path的初值.
fori=1:
n
forj=1:
n
ifD(i,j)~=inf
path(i,j)=j;
end
end
end
%做n次迭代,每次迭代均更新D(i,j)和path(i,j)
fork=1:
n
fori=1:
n
forj=1:
n
ifD(i,k)+D(k,j) D(i,j)=D(i,k)+D(k,j);
path(i,j)=path(i,k);
end
end
end
end
%关于path的说明:
path(i,j)表示从i到j的最短路径中紧接着i后面的一个结点
解答如下:
由该图的带权邻接矩阵(边权矩阵)a为:
>>a=[035inf8inf
3025inf7
5204inf3
inf54061
8infinf602
inf73120]
a=
0 3 5 Inf 8 Inf
3 0 2 5 Inf 7
5 2 0 4 Inf 3
Inf 5 4 0 6 1
8 Inf Inf 6 0 2
Inf 7 3 1 2 0
然后将上述代码写入一个floyd.m文件,在命令窗口中输入:
>>floyd
>>D
D=
0 3 5 8 8 8
3 0 2 5 7 5
5 2 0 4 5 3
8 5 4 0 3 1
8 7 5 3 0 2
8 5 3 1 2 0
>>path
path=
1 2 3 2 5 3
1 2 3 4 3 3
1 2 3 4 6 6
2 2 3 4 6 6
1 6 6 6 5 6
3 3 3 4 5 6
或者直接用一个程序:
function[D,path]=floyd(a)
a=sheng;
a(find(a==0))=inf;
n=size(a,1);
D=a;path=zeros(n,n);
fori=1:
n
forj=1:
n
ifD(i,j)~=inf
path(i,j)=j;
end
end
end
fork=1:
n
fori=1:
n
forj=1:
n
ifD(i,k)+D(k,j)D(i,j)=D(i,k)+D(k,j);
path(i,j)=path(i,k);
end
end
end
end
fori=1:
n
D(i,i)=0;
path(i,i)=i;
end
functiona=sheng
a=[035inf8inf
3025inf7
5204inf3
inf54061
8infinf602
inf73120];
然后
>>[D,path]=floyd
D=
035888
302575
520453
854031
875302
853120
path=
123253
123433
123466
223466
166656
333456
解释:
比如我们看到D(1,5)=8表示v1到到v5的距离是8,再查看具体路径,path(1,5)=5,表示v1到v5最短路径中紧接着v1的下一个顶点就是v5,说明边(v1,v5)就是最短路;
再如,D(1,6)=8,path(1,6)=3,path(3,6)=6,说明v1到v6的最短距离是8,最短路为v1->v3->v6。
从D(1,6)=8=5+3=D(1,3)+D(3,6)可以得到验证。