空间几何体表面积与体积公式大全.docx
《空间几何体表面积与体积公式大全.docx》由会员分享,可在线阅读,更多相关《空间几何体表面积与体积公式大全.docx(21页珍藏版)》请在冰豆网上搜索。
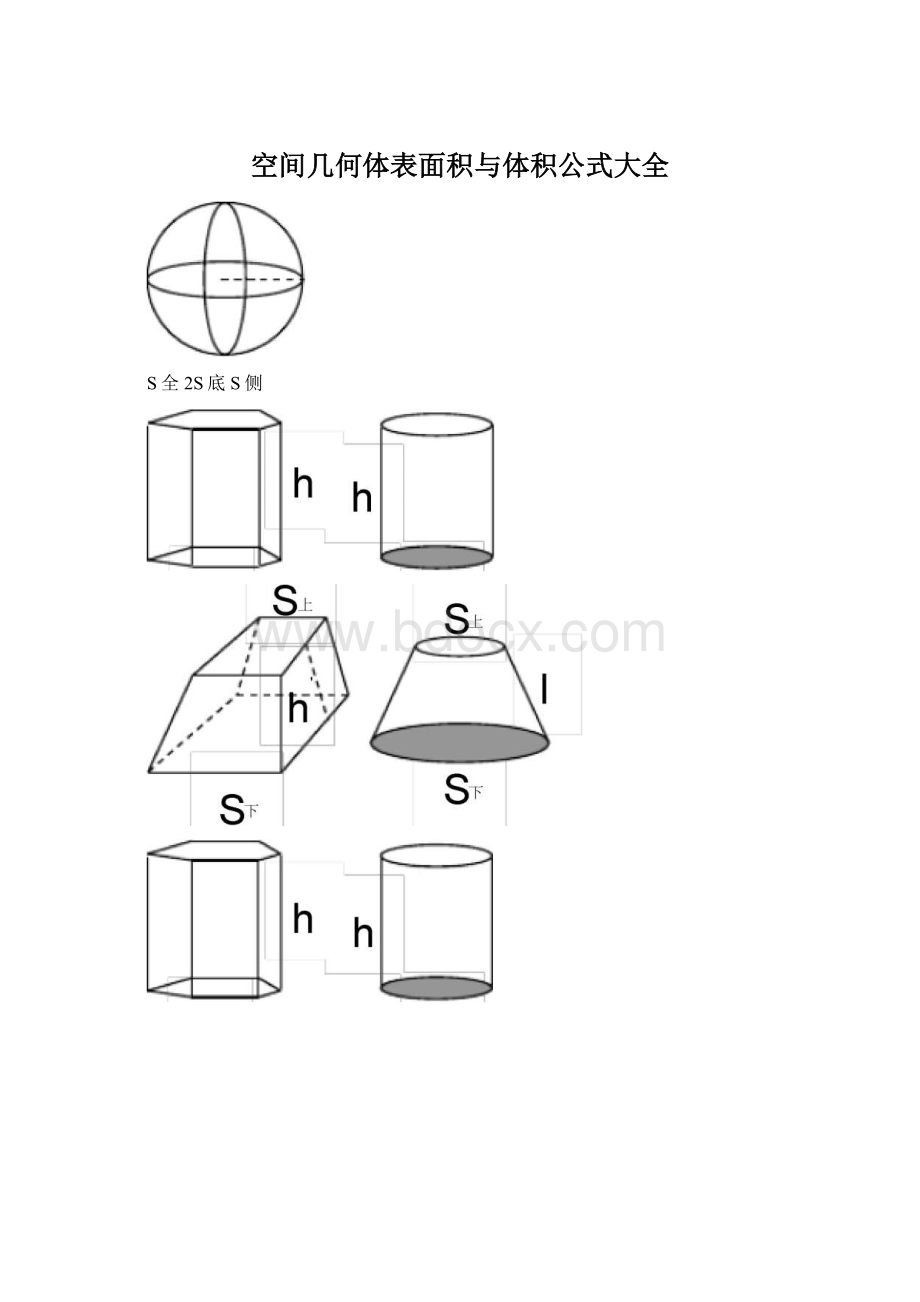
空间几何体表面积与体积公式大全
S全2S底S侧
空间几何体的表面积与体积公式大全
全(表)面积(含侧面积)
1、柱体
1棱柱]
4S侧ch
2
圆柱J
2、锥体
1棱锥:
S棱锥侧*c底h
2圆锥:
S圆锥侧托底l
3、台体
1棱口:
s棱台侧
2圆台:
s棱台侧
4、球体
1球:
S球4r2
2球冠:
略
3球缺:
略
二、体积
1、柱体
1棱柱]
卜V柱Sh
2圆柱J
2、锥体
1棱锥]1—
”V柱3Sh
2圆锥J3—
3、台体
③球缺:
略
侧面积计算时使用母线|计算三、拓展提高
1、祖暅原理:
(祖暅:
祖冲之的儿子)
夹在两个平行平面间的两个几何体,如果它们在任意高度上的平行截面面积都相等,那么这两个几何体的体积相等。
最早推导出球体体积的祖冲之父子便是运用这个原理实现的。
2、阿基米德原理:
(圆柱容球)
圆柱容球原理:
在一个高和底面直径都是2r的圆柱形容器内装一个最大的球体,则该球体的全面积等于圆柱的侧面积,体积等于圆柱体积的-。
3
分析:
圆柱体积:
V圆柱Sh(r2)2r2r3圆柱侧面积:
S圆柱侧ch(2r)2r4f因此:
球体体积:
V球-2r34r3
33
球体表面积:
S球4r2
即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体
积之和
3、台体体积公式
公式:
V台2h(S上JSS下S下)
证明:
如图过台体的上下两底面中心连线的纵切面为梯形ABCD
延长两侧棱相交于一点P。
设台体上底面积为S上,下底面积为St高为h。
易知:
PDCsPAB,设PEhi,
则pfhih
由相似三角形的性质得:
CD匹
P
ABPF
即:
—s上h_(相似比等于面积比的算术平方根)
S下hih
整理得:
hi」S±h
\SVS上
又因为台体的体积二大锥体体积一小锥体体积
.1111
二V台3ST(h1h)3S上h13h(S下S上)下h
S上h1,S上h1
代入:
h1TSHS上得:
V台^SSJS(Stz3Sth即:
V台;Sh(S下S上)3s下h3h(S上S上S下S下)
二V台3h(S上S上StSt)
4、球体体积公式推导
分析:
将半球平行分成相同高度的若干层(
n层),n越大,每一层越近似于
圆柱,n时,每一层都可以看作是一个圆柱。
这些圆柱的高为-,则:
n
每个圆柱的体积ViSh=r2丄
半球的体积等于这些圆柱的体积之和
2
220nr(r)n
2
221
r2r(r)n
2
222「3r(—r)
n
2
rn
(口
r)
•••半球体积为:
V
2
0
nr3[n
V
2
“1
{n1[(—).(—)
n
(n1)]
半球
3
nr[n
3
r[1
6(n
(1
时,
r3[1
二球体积为:
5、
1)n(2n1)
—]n
(2丄)
3
r[1
丄)(2
n
6
43
V球3r
(1
球体表面积公式推导
分析:
球体可以切割成若干(
r.22
7(r1r2
2
(口)]}
n
(n1)(2n1)
2
6n
r3(1
「n)
近似棱锥,当n时,这些棱锥的高
为球体半径,底面积为球面面积的-,则每一个棱锥的体积V1
nv
则所有的小棱锥体积之和为球体体积。
即有:
6、正六面体(正方体)与正四面体
11
3ns球r
143
(1)体积关系
如图:
正方体切下四个三棱锥后,
剩下的部分为正四面体设正方体棱长为a,则其体积为:
v正方体a3四个角上切下的每一个三棱锥体积为:
111213
V三棱锥3Sh3(2a)a6a
2猪妁1a
中间剩下的正四面体的体积为:
V正三棱锥3sh3[2(\2a)sin60](、2a)这样一个正方体可以分成四个三棱锥与中间一个正四面体即:
丄^4打3a3
6a3aa
(2)外接球
正方体与其体内最大的正四面体有相同的外接球。
(理由:
过不共面的
四点确定一个球。
)正方体与其体内最大的正面体有四个公共顶点。
所
以它们共球。
(b)正方体内切球与正四面体的四条棱相切。
(c)与正四面体四条棱相切的球半径二正方体棱长的一半
(d)设正四面体棱长为a,则与其棱都相切的球半径为ri
有.1a2
有:
r122Ta
7、利用祖暅原理推导球体体积。
构造一个几何体,使其截面与半球截面处处相等,根据祖暅原理可得两物
体体积相等。
证明:
作如下构造:
在底面半径和高都是r的圆柱内挖去一个与圆柱等底等
高的圆锥。
如图:
在半球和挖去圆锥后的组合体的相同截面上作研究,设圆柱和半球底面半径均为R,截面高度均为h,倒圆锥的截面半径为r衛,半球截面半径为
即:
S1S2,也就是说:
半球与挖去倒圆锥后有圆柱在相同的高度上有相
(1)正方体的内切球
正方体的体对角线3a
3
(d、兰3
(?
)2a
3:
2
(3)规律:
1正方体的内切球与外接球的球心为同一点;
2正方体的内切球与外接球的球心在体对角线上;
3正四面体的内切球与外接球的的半径之比为:
1:
..3
4正四面体内切球与外接球体积之比为:
1:
33
5正四面体内切球与外接球表面积之比为:
1:
3
6正方体外接球半径、正方体棱长、内切球半径比为:
、3:
2:
1
7正四面体外接球、正四面体、内切球体积比为:
3、..3:
6:
8正四面体外接球、正四面体、内切球表面积比为:
3:
6:
(1)正四面体的内切球
9、正四面体与球
解题关键:
利用体积关系思考
内切球的球心到各个面的距离相等,球心与各顶
点的连线恰好把一个正四面体分成四个三棱锥,
每个三棱锥的底面为原正四面体的底面,高为内
切球的半径r
利用体积关系得:
4(11a2sin60r)1(丄a2sin60)h
3232
所以:
r1h,其中h为正四面体的高。
由相关计算得:
2_
h『I;(;a、3)]于a
.1
…r;h
6
12a
…V正四机体:
球18:
3
(2)正四面体的外接球
(3)规律:
1正四面体的内切球与外接球的球心为同一点;
2正四面体的内切球与外接球的球心在高线上;
3正四面体的内切球与外接球的的半径之和等于高;
4正四面体的内切球与外接球的半径之比等于1:
3
5正四面体内切球与外接球体积之比为:
1:
27
6正四面体内切球与外接球表面积之比为:
1:
9
7正四面体外接球半径、正四面体棱长、内切球半径比为:
3..6:
12:
、.6
9正四面体外接球、正四面体、内切球表面积比为:
9:
6.2:
10、圆柱与球
(1)圆柱容球(阿基米德圆柱容球模型)
(2)球容圆柱
四、方法总结
下面举例说明立体几何的学习方法
思路:
先分析球心的位置。
因为正四面体是特殊的四面体,显然内切球与
外接球的球心是重合的。
且是正四面体的高线交点。
再分析球心与一些特殊的点、线、面的位置、数量关系。
在内切球这种情况下,球心垂直于每一个面,且到每一个面的距离相等;在外接球这种情况下,球心到每个顶点的距离相等。
方法1展平分析:
(最重要的方法)
如图:
取立体图形中的关键平面图形进行分析!
连接DO并延长交平面ABC于点G,连接Go连接DO并延长交BC于点E,则A、在平面AED中,由相似知识可得:
方法2:
体积分析:
(最灵活的方法)
如图:
设正四面体ABCD的内切球球心为0,连接
AO、BO、CO、DO,则正四面体被分成四个完全一样的三棱锥
设内切球半径为r,正四面体的棱长为a
则正面四体的高为:
h
a2(2、3a)卩
32
则:
4个完全一样的三棱锥体积
有:
4[3(-a2sin60)
32a
r]
兰a
12
…V内切球
6
216
V外接球
(h
3
r)
4
3(312
8
3(1
方法3:
方程分析:
(最常见的做法)
如图:
显然AO、DO是外接球半径,O。
"是内切球半径。
在Rt△DOo3中,由勾股写得可得以下方程:
2
DO
2
OOi
2
DO2i
其中:
DOi
DODOiAOi
A
B
C
D
代入方程解得:
DO
OOi
、6
a
1
4
V外接球3
3
DO
4
V内切球3
3
OOi
.6
216
方法4:
补形分析(最巧妙的思考)把正四面体补成正方体进行分析。
如图:
此时,正四面体与正方体有共同的外接球。
正四面体的棱长为a,则正方体棱长
为:
;
正方体的外接球直径为其体对角线
二正四面体的外接球半径为:
、6
4
内切球半径为:
4
V外接球3
2_6
8
4
V内切球3
36
r216
方法5:
坐标分析(最意外的解法)
建立如图所示的空间直角坐标系:
■6
则A(0,0,齐),B(0,
0),
C(1a,-6-a,0),D(1a,
0),设球心位置为
z,)
由|0A||OB||0C||OD|
R得:
2
OAOB
2
OC
2
0D
即:
:
y(z3)
(y
ya)
(X
2
1a)
2
2
a)z
=(x
1—a2
(y
解得:
z竺a
12
,即:
r
12a,
■6.66
aaa
3124
.6
8
V外接球
V内切球
43、、63
3r216a
主要方法:
1、公式的统一
对于每个几何形体的面积与体积公式,我们很想找出一个万能
公式全部适用于所有形体,但是这只是一个理想状况,实际上不可
能,最多只可能适用于一部分而已。
即使是这样,也只减小我们对公式的记忆难度,增强学习的灵活性。
(1)梯形的面积公式:
S1(ab)h,同样适用于三角形、平行四
2
边形、长方形、正方形、扇形的面积计算。
只是在使用时作微
调而已。
在分析三角形时,上底变为0;分析长方形、正方形、平行四边形时,上下底变成一样;在分析扇形时,上底变为0,下底变成弧长,高为半径。
(2)台体的侧面积公式:
s侧!
(cc)h,同样适用于圆柱、棱柱、圆锥、棱锥、球的侧面积计算。
只是在使用时作微调而已。
在
分析圆柱、棱柱时,上下底周长变成一样;在分析棱锥时,上底周长变为0;在分析圆锥时,上底周长变为0,斜高变成母
线;在分析球体的面积时,上下底都取最大圆的周长,高取直
径,即:
S球1(2r2r)2r4J
(3)台体的体积公式:
v3(s上s上S下)h,同样适用于圆
3
柱、棱柱、圆锥、棱锥、球的体积计算。
只是在使用时作微调而已。
在分析圆柱、棱柱时,上下底面积变成一样;在分析棱锥时,上底面积变为0;在分析圆锥时,上底面积变为0;在分析球体的体积时,上底面积取0,下底取最大圆面积的2倍,咼取直径,即:
s球3(2r)2r~r
2、字母的统一
在进行分析时,一般要把字母统一,这样便于进行比较!
3、关系的统一一
注意相似的关系:
面积比等于相似比的平方,体积比等于相似
比的立方。
球体、正方体、正多面体相似!
二、转换思想
1、平面与立体的转换
这是立体几何的一种重要思想,即把立体的问题交给平面来解决。
但是要在特殊的面中进行,有时还要把面与面的关系交给线与线来分析。
如二面角的大小研究,通常会作垂直于两面的交线的直线来分析。
异面直线的有关系也要平移到同一面中研究。
在立体与平面的转换中平移是一种很实用的手段。
通过平移不在同一平面内的可转换为同一平面内,不垂直的可转换为
垂直来分析!
2、位置的转换
3、
形体的转换
三、
特殊思想
1、
特殊点
(1)中点:
特殊的线的中点是解题的钥匙!
特别要关注!
(2)顶点:
几何体的顶点也是重要的点,作用。
其连线在分析时很有
(3)垂足:
高与面交点是比较特殊的点,
解题时也要注意!
2、
特殊线
(1)高线
(2)中线
(3)角平分线
3、
特殊面
(1)平行的面
(2)垂直的面
(3)二面角特殊的面
4、
特殊关系
(1)相似关系
(2)比值关系
四、
标准化思想
1、
三视图的规则
2、
斜二测画法的规则
3、
空间直角坐标规则