最新高考数学四川高考文科数学试题立几解答题优秀名师资料.docx

最新高考数学四川高考文科数学试题立几解答题优秀名师资料.docx

《最新高考数学四川高考文科数学试题立几解答题优秀名师资料.docx》由会员分享，可在线阅读，更多相关《最新高考数学四川高考文科数学试题立几解答题优秀名师资料.docx（15页珍藏版）》请在冰豆网上搜索。

最新高考数学四川高考文科数学试题立几解答题优秀名师资料

[高考数学]四川高考文科数学试题2006年—2011年立几解答题

四川高考文科数学试题2006年—2011年立几解答题

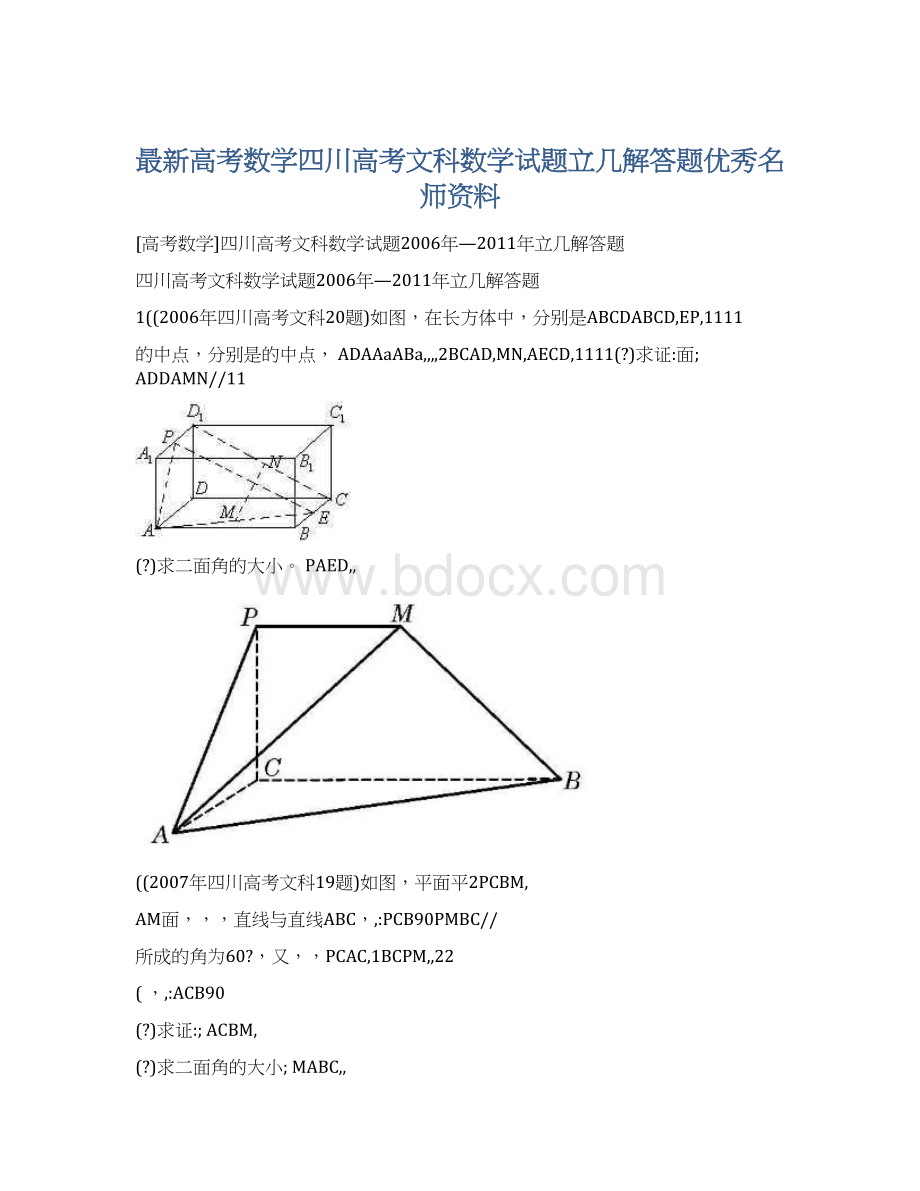
1（（2006年四川高考文科20题）如图，在长方体中，分别是ABCDABCD,EP,1111

的中点，分别是的中点，ADAAaABa,,,,2BCAD,MN,AECD,1111（?

）求证:

面;ADDAMN//11

（?

）求二面角的大小。

PAED,,

（（2007年四川高考文科19题）如图，平面平2PCBM,

AM面，，，直线与直线ABC，,:

PCB90PMBC//

所成的角为60?

，又，，PCAC,1BCPM,,22

（，,:

ACB90

（?

）求证:

;ACBM,

（?

）求二面角的大小;MABC,,

（?

）求多面体的体积（PMABC

（（2008年四川高考文科19题）如图，平面平面，四边形与3ABEF,ABEFABCD

都是直角梯形，ABCD

110////，，分别为的中点BEGH,FAFD,，,，,BADFABBC90,ADAF22,,

（?

）证明:

四边形是平行四边形;BCHG

（?

）四点是否共面,为什么,CDFE,,,

（?

）设ABBE,，证明:

平面ADE,平面;CDE

4（（2009年四川高考文科19题）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，?

ABE是等腰直角三角形，AB=AE,FA=FE,?

AEF=45?

.（?

）求证:

EF?

平面BCE;

（?

）设线段CD、AE的中点分别为P、M，求证:

PM?

平面BCE;

（?

）求二面角F-BD-A的大小.

5（（2010年四川高考文科18题）在正方体ABCD,A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.

D,（?

）求证:

OM为异面直线AA′和BD′的公垂线;C,（?

）求二面角M,BC′,B′的大小;A,B,

O,M,DC

AB

6（（2011年四川高考文科19题）如图，在直三棱柱ABC,ABC中，?

BAC=90?

，111

AB=AC=AA=1，延长AC至点P，使CP,AC，连接AP交棱CC1111111

于D（

（?

）求证:

PB?

平面BDA;11

（?

）求二面角A,AD,B的平面角的余弦值;1

四川高考文科数学试题立几答案1（（2006年四川高考文科20题）

解:

以为原点，所在直线分别为轴，轴，轴，建立直角坐标系，zDDADCDD,,yx1

则AaBaaCaAaaDa,0,0,,2,0,0,2,0,,0,,0,0,，，，，，，，，，，11

?

分别是的中点BCADAECD,,,EPMN,,,111

aaaa3,,,,,,,,?

EaPaMaNa,2,0,,0,,,,0,0,,,,,,,,,,,2242,,,,,,,,

3a,,（?

）取，显然面n,0,1,0ADDAMNa,,,0,n,，，11,,42,,

，?

又面?

面ADDAADDAMNn,,0MNn,MN,MN//1111

a,,?

过P作PHAE,，交AE于，取AD的中点F，则HF,0,0,,2,,

aaa,,,,,,设，则又Hxy,,0，，AEa,,,2,0HPxyaHFxy,,,,,,,,,,,0,,,,,,222,,,,,,

2,aa,，,,xay20,由，及在直线AE上，可得:

HAPAE,,042,

44xya，,,

332解得xaya,,,3417

8282aaaa,,,,?

?

即HFAE,HFAE,,0HPaHP,,,,,,,,,,,0,,,,17171717,,,,

PAED,,?

HP与HF所夹的角等于二面角的大小

HPHF,2cos,HPHF,,

21HPHF,

221故:

二面角的大小为PAED,,arccos21

2（（2007年四川高考文科19题）

（?

）?

平面平面，，平面（PCBM,ABCACBC,AC,ABC

平面又?

平面,?

?

BM,AC,PCBMPCBMACBM,（?

）取的中点，则（连接、（BCNCN,1ANMN?

平面平面，平面平面，（PCBMPCBM,ABCABCBC,PCBC,?

平面（?

，?

，从而平面（PMCN//MNPC//PC,ABCMN,ABC,,

作于，连结，则由三垂线定理知（MHABMH,HNHAB,

从而为二面角的平面角（，MHNMABC,,

?

直线与直线所成的角为60?

，?

（AMPC，,:

AMN60在中，由勾股定理得（,ACNAN,2

36在中，（RtAMN,MNANAMN,,，,,,cot233

AC15在中，（RtBNH,NHBNABCBN,,，,,,，,sin1AB55

6

MN303tan，,,,MHN在中，RtMNH,NH35

5

30故二面角的大小为MABC,,arctan3

（?

）如图以为原点建立空间直角坐标系（Cxyz,C

设Pz（0,0,）（0）z,，有，，（B（0,2,0）A（1,0,0）Mz（0,1,）000

AM，,由直线与直线所成的角为60?

，得AMz,,（1,1,）CPz,（0,0,）PC00

1622,即，解得（AMCPAMCP,,,,:

cos60z,zzz,，,2000032

6?

，AB,,（1,2,0）AM,,（1,1,）3

设平面的一个法向量为，则MABnxyz,（,,）1111

6,nAM,,0,，，,xyz0,,,由，取，得z,6n,（4,2,6）,,311nAB,,0,,,,，,xy20,

nn,63912取平面的一个法向量为，则n,（0,0,1）cos,,,nnABC,,,21213261,nn,12

39由图知二面角为锐二面角，故二面角的大小为（MABC,,MABC,,arccos13

（?

）多面体就是四棱锥PMABCABCPM,

1111166VVSACPMCBCPAC,,,,,,,，,,,,,，,,,（）（21）1PMABCAPMBCPMBC,3323236

3（（2008年四川高考文科19题）

由平面平面，，得平面，ABEF,AFAB,AF,ABCDABCD以为坐标原点，射线为轴正半轴，建立如图所示的直角坐标系AABxAxyz,（?

）设，则由题设得ABaBCbBEc,,,,,

ABaCabDbEacGcHbc0,0,0,,0,0,,0,0,2,0,,0,,0,0,,0,,,，，，，，，，，，，，，，，

所以HGbBCb,,0,,0,0,,0于是HGBC,，，，，

又点不在直线上所以四边形是平行四边形。

GBCBCHG

（?

）四点共面。

理由如下:

CDFE,,,

由题设知，所以Fc0,0,2，，

EFacCHacEFCH,,,,,,0.,,0.,，，，，

又，故四点共面。

CEFHFD,,,CDEF,,,

ABBE,CHaaAEaa,,,,0,,,0,（?

）由得，所以，，，，

又，因此ADb,0,2,0CHAECHAD,,,,0,0，，

即,又，所以平面ADECHAECHAD,,,ADAEA,CH,

故由平面，得平面平面ADE,CH,CDFECDE

4（（2009年四川高考文科19题）

（?

）因为?

ABE为等腰直角三角形，AB=AE，所以AE?

AB,

又因为平面ABEF?

平面ABCD，AE平面ABEF,平面ABEF平面ABCD=AB,,

所以AE?

平面ABCD,所以AE?

AD因此，AD，AB，AE两两垂直，建立如图所示的直角坐标系.设AB=1，则AE=1，BAxyz,（0，1，0），D（1，0，0），

E（0，0，1），C（1，1，0）

0因为FA=FE，?

AEF=,45

0所以?

AEF=.90

11从而，F（0，，）.,22

11.EFBEBC,,,,,,（0,,）,（0,1,1）,（1,0,0）22

11,所以EF?

BE，EF?

BC.EFBEEFBC,,，,,,,00,022

,,因为BE平面BCE，BC平面BCE，BCBE=B，所以EF?

平面BCE.……4分

1111（?

）M（0，0，）.P（1,,0）.从而PM=（，）.,1,,2222

1111于是PMEF,,,,,,,（，）（1,,0，）=02222

所以PM?

FE，又EF?

平面BCE，直线PM不在平面BCE内，

故PM?

平面BCE.………………………8分

31,BD（?

）设平面BDF的一个法向量为，并设=（x，y，z）=（1，1，0），nnBF,,（0,,）1122

xy,,0,,nBD,,0,,1即去y=1，则x=1，z=3，从=（0，0，3）n,,311,，,yz0nBF,,0,,1,,22

nn,331112取平面ABD的一个法向量为=（0，0，1）ncos,nn,,,21211||||nn,111,12

311故二面角F-BD-A的大小为.……………………….12分arccos11

5（（2010年四川高考文科18题）

以点D为坐标原点，建立如图所示空间直角坐标系D,xyz则A（1,0,0）,B（1,1,0）,C（0,1,0）,A’（1,0,1）,C’（0,1,1）,D’（0,0,1）

（1）因为点M是棱AA’的中点,点O是BD’的中点

1111所以M（1,0,）,O（,,）2222

11,,（0,0,1）,,（,1,,1,1）AA'BD'OM,,（,,0）22

11,0,，0,0OMAA'OMBD',,，22

所以OM?

AA’,OM?

BD’

又因为OM与异面直线AA’和BD’都相交

故OM为异面直线AA'和BD'的公垂线.………………………………6分

（2）两锐角的关系：

∠A＋∠B=90°；1

（2）设平面BMC'的一个法向量为,（x,y,z）,（0,,1,）,,（,1,0,1）BMnBC'12

7.同角的三角函数间的关系：

1,,nBM,0,，,yz0,,1即,取z,2,则x,2,y,1，从而,（2,1,2）n2,,1nBC'0,,,1,,，,xz0,

nn1112取平面BC'B'的一个法向量为,（0,1,0）,cosn,,,,,nn,2123||||nn9112由图可知，二面角M,BC',B'的平面角为锐角

1故二面角M,BC',B'的大小为arccos…………………12分3

②圆由两个条件唯一确定：

一是圆心（即定点），二是半径（即定长）。

6（（2011年四川高考文科19题）

13.1—3.4入学教育1加与减

（一）1P2-3如图，以A为原点，AB，AC，AA所在直线分别为x轴，y轴，z轴建立空间直角111111

扇形的面积S扇形=LR／2坐标系A,BCA，则，，，B（1,0,1），P（0,2,0）（A（0,0,0）B（1,0,0）C（0,1,0）111111

11（?

）在?

PAA中有，即（CDAA,D（0,1,）11122

化简后即为：

这就是抛物线与x轴的两交点之间的距离公式。

?

，，（AB,（1,0,1）ADx,（0,1,）BP,,（1,2,0）111

设平面BAD的一个法向量为，n,（,,）abc11

n,,，,ABac0,111,则令，则（c,,1n,,（1,,1）,112n,,，,ADbc0.,11,2

3、认真做好培优补差工作。