变压器的纵差动保护原理及整定方法.doc

变压器的纵差动保护原理及整定方法.doc

《变压器的纵差动保护原理及整定方法.doc》由会员分享，可在线阅读，更多相关《变压器的纵差动保护原理及整定方法.doc（16页珍藏版）》请在冰豆网上搜索。

热电厂主变压器的纵差动保护原理及整定方法

浙江旺能环保股份有限公司作者：

周玉彩

一、构成变压器纵差动保护的基本原则

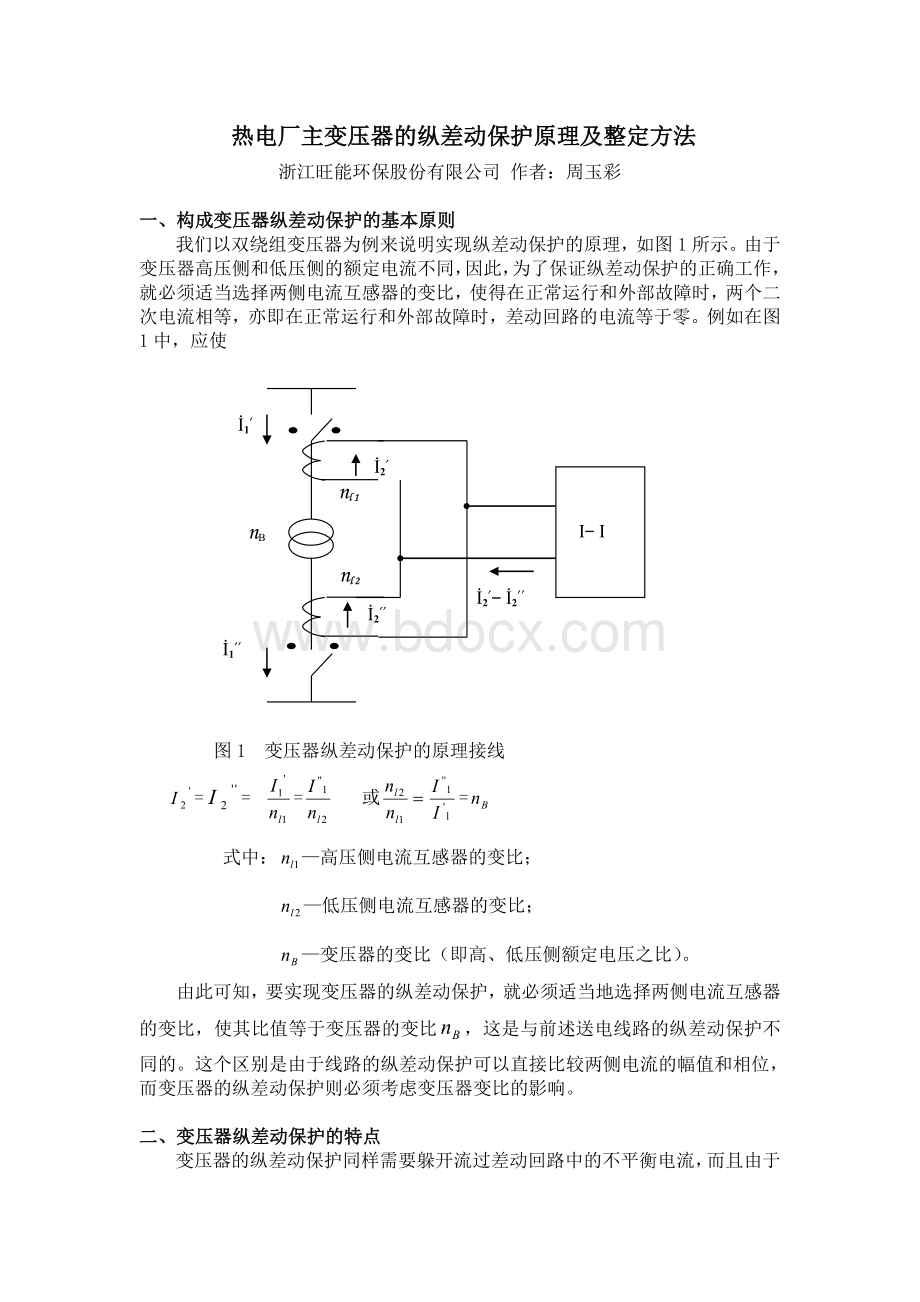
我们以双绕组变压器为例来说明实现纵差动保护的原理，如图1所示。

由于变压器高压侧和低压侧的额定电流不同，因此，为了保证纵差动保护的正确工作，就必须适当选择两侧电流互感器的变比，使得在正常运行和外部故障时，两个二次电流相等，亦即在正常运行和外部故障时，差动回路的电流等于零。

例如在图1中，应使

İ2′′

İ2′

İ1′′

nB

nl1

nl2

İ1′

İ2′-İ2′′

I-I

图1变压器纵差动保护的原理接线

===或=

式中：

—高压侧电流互感器的变比；

—低压侧电流互感器的变比；

—变压器的变比（即高、低压侧额定电压之比）。

由此可知，要实现变压器的纵差动保护，就必须适当地选择两侧电流互感器的变比，使其比值等于变压器的变比，这是与前述送电线路的纵差动保护不同的。

这个区别是由于线路的纵差动保护可以直接比较两侧电流的幅值和相位，而变压器的纵差动保护则必须考虑变压器变比的影响。

二、变压器纵差动保护的特点

变压器的纵差动保护同样需要躲开流过差动回路中的不平衡电流，而且由于差动回路中不平衡电流对于变压器纵差动保护的影响很大，因此我们应该对其不平衡电流产生的原因和消除的方法进行认真的研究，现分别讨论如下：

1、由变压器励磁涌流所产生的不平衡电流

变压器的励磁电流仅流经变压器的某一侧，因此，通过电流互感器反应到差动回路中不能平衡，在正常运行和外部故障的情况下，励磁电流较小，影响不是很大。

但是当变压器空载投入和外部故障切除后电压恢复时，由于电磁感应的影响，可能出现数值很大的励磁电流（又称为励磁涌流）。

励磁涌流有时可能达到额定电流的6~8倍，这就相当于变压器内部故障时的短路电流。

因此必须想办法解决。

为了消除励磁涌流的影响，首先应分析励磁涌流有哪些特点。

经分析得出，励磁涌流具有以下特点：

（1）包含有很大成分的非周期分量，往往使涌流偏向于时间轴的一侧；

（2）包含有大量的高次谐波，而以二次谐波为主；

（3）波形之间出现间断，在一个周期中间断角为ɑ。

根据以上特点，在变压器纵差动保护中，防止励磁涌流影响的方法有：

（1）采用具有速饱和铁心的差动继电器；

（2）利用二次谐波制动；

（3）鉴别短路电流和励磁涌流波形的差别等。

2、由变压器两侧电流相位不同而产生的不平衡电流

由于变压器常常采用Y/d－11的接线方式，因此，其两侧电流的相位差30°，二次电流由于相位不同，也会有一个差电流流入继电器。

为了消除这种不平衡电流的影响，通常都是将变压器星形侧的三个电流互感器接成三角形，而将变压器三角形侧的三个电流互感器接成星形，即用电流互感器的接线方式进行补偿。

但需注意，当电流互感器采用上述联接方式以后，在互感器接成三角形侧的差动一臂中，电流又增大了倍。

此时为保证在正常运行及外部故障情况下差动回路应没有电流，就必须将该侧电流互感器的变比加大倍，以减少二次电流，使之与另一侧的电流相等，故此时选择变比的条件是

式中和为适应Y，d接线的需要而采用的新变比。

3、由计算变比与实际变比不同而产生的不平衡电流

由于两侧的电流互感器都是根据产品目录选取标准的变比，而变压器的变比也是一定的，因此，三者的关系很难满足的要求，此时差动回路中将有电流流过。

当采用具有速饱和铁心的差动继电器时，通常都是利用它的平衡线圈来消除此差电流的影响。

4、由两侧电流互感器型号不同而产生的不平衡电流

由于两侧电流互感器的型号不同，它们的饱和特性、励磁电流也就不同，因此，在差动回路中所产生的不平衡电流也就较大。

此时应采用电流互感器的同型系数KCC=1。

5、由变压器带负荷调整分接头而产生的不平衡电流

带负荷调整变压器的分接头，是电力系统中采用带负荷调压的方法，实际上改变分接头就是改变变压器的变比。

前面已经说过，变压器的差动保护与变压器的变比有关，如果差动保护已经按照某一变比调整好（如利用平衡线圈），则当分接头改换时，就会产生一个新的不平衡电流流入差动回路。

此时不可能再用重新选择平衡线圈匝数的方法来消除这个不平衡电流，这是因为变压器的分接头经常在变，而差动保护的电流回路在带电的情况下是不能进行操作的。

因此，对由此而产生的不平衡电流，应在纵差动保护的整定值中予以考虑。

总括看来，上述5项原因中，1、2、3项是主要原因。

此外，2、3项不平衡电流可用适当地选择电流互感器二次线圈的接法和变比、以及采用平衡线圈的方法，使其降到最小。

但1、4、5各项不平衡电流，实际上是不可能消除的。

因此，变压器的纵差动保护必须躲开这些不平衡电流的影响。

由于在满足选择性的同时，还要求保证内部故障时有足够的灵敏性，这就是构成变压器纵差动保护的主要困难。

根据上述分析，在稳态情况下，为整定变压器纵差动保护所采用的最大不平衡电流可由下式确定

式中10%—电流互感器容许的最大相对误差；

—电流互感器的同型系数，取为1；

—由带负荷调压所引起的相对误差，如果电流互感器二次电流在相当于被调节变压器额定抽头的情况下处于平衡时，则等于电压调整范围的一半；

—由于所采用的互感器变比或平衡线圈的匝数与计算值不同时，所引起的相对误差；

—保护范围外部最大短路电流归算到二次侧的数值。

三、变压器纵差动保护的整定计算原则

1、变压器纵差保护

纵差保护是变压器内部故障的主保护，主要反应变压器油箱内部、套管和引出线的相间和接地短路故障，以及绕组的匝间短路故障。

1.1、对220～500kV变压器纵差保护的技术要求

a）在变压器空载投入或外部短路切除后产生励磁涌流时，纵差保护不应误动作。

b）在变压器过励磁时，纵差保护不应误动作。

c）为提高保护的灵敏度，纵差保护应具有比率制动或标积制动特性。

在短路电流小于起始制动电流时，保护装置处于无制动状态，其动作电流很小（小于额定电流），保护具有较高的灵敏度。

当外部短路电流增大时，保护的动作电流又自动提高，使其可靠不动作。

d）在最小运行方式下，纵差保护区内各侧引出线上两相金属性短路时，保护的灵敏系数不应小于2。

e）在纵差保护区内发生严重短路故障时，为防止因电流互感器饱和而使纵差保护延迟动作，纵差保护应设差电流速断辅助保护，以快速切除上述故障。

1.2、纵差保护整定计算内容

a）与纵差保护有关的变压器参数计算，包括变压器的各侧额定电流，电流互感器和中间电流互感器的变比选择等。

b）短路电流计算。

c）纵差保护动作特性参数的整定。

d）纵差保护灵敏系数的校验。

e）其他辅助验算和经验数据的推荐，包括谐波制动比（对谐波制动原理的差动保护）和闭锁角（对间断角原理的差动保护）的推荐。

1.3、纵差保护的整定计算

1.3.1.变压器参数计算

与纵差保护有关的变压器参数计算，可按表1所列的公式和步骤进行。

在表1中作了如下假定：

三绕组变压器；额定容量SN；绕组接法为YN,YN,d11；如低压侧电流互感器的二次电流最小，则选低压侧为基本侧；电流互感器二次额定电流为1A。

表1变压器参数计算表（举例）

序号

名称

各侧参数

高压侧（H）

中压侧（M）

低压侧（L）

1

额定电压UN

UNh

UNm

UNL

2

额定电流IN

3

各侧接线1）

YN

YN

d11

4

各侧电流互感器二次接线

d

d

Y

5

电流互感器的计算变比nc

6

电流互感器实际变比ns

nsh

nsm

nsL

7

各侧二次电流I

8

基本侧的选择2）

9

中间电流互感器的变比nm

1）对于通过软件实现电流相位和幅值补偿的微机型保护，各侧电流互感器二次均可按Y接线。

2）一般可选二次电流较小侧为基本侧。

1.3.2.短路电流计算

一般情况下，为整定变压器纵差保护，需作两种运行方式下的短路电流计算。

一种是在系统最大运行方式下变压器外部短路时，计算通过变压器纵差保护的最大穿越性短路电流（通常是三相短路电流），其目的是为计算差动保护的最大不平衡电流和最大制动电流。

另一种是在系统最小运行方式下，计算纵差保护区内最小短路电流（两相或单相短路电流），其目的是为计算差动保护的最小灵敏系数。

计算短路电流所采用的系统最大和最小运行方式，对于运行整定用的应由系统调度部门提供；对于设计过程中用于保护选型计算的，应由系统设计专业提供。

1.3.3.纵差保护动作特性参数的计算

带比率制动特性的纵差保护的动作特性，通常用直角坐标系上的一条折线表示。

该坐标系纵轴为保护的动作电流Iop；横轴为制动电流Ires，如图2所示。

折线ACD的左上方为保护的动作区，折线右下方为保护的制动区。

图2纵差保护动作特性曲线图

这一动作特性曲线由纵坐标OA，拐点的横坐标OB，折线CD的斜率S三个参数所确定。

OA表示无制动状态下的动作电流，即保护的最小动作电流Iop.min。

OB表示起始制动电流Ires.0。

动作特性三个参数，目前在工程实用上有两种整定计算方法，现分述如下。

a）第一种整定法：

折线上任一点动作电流Iop与制动电流Ires之比Iop/Ires＝Kres称为纵差保护的制动系数。

由图2中各参数之间的关系可导出，制动系数Kres与折线斜率S之间的关系如下式所示



（1）



（2）

从图2可见，对动作特性具有一个折点的纵差保护，折线的斜率S是一个常数，而制动系数Kres则是随制动电流Ires而变化的。

在实际应用中，是通过保护装置的参数调节整定折线的斜率来满足制动系数的要求。

1）纵差保护最小动作电流的整定。

最小动作电流应大于变压器额定负载时的不平衡电流，即

Iop.min=Krel（Ker+△U+△m）Ib2n

（3）

式中：

IN——变压器额定电流；

na——电流互感器的变比；

Krel——可靠系数，取1.3～1.５；

Ker——电流互感器的比误差，10P型取0.03×2，5P型和TP型取0.01×2；

ΔU——变压器调压引起的误差，取调压范围中偏离额定值的最大值（百分值）；

Δm——由于电流互感器变比未完全匹配产生的误差，初设时取0.05。

在工程实用整定计算中可选取IOP.min＝0.2～0.5In一般工程宜采用不小于0.3IN/na的整定值。

根据实际情况（现场实测不平衡电流）确有必要时也可大于0.5IN/na。

2）起始制动电流Ires.0的整定。

起始制动电流宜取

Iree＝（0.8～1.0）IN/na。

（4）

3）动作特性折线斜率S的整定。

纵差保护的动作电流应大于外部短路时流过差动回路的不平衡电流。

变压器种类不同，不平衡电流计算也有较大差别，下面给出普通双绕组和三绕组变压器差动保护回路最大不平衡电流Iunb.max计算公式。

双绕组变压器

Iunb.max=（Kap×Kcc×Ker+△U+△m）Ik.max/n

（5）

式中：

Ker，ΔU，Δm，na的含意同式（5），但Ker＝0.1；

Kcc——电流互感器的同型系数，Kcc＝1.0；

Ik.max——外部短路时，最大穿越短路电流周期分量；

Kap——非周期分量系数，两侧同为TP级电流互感器取1.0；两侧同为P级电流互感器取1.5～2.0。

三绕组变压器（以低压侧外部短路为例说明之）

Iunb.max＝KapKccKerIk.max/na+ΔUhIk.h.max/na.h+ΔUmIk.m.max/na.m

+Δm1Ik.Ⅰ.max/na.h+Δm1Ik.Ⅱmax/nam（6）

式中：

Kap，Kcc,Ker含意同式（5）；

ΔUh,ΔUm——变压器高、中压侧调压引起的相对误差（对UN而言）取调压范围中偏离额定值的最大值；

Ik.max——低压侧外部短路时，流过靠近故障侧电流互感器的最大短路电流周期分量；

Ik.h.max,Ik.m.max——在所计算的外部短路时，流过高、中压侧电流互感器电流的周期分量；

Ik.Ⅰ.max,Ik.Ⅱ.max——在所计算的外部短路时，相应地流过非靠近故障点两侧电流互感器电流的周期分量；

na、na.h、na.m——各侧电流互感器的变比；

ΔmⅠ、ΔmⅡ——由于电流互感器（包括中间互流器）的变比未完全匹配而产生的误差。

差动保护的动作电流

Iop.max＝KrelIunb.max（7）

最大制动系数

 Sres.max=（8）

式（8）中最大制动电流Ires.max的选取，因差动保护制动原理的不同以及制动线圈的接线方式不同而会有很大差别，在实际工程计算时应根据差动保护的工作原理和制动回路的接线方式而定。

制动线圈的接线原则是使外部故障时制动电流最大，而内部故障时制动电流最小。

当制动线圈数比变压器绕组少，不可能将每侧电流分别接入制动线圈时，可以将几个无源侧电流合并后接入制动线圈，但不应将几个有源侧电流合并接入制动线圈。

根据Iop.min、Ires.0、Ires.max、Kres.max按式

（1）可计算出差动保护动作特性曲线中折线的斜率S，当Ires.max＝Ik.max时有

S=

（9）

b）第二种整定法：

此法不考虑负荷状态和外部短路时电流互感器误差Ker的不同，使不平衡电流完全与穿越性电流成正比变化，如图3所示，比率制动特性CD通过原点，从而制动系数Kres为常数；当Kres和Ires.0确定后，Iop.min随之确定，不必另作计算。

此法计算简单，安全可靠，但偏于保守。

图3第一种整定法纵差保护动作特性曲线图

1）按下式计算制动系数Kres，即

Kres＝Krel（KapKccKer+ΔU+Δm）＝S

式中：

Krel、Kap、Kcc、Ker、ΔU、Δm的含意及取值同式（3）但Ker＝0.10。

2）画一条通过坐标原点斜率为Kres的直线OD（见图3），在横坐标上取OB＝（0.8～1.0）IN/na，此即起始制动电流Ires.0。

3）在直线OD上对应Ires.0的C点纵坐标值OA为最小动作电流Iop.min。

折线ACD即为差动保护的动作特性曲线。

上述两种整定方法中，如果Iop.min和折线（CD）斜率S的整定不是连续调节的，则Iop.min和S的整定值应取继电器能整定的，并略大于计算值的数值。

1.3.4.灵敏系数的计算

纵差保护的灵敏系数应按最小运行方式下差动保护区内变压器引出线上两相金属性短路计算。

图4为纵差保护灵敏系数计算说明图。

根据计算最小短路电流Ik.min和相应的制动电流Ires，在动作特性曲线上查得对应的动作电流I′op，则灵敏系数为

Ksen=I

（2）d.mn/IOP（10）

要求Ksen≥2。

图4纵差保护灵敏系数计算说明图

1.3.5.纵差保护的其他辅助整定计算及经验数据的推荐

a）差电流速断的整定。

对220～500kV变压器，差电流速断是纵差保护中的一个辅助保护。

当内部故障电流很大时，防止由于电流互感器饱和引起纵差保护延迟动作。

差电流速断的整定值应按躲过变压器初始励磁涌流或外部短路最大不平衡电流整定，一般取

IOP=6Ib2n

式中：

Iop——差电流速断的动作电流；

Ib2n—变压器的额定电流；

K——倍数，视变压器容量和系统电抗大小，K推荐值如下：

6300kVA及以下7～12；

6300～31500kVA4.5～7.0；

40000～120000kVA3.0～6.0；

120000kVA及以上2.0～5.0；

容量越大，系统电抗越大，K取值越小。

按正常运行方式保护安装处二相短路计算灵敏系数，

Ksen≥1.2。

Iunb.max见式（5）和式（6）。

b）二次谐波制动比的整定。

在利用二次谐波制动来防止励磁涌流误动的纵差保护中，谐波制动回路可以单独整定。

整定值可用差电流中的二次谐波分量与基波分量的比值表示，通常称这一比值为二次谐波制动比。

根据经验，二次谐波制动比可整定为15%～20%。

四、许继：

WBH-821变压器保护逻辑框图

1、比率差动保护逻辑框图如图5所示：

图5比率差动保护逻辑框图

2、差动速断保护逻辑框图6所示：

当任一相差动电流大于差动速断整定值时瞬时动作于出口，速断动作时间：

不大于20ms（1.5倍动作电流下）。

图6差动速断保护逻辑框图

3、差流越限告警逻辑框图7所示：

正常情况下监视各相差流，如果任一相差流大于差流越限定值（一般设为最小动作电流的1/2），经延时起动告警继电器。

逻辑框图如图7所示：

图7差流越限告警逻辑框图

五、某热电厂主变压器比率差动微机保护整定实例

1、发电机参数表2（#1、＃2发电机）

厂、站名称

**热电

机号

#1、#2发电机

额定容量

158.8MVA

型式

QF-138-2-13.8

0.9（滞后）

额定功率

135MW

功率因数

0.85

额定电流

6645A

额定电压

13.8KV

次暂态电抗xd”

17.64%

暂态电抗xd’

22.4%

同步电抗xd

170.64%

负序电抗x2

19.69%

零序电抗x0

7.53%

2、主变压器参数表3（#1、＃2主变）

厂名

**热电

投产日期

容量

160MVA

相数

3相

电压比

242KV±2*2.5%/13.8KV

接线

YNd11

电流

382/6694A

调压方式

铜线无激

磁调压

型式

SFP10－160000/220

制造厂

***变压器有限责任公司

阻抗电压

13.8%

备注

Sn=160MVASb=100MVA

3、短路电流计算

3.1.短路电流计算网络等效阻抗如图，电网对本电厂系统阻抗为归算至某电厂220KV母线上的阻抗,为一点等值：

a.等值方式：

不含本电厂220KV＃2发变机组.

b.系统正常运行大方式（不包括变压器）:

ZP1=0.0165；ZP0=0.0269

c.系统正常运行小方式（不包括变压器）:

ZP1=0.0271；ZP0=0.0453

d.以Se=100MVA、Ue=230KV为基准值的标幺值.

e.数据格式：

正序/零序.

f.网络等效阻抗图

升压变压器电抗:

X*1B=10Ud%*Sj/Sn=13.31×103/160000=0.0832；

发电机电抗:

X*U=（X,,d%/100）×（Sj×COSø/Pe）=17.64%×100×0.85/135

=0.1111

高厂变电抗:

X*2B=10Ud%*Sj/Se=10.19×103/20000=0.5095

厂变低压侧至出线断路器之间有4根3×240mm2长度为105米的铜芯电缆；其参数为：

电缆线路电抗:

X*L=X×L×Sj/U2p=0.08×0.105×100/4×6.32=0.0053

X0*=0.35×X*L=0.001855

图8、大方式下正序网络等效阻抗图

图9、小方式下正序网络等效阻抗图

由于封闭母线尺寸较短,截面大,阻抗值太小,本工程忽略不计.对6KV出线段，本阻抗图只列出其中一回。

3.2.运行小方式下,d1发生三相金属性短路电流：

a.发电机1G供给短路电流：

X*=0.1111+0.0832=0.1943；

X*js=X*×Sn/Sj=0.1943×158.8/100=0.308

由X*js=0.308在短路电流运算曲线查得I*=3.4；

发电机额定电流（基准电压为230KV）：

I*j=Sn/√3×Uf,n=158.8/√3×230=0.399KA

I（3）d1=I*j×I*d=3.4×0.399=1.35KA

b.220KV系统供给的短路电流：

X*L=0.0271

Ij=Sj/√3Up=100/√3×230=0.251

I（3）d.min=Ij/X*Σ=0.251/0.0271=9.26KA

3.3.运行小方式下,d2发生三相金属性短路短路电流：

a.发电机1G供给短路电流：

X*js=X*×Sn/Sj=0.1111×158.8/100=0.1764

由Xjs=0.1764在短路电流运算曲线查得I*=6.2；

I*j=Sn/√3×Uf,n=158.8/√3×13.8=6.644KA

I（3）d1=6.2×6.64=41.2KA

b.220KV系统供给的短路电流：

X*Σ=0.0271+0.0832=0.1103

Ij=Sj/√3Up=100/√3×13.8=4.18

I（3）d.min=Ij/X*Σ=4.18/0.1103=37.89KA

3.4.运行小方式下,d3发生三相金属性短路短路电流：

X*=[（0.0271+0.0832）//0.1111]+0.5095+0.0053

=0.0553+0.5095+0.0053

=0.0553+0.5148=0.5701

Ij=Sj/√3Up=100/√3×6.3=9.16

I（3）d.min=Ij/X*Σ=9.16/0.5701=16.06KA

3.5.运行大方式下,d1发生三相金属性短路电流：

X*=（0.0165）//（0.1111+0.0832）=0.0152

I（3）d.min=Ij/X*Σ=0.251/0.0152=