专题05 与角平分线垂线等腰三角形相关辅助线添加题型解读解析版.docx

专题05 与角平分线垂线等腰三角形相关辅助线添加题型解读解析版.docx

《专题05 与角平分线垂线等腰三角形相关辅助线添加题型解读解析版.docx》由会员分享，可在线阅读，更多相关《专题05 与角平分线垂线等腰三角形相关辅助线添加题型解读解析版.docx（15页珍藏版）》请在冰豆网上搜索。

专题05与角平分线垂线等腰三角形相关辅助线添加题型解读解析版

专题05与角平分线、垂线、等腰三角形相关辅助线添加题型解读

一、基础知识点综述

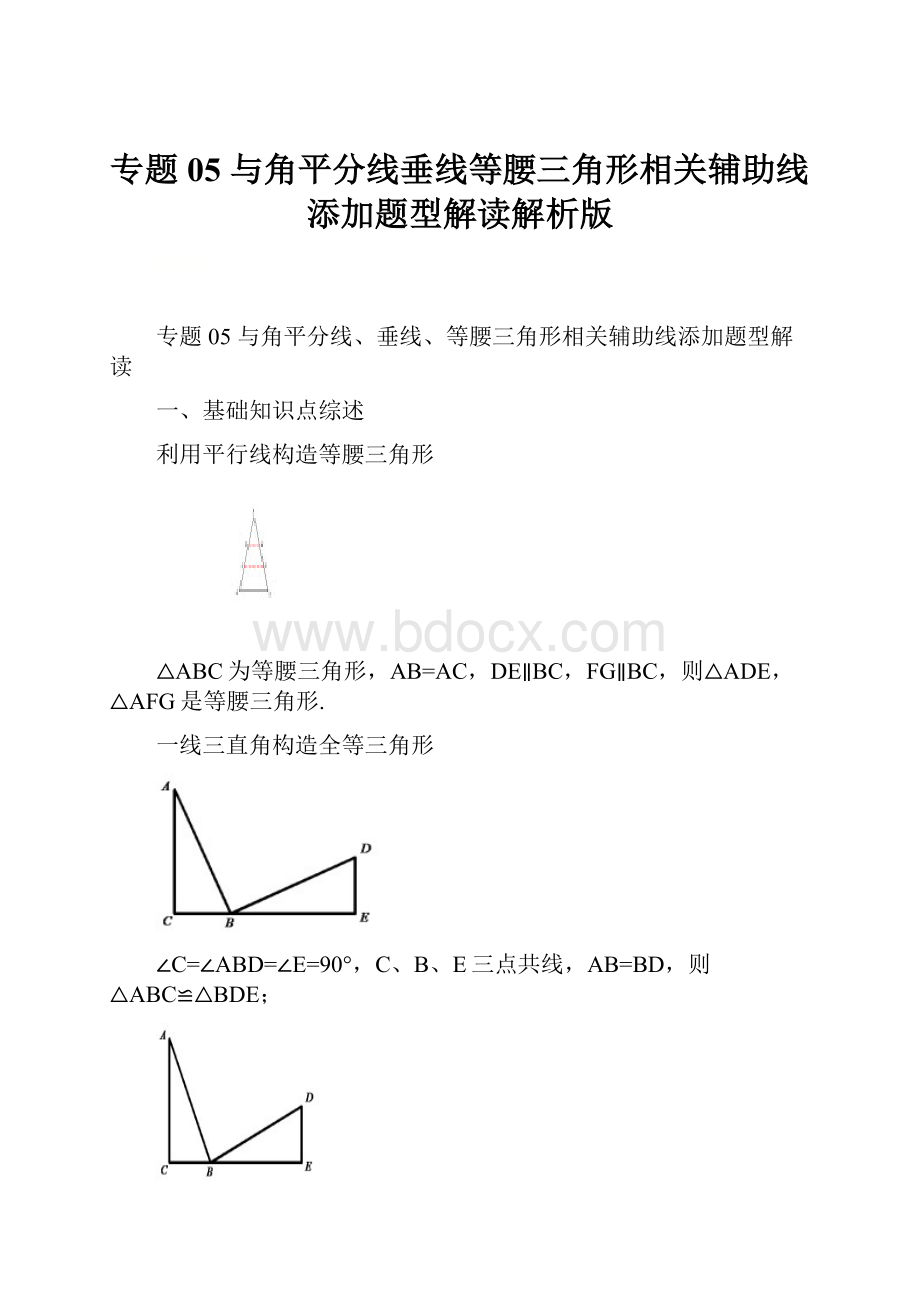
利用平行线构造等腰三角形

△ABC为等腰三角形，AB=AC，DE∥BC，FG∥BC，则△ADE，△AFG是等腰三角形.

一线三直角构造全等三角形

∠C=∠ABD=∠E=90°，C、B、E三点共线，AB=BD，则△ABC≌△BDE；

∠C=∠EAD=90°，C、A、E三点共线，DE⊥AB，AB=DE，则△ABC≌△DEA；

过角平分线上点向角两边作垂线段

二、典型例题解析

题型一：

利用角平分线性质解题题型

例1.（2019·深圳期中）如图，在△ABC中，∠BAC=40°，∠ACB=60°，D为△ABC外一点，DA平分∠BAC，∠CBD=50°，求∠DCB的度数.

【答案】见解析.

【解析】解：

如图，过D作DH⊥AB于H，DE⊥AC于E，DF⊥BC于F，

∵∠PBC=∠BAC+∠ACB=100°，∠CBD=50°，

∴∠DBC=∠DBH，

∴DF=DH，

∵DA平分∠CAB，DH⊥AB，DE⊥AC，

∴DE=DH，

∴DE=DF，

∴CD平分∠BCE，

∵∠QCB=120°，

∴∠DCB=60°.

题型二：

一线多用

例2.（2017·北京中考）在等腰直角△ABC中，∠ACB=90°，点P是线段BC上一动点（与点B,C不重合），连接AP，延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交直线AB与点M。

（1）若∠PAC=α，求∠AMQ的大小（用含α的式子表示）

（2）用等式表示线段MB与PQ之间的数量关系，并证明.（可用结论：

等腰直角三角形斜边长等于腰长的

倍.）

【答案】见解析.

【解析】解：

（1）∠AMQ=45°+α；理由如下：

∵∠PAC=α，△ACB是等腰直角三角形，

∴∠BAC=∠B=45°，∠PAB=45°-α，

∵QH⊥AP，

∴∠AHM=90°，

∴∠AMQ=180°-∠AHM-∠PAB=45°+α；

（2）如图，连接AQ，过M作ME⊥BC于E，

∵AC⊥PQ，QC=PC，

∴∠QAC=∠PAC=α，

∴∠QAM=45°+α=∠AMQ，

∴AP=AQ=QM，

∴△APC≌△QME，

∴PC=ME，

由△MEB是等腰直角三角形，

得

即PQ=

MB.

例3.（2019·河南平顶山周练）在△ABC中，∠BAC=90°，AB=AC，BD平分∠ABC，过C作CE⊥BD，交BD延长线于E，AF⊥BD于F，求证：

BD=2CE.

【答案】见解析.

【解析】证明：

如图，延长BA，CE交于点H，

∵BE⊥CH，

∴∠BEC=∠BEH=90°，

∵BE平分∠ABC，

∴∠HBE=∠CBE，

∵BE=BE，

∴△BEH≌△BEC，

∴CE=EH，CH=2CE，

∵∠BAD=∠CAH=90°，

∴∠H+∠ACH=90°，∠H+∠ABD=90°，

∴∠ACH=∠ABD，

∵AB=AC，

∴△ABD≌△ACH，

∴BD=CH=2CE.

例4.如图所示，线段AB、CD交于点E，且AB⊥BD于B，AC⊥CD于C.

（1）如图1，若AB=CD，∠D=30°，探究线段DE与CE的数量关系，并说明理由.

（2）如图2，若AB=BD，∠D=22.5°，探究线段DE与AC的数量关系，并说明理由.

图1图2

【答案】见解析.

【解析】证明：

（1）DE=2CE，

连接AD，如图，

∵AB⊥BD，AC⊥CD，

∴∠C=∠B=90°，

在Rt△ADC和Rt△DAB中，

∵AB=CD，AD=AD，

∴Rt△ADC≌Rt△DAB，

∴AC=BD，

∵∠BDE=30°，

∴∠BED=∠CEA=60°，∠CAE=30°，DE=2BE，

∴△ACE≌△DBE，

∴AE=DE，CE=BE，

∴DE=2CE.

（2）连接AD，延长DB，AC交于点H，

∵AB=BD，∠ABD=90°，

∴∠DBA=∠BAD=45°，

∵∠BDE=22.5°，

∴∠CDA=22.5°，

∵AC⊥CD，

∴∠ACD=∠DCH=90°，

∵CD=CD，

∴△ACD≌△HCD，

∴AH=2AC，

∵∠CAE+∠CEA=90°，∠BDE+∠DED=90°，∠CEA=∠DEB，

∴∠CAE=∠BDE，

∵AB=BD，∠ABD=∠EBD=90°，

∴△ABH≌△DBE，

∴DE=AH=2AC.

题型三：

一线三直角

例5.（2019·广东期末）如图，已知等腰直角△ABC中，AB=AC，∠BAC=90°，点A，B分别在x轴、y轴上，点C的坐标为（6,2），求A点、B点坐标.

【答案】见解析.

【解析】解：

过点C作CH⊥x轴于H，

∵∠CHA=∠AOB=∠BAC=90°，

∴∠CAH+∠ACH=90°，∠CAH+∠BAO=90°，

∴∠ACH=∠BAO，

∵AB=AC，

∴△ABO≌△CAH，

∴CH=OA=2，OB=AH=OH－OA=4，

即A（2,0），B（0,4）.

例6.（2018·柘城实验中学月考）如图1，在平面直角坐标系中，

.

（1）求证：

AB=CD，AB⊥CD；

（2）如图2，以A为直角顶点在第二象限内作等腰直角三角形ABE，过点E作EF⊥x轴于点F，求点F的坐标；

（3）如图3，若点P为y轴正半轴上一动点，以AP为直角边作等腰直角三角形APQ，点Q在第一象限，∠APQ=90°，QR⊥x轴于点R，当点P运动时，OP－QR的值是否发生变化？

若不变，求出其值；若变化，请说明理由。

图1图2图3

【答案】见解析.

【解析】解：

（1）证明：

由题意知，OA=2，OB=3，OC=3，OD=2，

即OA=OD，OB=OC，

∵∠AOB=∠COD=90°，

∴△AOB≌△DOC，

∴AB=CD，∠OCD=∠ABO，

延长CD交AB于H，

∵∠BAO+∠ABO=90°，

∴∠BAO+∠OCD=90°，

即∠CHA=90°，

∴AB⊥CD.

（2）∵△AEB是等腰直角三角形，

∴AB=AE，∠EAB=90°，

∴∠EAF+∠BAO=90°，

∵∠EAF+∠AEF=90°，

∴∠BAO=∠AEF，

∵∠EFA=∠AOB=90°，

∴△AEF≌△BAO，

∴AF=OB=3，

∴OF=5，即F（－5,0）.

（3）OP－QR=2，理由如下，

过点Q作QG⊥y轴于G，

∵△APQ是等腰直角三角形，∠APQ=90°，

∴AP=PQ，∠APO+∠QPG=90°，

∵∠APO+∠PAO=90°，

∴∠QPG=∠PAO，

∵∠AOP=∠QGP=90°，

∴△APO≌△PQG，

∴OA=PG=2，

∵QR⊥x轴，

∴QR=OG，

∴OP－QR=OP－OG=PG=OA=2.

例7.如图，在四边形ABCE中，AB=BC，AB⊥BC，CE⊥AE，BD⊥AE.

猜想线段BD、CE、AD之间的数量关系，并说明理由.

【答案】见解析.

【解析】解：

BD-CE=AD，理由如下，

过C作CF⊥BD于F,

∵AB⊥BC，CF⊥BD，

∴∠ABC=90°，∠CFB=90°，

∴∠ABD+∠CBF=90°，∠BCF+∠CBF=90°，

∴∠ABD=∠BCF，

∵AB=BC，

∴△ABD≌△BCF，

∴AD=BF，

∵CE⊥AE，BD⊥AE，

∴∠E=90°，∠BDE=90°，

∴四边形DECF是矩形，

∴CE=DF，

∴BD－DF=BF，

即BD-CE=AD.

题型四：

通过平行线构造等腰三角形

例8.如图，等边△ABC中，D是AC上，延长BC至E,使CE=AD,连接DB,DE，DF⊥BC于F。

（1）如图1，若D是AC的中点，求证：

DB=DE，BF=EF

（2）如图2，若点D是边AC上的任意一点，BF=EF是否仍然成立？

请证明你的结论；

（3）如图3，若点D是边AC的延长线上的任意一点，其它条件不变，

（2）中结论是否仍然成立？

画图并证明你的结论.

【答案】见解析.

【解析】解：

（1）证明：

∵△ABC是等边三角形，

∴AB=BC，∠ACB=60°，

∵D是AC中点，

∴AD=CD，BD⊥AC，∠ABD=∠CBD=30°，

∵CE=AD，

∴CE=CD，

∴∠E=∠CDE=30°，

∴∠E=∠DBC，

∴BD=DE，

∵DF⊥BE,

∴BF=EF；

（2）过D作DH∥BC交AB于H，

∵△ABC是等边三角形，DH∥BC，

∴∠ADH=∠AHD=∠A=60°，

∠BHD=∠DCE=120°，

即△ADH是等边三角形，AD=DH=AH，

∴BH=DC，

∵CE=AD，

∴CE=DH，

∴△BDH≌△DEC，

∴BD=DE，

∵DF⊥BE，

∴BF=EF.

（3）过D作DH∥BC交AB延长线于H，

∵△ABC是等边三角形，DH∥BC，

∴∠ADH=∠AHD=∠A=60°，

∠BHD=∠DCE=60°，

即△ADH是等边三角形，AD=DH=AH，

∴AH－AB=AD－AC，即BH=CD，

∵CE=AD，

∴CE=DH，

∴△BDH≌△DEC，

∴BD=DE，

∵DF⊥BE，

∴BF=EF.

例9.如图，在等边三角形ABC中，AB=10，动点P从点A出发向点C运动，Q从点B出发以相同的速度沿CB的延长线运动，连接PQ交AB于点E，作PD⊥AB于D，试探究线段DE的长度是否发生变化，若不变化，求出该值，若变化，说明理由.

【答案】见解析.

【解析】解：

DE的长度不变，DE=5，理由如下，

过P作PH∥BC交AB于H，

∵△ABC是等边三角形，

∴∠A=∠C=∠ABC=60°，AB=AC=BC，

∵PH∥BC，

∴∠AHP=∠APH=60°，∠HPE=∠BQE，

∴△AHP是等边三角形，AH=AP=PH，

∵P、Q速度相同，

∴AP=BQ，

∴BQ=PH，

∵∠PEH=∠QEB，

∴△BQE≌△HPE，

∴EH=BE，

∵△APH是等边三角形，PD⊥AH，

∴AD=DH，

∴DE=DH+EH=

AB=5.