公务员行测高分宝典.docx

公务员行测高分宝典.docx

《公务员行测高分宝典.docx》由会员分享，可在线阅读，更多相关《公务员行测高分宝典.docx（96页珍藏版）》请在冰豆网上搜索。

公务员行测高分宝典

行政能力测试题型的规律和解决方法

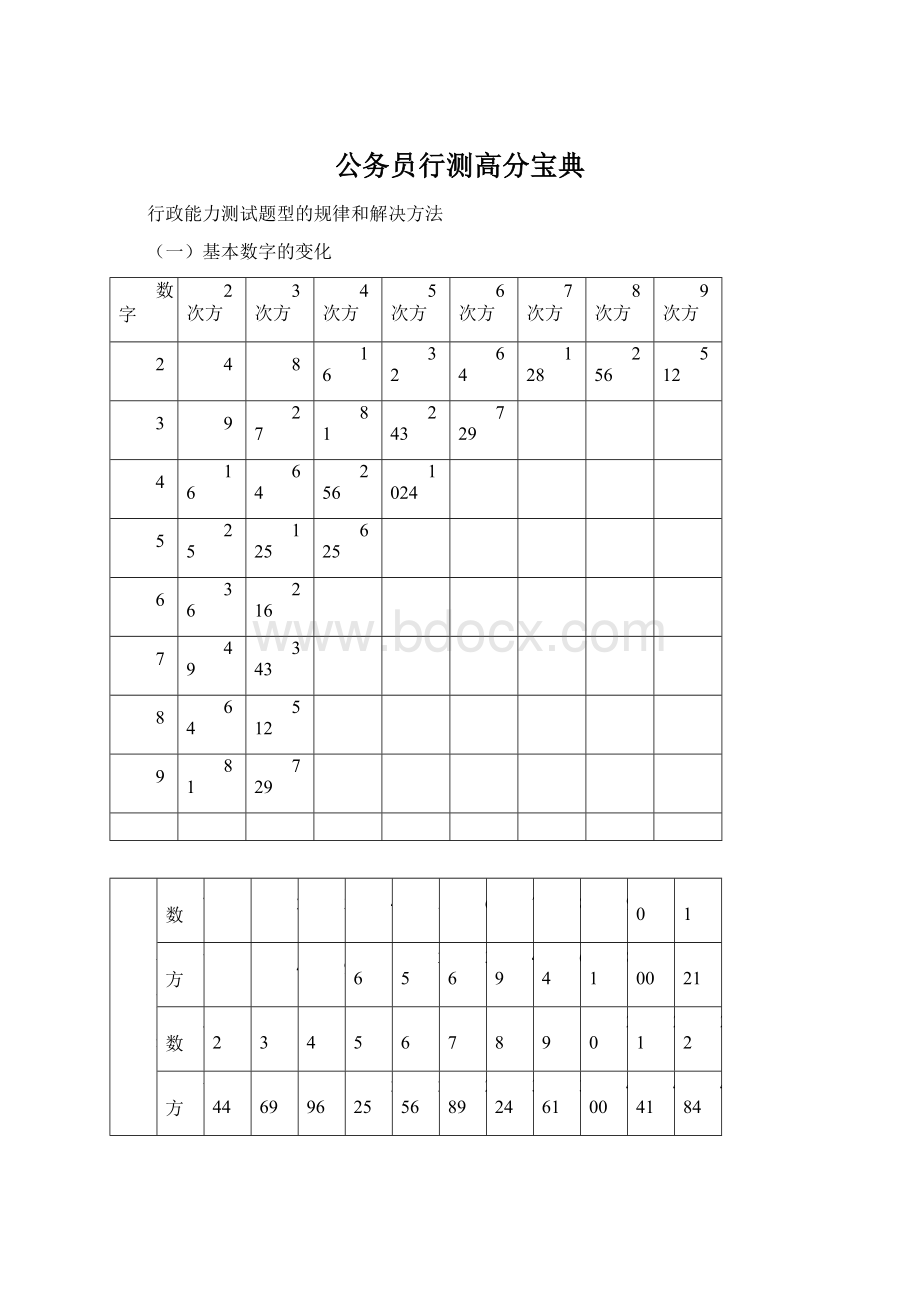
（一）基本数字的变化

数字

2次方

3次方

4次方

5次方

6次方

7次方

8次方

9次方

2

4

8

16

32

64

128

256

512

3

9

27

81

243

729

4

16

64

256

1024

5

25

125

625

6

36

216

7

49

343

8

64

512

9

81

729

平

方

数

底数

1

2

3

4

5

6

7

8

9

10

11

平方

1

4

9

16

25

36

49

64

81

100

121

底数

12

13

14

15

16

17

18

19

20

21

22

平方

144

169

196

225

256

289

324

361

400

441

484

底数

23

24

25

26

27

28

29

30

31

32

33

平方

529

576

625

676

729

784

841

900

961

1024

1089

立

方

数

底数

1

2

3

4

5

6

7

8

9

10

11

立方

1

8

27

64

125

216

343

512

729

1000

1331

多

次

方

数

次方

1

2

3

4

5

6

7

8

9

10

11

2

2

4

8

16

32

64

128

256

512

1024

2048

3

3

9

27

81

243

729

4

4

16

64

256

1024

5

5

25

125

625

3125

6

6

36

216

1296

7776

数目较大的数字没有在空格中标出，因为数字推理中涉及的数字不会特别大。

（二）基本数列的表现形式

数列名称数列构成元素描述数列形式

自然数列　略1，2，3，4，5，6，…

偶数数列　偶数：

整数中，能被2整除的数2，4，6，8，10，12，…

奇数数列　奇数：

整数中，不能被2整除的数1，3，5，7，9，11，…

质数数列　质数：

只有1和其本身两个约数2，3，5，7，11，13，…

（考试中出现的机率大）

合数数列　合数：

除了1和它本身之外还有其他的约数的数4，6，8，9，10，12，…

平方数列　略1，4，9，16，25，36，…

立方数列　略1，8，27，64，125，216，…

（三）四个特征包含：

长列，特征为“7项以上”，口诀为“交叉组合三项和”；

分数列，特征为“含分数项”，口诀为“分数多拆分通分，分数少负次相除”；

次幂列，特征为“含次幂数”，口诀为“常见数敏感，通常考修正”；

质数列与合数列，特征为“由质数或合数组成”。

（四）相邻关系包括：

相邻两项的差，相邻两项的除，相邻两项的和（和数列），以及相邻两项的积（积数列）。

二、数列命题规律总结

数字推理主要是通过加、减、乘、除、平方、开方等方法来寻找数列中各个数字之间的规律，从而得出最后的答案。

在实际解题过程中，根据相邻数之间的关系分为两大类规律：

（一）相邻数之间通过加、减、乘、除、平方、开方等方式发生联系，产生规律，主要有以下几种规律：

1.相邻两个数加、减、乘、除等于第三个数

2.相邻两个数加、减、乘、除后再加或者减一个常数等于第三个数

3.等差数列：

数列中数字相减差为一个常数或为一组循环的常数

4.二级等差：

数列中相邻两个数相减后的差值成等差数列

5.等比数列：

数列中相邻两个数的比值相等

6.二级等比：

数列中相邻两个数相减后的差值成等比数列

7.前一个数的平方等于第二个数

8.前一个数的平方再加或者减一个常数等于第二个数

9.前一个数乘一个倍数加减一个常数等于第二个数

10.隔项数列：

数列相隔两项呈现一定规律

11.全奇、全偶数列

12.排序数列

（二）数列中每一个数字本身构成特点形成各个数字之间的规律。

1.数列中每一个数字都是n的平方构成或者是n的平方加减一个常数构成，或者是n的平方加减n构成。

2.每一个数字都是n的立方构成或者是n的立方加减一个常数构成，或者是n的立方加减n构成。

3.数列中每一个数字都是n的倍数加减一个常数。

第二节题型透视与多维解题法

数项分类法：

第一类：

数项在五项以上的

1、隔项数列或分组数列

一般情况下，数项在五项以上多为隔项数列或分组数列。

2、非隔项或分组数列的

如果不是隔项数列，那么从数字的相邻关系入手，看数列中相邻数字在加减乘除后符合上述的哪种规律，然后得出答案。

第二类：

数项在五项以下的

寻找数列中每一个数字在构成上的特点，寻找规律

数项变化分析法：

1、数列中的数项呈变化幅度不大，依次递增或递减

这一类的数列多为等差、等比、和数列

2、数列中的数项变化幅度大

这一类的数列多为幂数列、积数列

这里所介绍的是数字推理的总体规律，下面针对各种题型我给大家讲解规律和技巧。

数字推理题型与口诀

数字推理的总口诀是：

先看4个特征，再做4个相邻关系，最后考虑4个三项关系。

4个特征包含：

长列，特征为“7项以上”，口诀为“交叉组合三项和”；

分数列，特征为“含分数项”，口诀为“分数多拆分通分，分数少负次相除”；

次幂列，特征为“含次幂数”，口诀为“常见数敏感，通常考修正”；

质数列与合数列，特征为“由质数或合数组成”

4个相邻关系包括：

相邻两项的差，相邻两项的除，相邻两项的和（和数列），以及相邻两项的积（积数列）。

运算递推数列

数列的规律就是从第三项开始，每项都等于它的前面两项之和

在公务员考试中，对于运算递推数列的变形应用是多种多样的。

 一、把运算递推规律改成减法

【例题1】

25，15，10，5，5，（   ）

A.10    B.5    C.0    D.－5

【解析】

本题的数列规律是第一项减去第二项得到第三项。

即：

25－15＝10，15－10＝5，10－5＝5

按照这个规律，（ ）内的数应该是5－5＝0。

所以，正确选项是C。

 二、把运算递推规律改成乘法

【例题2】

3，4，6，12，36，（   ）

A.8    B.72    C.108    D.216

【解析】

本题的数列规律是前两项的乘积除以2得到后一项。

即：

（3×4）÷2＝6，（4×6）÷2＝12，（6×12）÷2＝36

按照这个规律，（ ）内的数应该是（12×36）÷2＝216。

所以，正确选项是D。

 三、把运算递推规律综合运用

【例题3】

1，3，4，1，9（　）

A.５       B.11       C.14       D.64

【解析】

本题的数列规律是前两项差的平方得到后一项。

即：

（1－3）2＝4，（3－4）2＝1，（4－1）2＝9

按照这个规律，（ ）内的数应该是（9－1）2＝64。

所以，正确选项为D。

 运算递推数列的变式虽然有很多，但是其变形主要有两种方法：

一是运算规律的变化，把单一的加法运算变成减法、乘法、除法、乘方，或者是这些运算的混合运算；二是添加了常数项，比如上面的例题2，在乘法运算之后又添加了除以“2”这个常数项的运算。

随机组合数列

各种数列关系两两组合，甚至三种关系组合

 【例题1】

1，1，3，7，17，41（ ）

A.89       B.99       C.109       D.119

【解析】

本题考查积数列与和数列的组合。

在题干中，任意三个相邻的项，右侧项等于中间项乘以2，然后再加上左侧项。

按照这个规律，（ ）内的数应该是（41×2）＋17＝99。

所以，正确选项为B。

 【例题2】

6，15，35，77，（ ）

A．106       B.117       C.136       D163

【解析】

本题考查“斐波纳契数列”的变式与等比数列的组合。

在题干中，从左到右两个相邻项的右项等于左项乘以2，并依次加上等比数列3，5，7。

按照这个规律，（ ）内的数应该是（77×2）＋9＝163。

所以，正确选项为D。

 【例题3】

0，6，24，60，120，（）

A．186       B.210       C.220       D.226

【解析】

本题考查立方数列与项数关系的组合。

在题干中，13－1＝0，23－2＝6，33－3＝24，43－4＝60，53－5＝120。

按照这个规律，（ ）内的数应该是63－6＝210。

所以，正确选项为B。

 【例题4】

2，12，36，80，（ ）

A．100       B.125       C.150       D.175

【解析】

本题考查三级数列的组合应用。

第一步，数列每一项除以项数n，2/1＝2，12/2＝6，36/3＝12，80/4＝20，得到一个新的二级数列：

2，6，12，20。

第二步，把新二级数列的相邻项的后项减前项，得到一个简单的三级等差数列：

4，6，8，可知它的下一项为10。

第三步，还原得到数列为：

2，6，12，20，30。

二次还原可得：

2×1＝2，6×2＝12，12×3＝36，20×4＝80，30×5＝150。

按照这个规律，（ ）内的数应该是30×5＝150。

所以，正确选项为C。

 【例题5】

0，9，26，65，124，（ ）

A.165       B.193       C.217       D.239

【解析】

本题的数列规律是：

从左到右，奇、偶数项分别为自然数数列的立方再减1、加1，即：

第一项：

0＝13－1

第二项：

9＝23＋1

第三项：

26＝33－1

第四项：

65＝43＋1

第五项：

124＝53－1

按照这个规律，（ ）内的数应该是63＋1＝217。

所以，正确选项为C。

 【例题6】

0，2，10，30，（ ）

A.68       B.74       C.60       D.70

【解析】

本题的数列规律是：

第一项：

0＝（1－1）3＋（1－1）

第二项：

2＝（2－1）3＋（2－1）

第三项：

10＝（3－1）3＋（3－1）

第四项：

30＝（4－1）3＋（4－1）

按照这个规律，（ ）内的数应该是：

（5－1）3＋（5－1）＝68。

所以，正确选项为A

（一）等差数列

知识要点提示：

数列中从第2项起，每一项与它的前一项的差等于同一个常数，这个常数叫做等差数列的公差，整个数字序列依次递增或递减，等差数列是数字推理测验中排列数字的常见规律之一。

公式：

an=an-1+d，n≥2（d为公差）

解题技巧一：

邻项相减法

数列中相邻两项相减差为一个常数或一组循环的常数。

【例题】1，4，7，（）

A.8　　B.9　　C.10　　D.11

解析：

后一项减去前一项差为常数3

答案为C。

相邻两个数字之间的差是一个常数3，所以括号中的数字