完整版概率论基本公式.docx
《完整版概率论基本公式.docx》由会员分享,可在线阅读,更多相关《完整版概率论基本公式.docx(17页珍藏版)》请在冰豆网上搜索。
完整版概率论基本公式
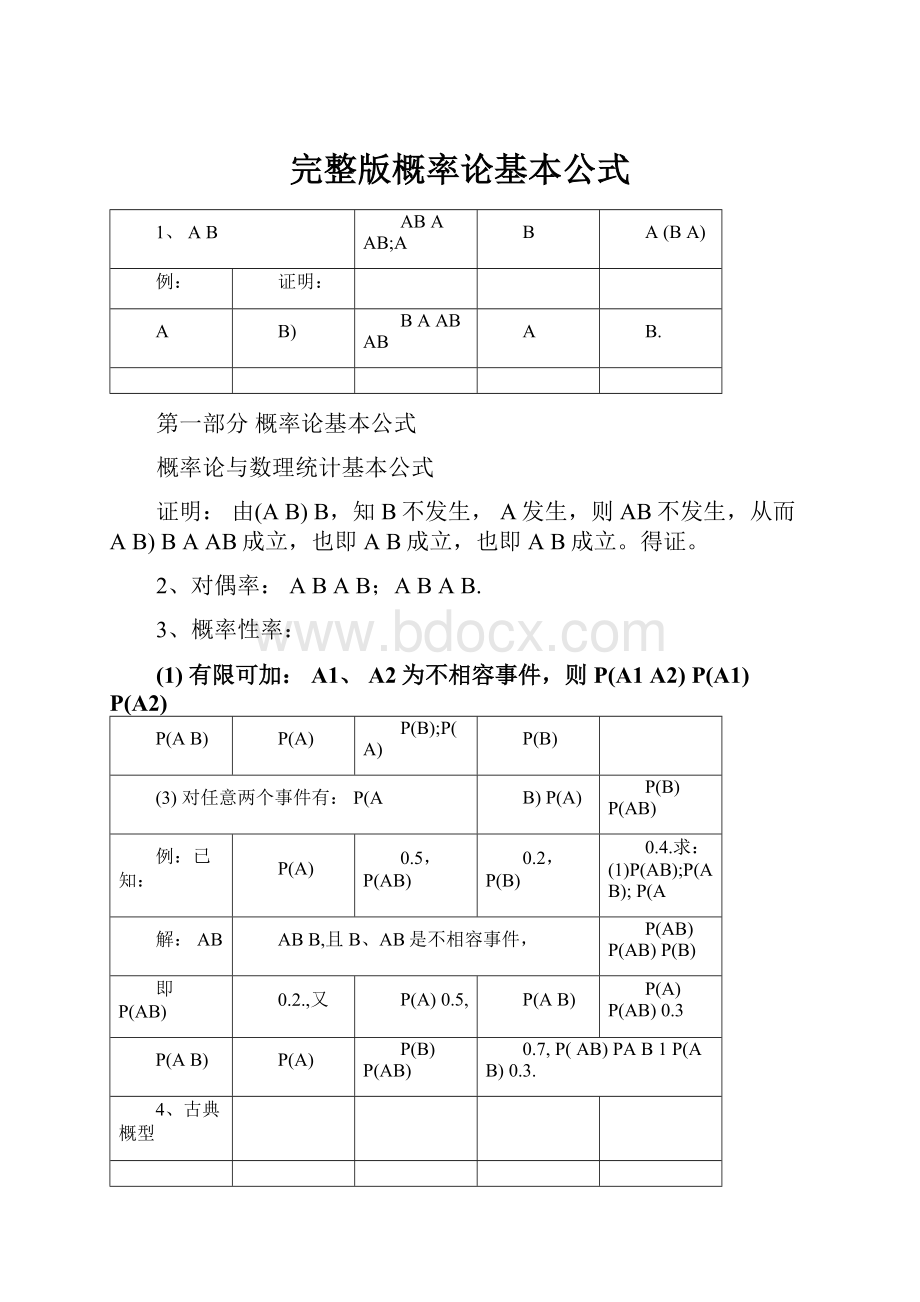
1、AB
ABAAB;A
B
A(BA)
例:
证明:
A
B)
BAABAB
A
B.
第一部分概率论基本公式
概率论与数理统计基本公式
证明:
由(AB)B,知B不发生,A发生,则AB不发生,从而AB)BAAB成立,也即AB成立,也即AB成立。
得证。
2、对偶率:
ABAB;ABAB.
3、概率性率:
(1)有限可加:
A1、A2为不相容事件,则P(A1A2)P(A1)P(A2)
P(AB)
P(A)
P(B);P(A)
P(B)
(3)对任意两个事件有:
P(A
B)P(A)
P(B)P(AB)
例:
已知:
P(A)
0.5,P(AB)
0.2,P(B)
0.4.求:
(1)P(AB);P(AB);P(A
解:
AB
ABB,且B、AB是不相容事件,
P(AB)P(AB)P(B)
即P(AB)
0.2.,又
P(A)0.5,
P(AB)
P(A)P(AB)0.3
P(AB)
P(A)
P(B)P(AB)
0.7,P(AB)PAB1P(AB)0.3.
4、古典概型
P(AB)P(A)P(AB),特别,BA时有:
(2)
B);P(AB)
例:
n双鞋总共2n只,分为n堆,每堆为2只,事件A每堆自成一双鞋的概率
2n(2-n2))!
!
2!
自成一双为:
n!
C22n
解:
分堆法:
C22n
n!
,则P(A)
5、条件概率
P(B|A)
P(AB),称为在事件A条件下,事件B的条件概率,
P(A)
P(B)称为无条件概率。
乘法公式:
P(AB)P(A)P(B|A)P(AB)P(B)P(A|B)
全概率公式:
P(B)P(Ai)P(B|Ai)
i
贝叶斯公式:
P(Ai|B)P(AiB)P(Ai)P(B|Ai)
iP(B)P(Aj)P(B|Aj)
j
例:
有三个罐子,1号装有2红1黑共3个球,2号装有3红1黑4个球,3号装有2红2
黑4个球,某人随机从其中一罐,再从该罐中任取一个球,
(1)求取得红球的概率;
(2)如
果取得是红球,那么是从第一个罐中取出的概率为多少?
解:
(1)设Bi{球取自i号罐},i1,2,3。
A{取得是红球},由题知B1、B2、B3是一个完备事件
231由全概率公式P(B)P(Ai)P(B|Ai),依题意,有:
P(A|B1);P(A|B2);P(A|B3).
i3421
P(B1)P(B2)P(B3),P(A)0.639.
3
(2)由贝叶斯公式:
P(B1|A)P(A|B1)P(B1)0.348.
1P(A)
6、独立事件
(1)P(AB)=P(A)P(B),则称A、B独立。
(2)伯努利概型如果随机试验只有两种可能结果:
事件A发生或事件A不发生,则称为伯努利试验,即:
P(A)=p,P(A)1pq(0伯努利定理:
b(k;n,p)Cnkpk(1p)nk(k=0,1,2⋯⋯)
事件A首次发生概率为:
p(1p)k1
例:
设事件A在每一次试验中发生的概率为0.3,当A发生不少于3次时,指示灯发出信号
(1)进行5次重复独立试验,求指示灯发出信号的概率;
(2)进行了7次重复独立试验,求指示灯发出信号的概率。
解:
(1)设B“5次独立试验发出指示信号”,则由题意有:
5
P(B)C5kpk(1p)5k,代入数据得:
P(B)0.163
i3
(2)设C“7次独立试验发出指示信号”,则由题意有:
7
P(C)C7kpk(1
i3
7k
p)7k1
2
C7kpk(1p)nk,代入数据,得:
P(C)0.353i0
第二章
7、常用离散型分布
(1)两点分布:
若一个随机变量
X只有两个可能的取值,且其分布为
:
P{Xx1}p;P{X
x2}1
p(0处参数为p的两点分布。
特别地,若X服从x1
1,x2
0处参数为p的两点分布,即:
X
0
1
pi
q
p
则称X服从参数为0—1分布。
其中期望E(X)=p,D(X)=p(1-p)
2)二项分布:
若一个随机变量X的概率分布由P{Xk}Cnkpk(1-p)nk
(k=0,1,2⋯⋯)
给出,则称X服从参数为n,p
的二项分布,
记为:
X~b(n,p)(
或B(n,p)
n其中P{Xk0
k}1,当n=1时变为:
P{X
k}pk(1
1k
p)1k
(k=0,1)
此时为0—1
分布。
其期望E(X)
=np,方差D(X)=n(1-p)
(3)泊松分布:
若一个随机变量X概率分布为:
P{Xk}
e
k
0,
k0,1,2
k!
则称X服从参数为的泊松分布,记为:
X~P()(或X~(),其中P{Xk}1,k0
称为泊松流强度。
泊松定理:
在n重伯努利试验中,事件A在每次试验中发生的概率为Pn,如果n时,
nPn(0的常数),则对任意给定的k,
k
有limb(k;n,p)limCnkpnk(1pn)nke,这表明,当n很大时,p接近0或1nnk!
k
时,有Cnkpnk(1pn)nke(np)。
k!
其期望方差相等,即:
E(X)=D(X)=。
8、常用连续型分布
11其期望E(X)=,方差D(X)=2.
其期望E(X)=μ,D(X)=2。
定Y的概率分布。
2)连续型随机变量函数分布方法:
设已知X的分布函数FX(x)或者概率密度fX(x),则
布函数FY(y),求出Y的密度函数。
YX21的分布函数和密度函数
解:
设FY(y)和fY(y)分别是随机变量Y的分布函数和概率密度函数,则由1x1得:
1y
2,那么当y1时FY(y)
P{Y
y}
P{X21y}
P()0,当1y
2时,得:
2
y1
0(1x)dx
Y(y)
P{Yy}P{X21
y}P{
y
1xy1
y1(1|x|)dx
y1
y1
1
y1(1
0
x)dx2y1(y
1),当y
2时,
FY(y)P{Y
y}P{X21
y}0dx
0,y1
1(1
|x|)dx1
0dx
1,所以,FY(y)
2y1
(y1),1y2,
1,y2
1
1,1y2
fX(x)
FY(y)'
y
1
0,其他
10、
设随机
变量
2
X~N(,2)
Y=aX
b也服从正态分布.即
YaXb~N(ab,(a)2)。
11、联合概率分布
(1)离散型联合分布:
Pij1
ij
XY
y1⋯⋯
yj
P{X=xi}
x1
p11
p1j
P1jj
xi
Pi1
Pij
Pijijj
P{Y=yj}
Pi1i
Piji
1
(2)连续型随机变量函数的分布:
0,其他
求f(x),f(y),E(X),E(Y),cov(X,Y),XY,D(X+Y).
0
或x>2时,由fX(x)0dy0dy0,所以,
1/8x21/4x,0x2
0,其他
2
②E(X)=xfX(x)dx7/6,由对称性同理可求得,E(Y)=7/6。
0
22
1/8xy(xy)dxdy4/3.
00
22
③因为E(XY)=xyf(x,y)dxdy
00
2
所以,cov(X,Y)=E(XY)-E(X)E(Y)=4/3-(7/6)2=-1/36。
⑤D(X+Y)=D(X)+D(Y)+2cov(X,Y)=
X的条件分布函数
边缘分布概率为FX(x)、FY(y),若对于任意x、y有:
P{Xx,Yy}P{Xx}P{Yy},即:
F(x,y)FX(x)FY(y),则称X和Y独立。
14、连续型随机变量的条件密度函数:
设二维连续型随机变量(X,Y)的概率密度为f(x,y),边缘概率密度函数为fX(x)、fY(y),则对于一切使fX(x)>0的x,定义在X=x的条件下Y的条件密度函数为:
fY|X(y|x)f(x,y),同理得到定义在Y=y条件下X的条件概率密fX(x)
度函数为:
X|Y(x|y)f(x,y),若f(x,y)=fX(x)fY(y)几乎处处成立,则称X,Y相互fY(y)
独立。
例:
设二维随机变量(X,Y)的概率密度函数为
f(x,y)
ce(2xy),x0,y0
0,其它,求
(1)确定常数c;
(2)X,Y的边缘概率密
度函数;(3)联合分布函数F(x,y);(4)P{Y≤X};
(5)条件概率密度函数fX|Y(x|y);(6)P{X<2|Y<1}
数学期望的性质:
①
变量都有数学期望。
E(CX)=CE(X)①E(X1X2)E(X1)E(X2)③设X,Y独立,
15个房间,每个房间容纳的人数不限,设X表示有人的房间数,求)
则E(XY)=E(X)E(Y).例:
10个人随机进入E(X)(设每个人进入房间是等可能的,且各人是否进入房间相互独立附:
二项分布b(n,p)和两点分布b(1,p)的另一个关系,仍设一个实验只有两个结果:
A和A,
1,第i次试验A出现
0,第i次试验A不出现
且P(A)=p,现在将试验独立进行n次,记为n次试验中结果A出现的次数,则X~b(n,p),若记Xi为第i次试验中结果A出现的次数,即:
Xi
1,第i号房间有人;
i1,2,3,
0,第i号房间没人;i1,2,3,
2
(2)方差性质:
①D(CX)=C2D(X);②若X.Y相互独立,则:
D(XY)D(X)D(Y)
17、协方差:
(1)cov(X,Y)=E(XY)-E(X)E(Y),特别,X,Y独立时,有:
cov(X,Y)=0.
(2)协方差性质:
①cov(X,X)=D(X);②cov(aX,bY)=abcov(X,Y);③cov(C,Y)=0;④cov(X1X2,Y)=cov(X1,Y)cov(X2,Y)⑤随机变量和的方差与协方差的关系
D(XY)D(X)D(Y)2cov(X,Y).
(3)相关系数XYcov(X,Y),性质:
①|XY|1;②若X和Y相互独立,则XY=0,
XYD(X)D(Y)XYXY
即X和Y不相关。
③若D(X)>0,D(Y)>0,则当且仅当存在常数a,b(a0),使:
P{YaXb}1时,|XY|1,而且a0时,XY1;当a0时,XY1.
2
④设e=E[Y-(aXb)]2,称为用aXb来近似Y的均方差,则:
设D(X)>0,D(Y)>0,有:
2
2,则对于给定任意正数
a0coDv((XX,)Y),b0E(Y)a0E(X),使均方误差达到最小。
18、切比雪夫不等式:
设随机变量X的期望E(X)=μ,方差D(X)=
2
19、大数定理:
设随机变量X1,X2,⋯⋯Xn⋯⋯相互独立,且具有相同的期望和方差:
E(Xi)
D(Xi)2,i=1,2,3⋯⋯,记Yn1Xi,则对于任意>0,有:
ni1
linmP{|Yn|}1,推论linmP{|nnA
nnnA发生的次数,p为概率。
p|
1(其中nA为n重伯努利中
20、中
心极限定理;
(1)设随机变量X1,X
2,
相互独立,服从同一分布,且
E(Xi),D(Xi)
i=1,2,3⋯⋯,则:
n
XinlinmP{n
x}
1et/2dt.一个结论:
2
n
Xi~N(0,1)/n
i1
(2)棣莫佛—拉普拉斯定理:
设随机变量X1,X2,
Xn
相互独立,并且都服从参数为p
的两点分布,则对任意实数
n
Xinpx,有:
lnimP{np(1p)
的信息,因此,当方
第二部分数理统计
21、由于样本方差(或样本标准差)很好的反应总体方差(或标准差)
差2未知时,常用S2去估计,而总体标准差
则常用样本标准差S去估计。
22、常用统计分布
(1)分位数:
设随机变量
(01),若实数F满足P{XF}
若实数T、2满足P{|X|T、2},则称T、2为随机变量X分布的的双侧分位数。
X的分布函数F(x),对给定的实数
则称F为随机变量X分布的水平的上侧分位数,
2)2分布:
设X1,X2,Xn是取自总体N(0,1)的样本,
2X12X22Xn2服从自由度为n的2分布。
E(
称统计量
2)n,D
(2)
2n,
3)t分布X~N(0,1),Y~2(n),且X和Y相互独立,则称T
Y/n
服从自由度为n的t分布。
4)F分布:
设X~2(m),Y~2(n),且X与Y相互独立,则称F服从自由度为(m,n)的F分布,记:
F~F(m,n)
X/mnX
Y/nmY22、
抽样分布A、单正态总体抽样分布
(1)设总体X~N(,2),X1,X,2,Xn是取自X的一个样本,
X为该样本的样本均值,则有:
X~N
2X
2/n);UX~N(0,1)
/n
B、双正态总体抽样分布:
是总体分布的未知参数,为估计未知参数,需要构造一个适当的:
(X1,X2,Xn),然后观察值:
(x1,x2,xn)来估计,(X1,X2,Xn)称为
的估计量,(x1,x2,xn)称为的估计值,估计量和估计值统称为点估计。
设(X1,X2,Xn)是未知参数的估计量,若E(),则称为的无偏估计量,
设X1,X,2,Xn是取自X的样本,总体X的均值为,方差为2,则:
样本均值X是的无偏估计量,样本方差S2是2的无偏估计量,样本二阶中心矩1n
1(XiX)2是2的无偏估计量。
ni1
24、点估计常用方法
(1)矩估计法:
先求E(X),得到一个E(X)与未知参数的式子,用E(X)表示未知参数,再把E(X)用X代替即可。
例:
已知总体X的概率分布为P{Xk}C2k
(1)k2k,k0,1,2,求参数的矩估计。
1-E(X)
2
n
解:
E(X)xiP{Xk}0x21x(21-)(21-)22-2,
i1
用样本均值X代替E(X)得到的矩估计为:
1-X。
(2)最大似然估计:
一般方法:
a、写出最大似然函数
L(x1,x2,xn;);b令dL()0或dlnL()0,求出驻点;c、判断并求出最大
dd值点,在最大值点得表达式中,用样本均值代入即得到参数的最大释然估计值。
并在原假设H0成立的前提下导出U的概率分布,要求U的分布不依赖于任何未知参数;
(4)确定拒绝域,即依据直观分析先确定拒绝域形式,然后根据给定的显著性水平α和U
的分布,由P{拒绝H0|H0为真}=α,确定拒绝域的临界值,从而确定拒绝域W;(5)做一
次具体抽样,根据得到的样本观察值和所得的拒绝域,对假设H0做出拒绝或接受的判断。
例:
水泥厂用包装机包装水泥,每袋额定重量50千克,某日开工后随机抽查了9袋,得其样本均值为49.9,样本方差为0.29.假设每袋重量服从正态分布,问包装机工作是否正常(0.05)?
(已知t0.025(8)2.306)
解:
(1)建立假设H0:
μ=50,H1:
μ≠50;
2)选择统计量:
T(X0)/(S/n)~t(n1);
3)对于给定的显著性水平α,确定k,使
P{|T|>k}=α,查t分布表得:
kt/2t0.025(8)2.306,从而
得拒绝域为:
|t|>2.306.
即认为包装正常