深基坑钢板桩支护计算.docx
《深基坑钢板桩支护计算.docx》由会员分享,可在线阅读,更多相关《深基坑钢板桩支护计算.docx(16页珍藏版)》请在冰豆网上搜索。
深基坑钢板桩支护计算
1、工程简介
越南沿海火力发电厂3期连接井位于电厂厂区内,距东边的煤灰堆场约100m,连接井最南侧距海边约30m~40m。
现根据施工需要,将连接井及部分陆域段钢管段设置成干施工区域,即将全部连接井及部分陆域钢管段区域逐层开挖成深基坑,然后在基坑进行施工工作。
基层四周采用CDM桩或者钢板桩进行支护。
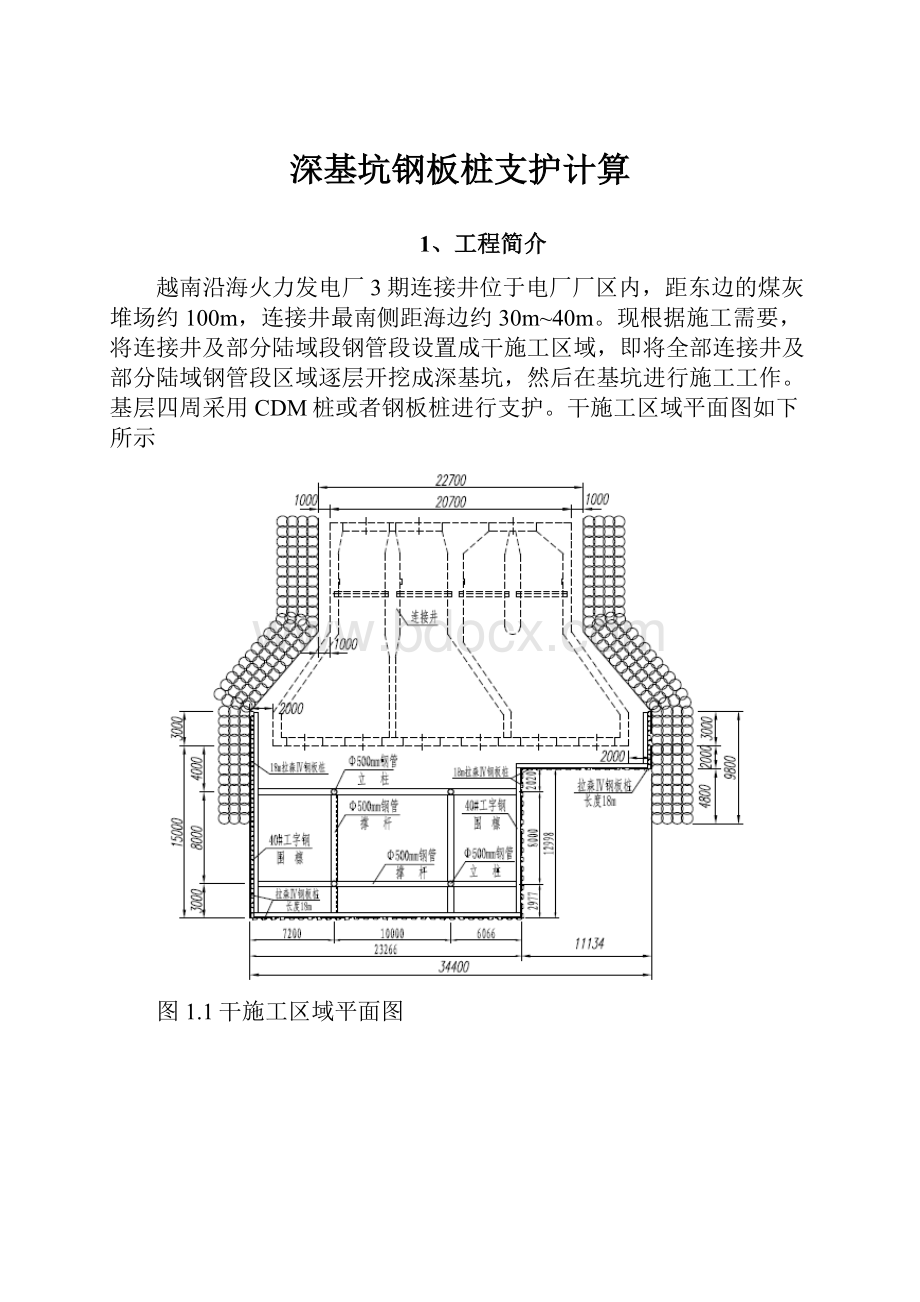
干施工区域平面图如下所示
图1.1干施工区域平面图
图1.2基坑支护典型断面图(供参考)
2、设计资料
1、钢板桩桩顶高程为+3.3m;
2、地面标高为+2.5m,开挖面标高-5.9m,开挖深度8.4m,钢板桩底标高-14.7m。
3、坑内外土体的天然容重γ为16.5KN/m2,内摩擦角为Φ=8.5度,粘聚力c=10KPa;
4、地面超载q:
按20KN/m2考虑;
5、钢板桩暂设拉森Ⅳ400×170U型钢板桩,W=2270cm3,[δ]=200MPa,桩长18m。
3内力计算
3.1支撑层数及间距
按等弯矩布置确定各层支撑的间距,则钢板桩顶部悬臂端的最大允许跨度为:
h1=1.11h=1.11×2.603m=2.89m
h2=0.88h=0.88×2.603m=2.29m
根据现场施工需要和工程经济性,确定采用两层支撑,第一层h=1.2m,支撑标高+1.3m;第二层支撑h1=2m,支撑标高-0.7m。
3.2作用在钢板桩上的土压力强度及压力分布
主动土压力系数Ka=tan²(45°-φ/2)=tan²(45°-8.5°/2)=0.742
被动土压力系数Kp=tan²(45°+φ/2)=tan2(45°+8.5°/2)=1.347
工况一:
安装第一层支撑后,基坑内土体开挖至-0.7m(第二层支撑标高)。
1、主动土压力:
①z=0mPa=20×0.742+16.5×0×0.742=14.84KN/m2
②z=3.2m(地面到基坑底距离))
Pa=20×0.742+16.5×3.2×0.742=54.02KN/m2
2、被动土压力:
①z=3.2m(地面到基坑底距离)
Pp=16.5×(3.2-3.2)×1.347=0KN/m2
②z=17.2m(地面到钢板桩底距离)
Pp=16.5×(17.2-3.2)×1.347=311.157KN/m2
3、计算反弯点位置:
假定钢板桩上土压力为零的点为反弯点,则有:
Pa=Pp
Pa=20×0.742+16.5×z×0.742=Pp=16.5×(z-3.2)×1.347
z=8.61m
4、等值梁法计算内力:
钢板桩AD段简化为连续简支梁,用力矩分配法计算各支点和跨中的弯矩,从中求出最大弯矩Mmax,以验算钢板桩截面;并求出各支点反力Rb、Rd,Rb即为作用在第一层支撑上的荷载。
图1.3等值梁计算图式
求得:
Rb=173.81KN/m;(即第一层围檁每米受力173.81KN/m)
Rd=82.48KN/m;
工况二:
安装第二层支撑后,基坑开挖至-5.9m。
1、主动土压力:
①z=0mPa=20×0.742+16.5×0×0.742=14.84KN/m2
②z=8.4mPa=20×0.742+16.5×8.4×0.742=117.7KN/m2
③z=17.2mPa=20×0.742+16.5×17.2×0.742=225.4KN/m2
2、被动土压力:
①z=8.4mPp=γzKp=16.5×(8.4-8.4)×1.347=0KN/m2
②z=17.2mPp=γzKp=16.5×(17.2-8.4)×1.347=195.6KN/m2
3、计算反弯点:
Pa=Pp
假定钢板桩上土压力为零的点为反弯点,则有:
Pa=Pp
Pa=20×0.742+16.5×z×0.742=Pp=16.5×(z-8.4)×1.347
求得:
z=20.19m
4、等值梁法计算内力
钢板桩AE段简化为连续简支梁,用力矩分配法计算各支点和跨中的弯矩,从中求出最大弯矩Mmax,以验算钢板桩截面;并求出各支点反力Rb、Rc、Re,Rb、Rc即为作用在第一层、第二层支撑上的荷载。
图1.3等值梁计算图式
求得:
Rb=-3286KN/m;
Rc=4474.94KN/m;
图1.4钢板桩受力图
3.3计算钢板桩最小入土深度
钢板桩入土深度主要受两个因素的影响,一是竖向不产生管涌,二是基底土体横向不产生侧移。
按工况二考虑,以土体侧向稳定性来分析:
最小入土深度t=1.1(y+x)=1.1×(0+51.86)=57.046m
实际入土深度8.8m<57.046m,不满足规范要求。
基坑底部土体会发生横向侧移。
4、稳定性验算
4.1抗倾覆稳定性验算
1、从第二层支撑以下外侧主动土压力对支撑点的力矩:
MQC=(54.02+225.4)×14÷2×14×2/3=18255.44
2、内侧被动土压力对第二层支撑点的力矩:
MRC=195.6×8.8÷2×(5.2+8.8×2/3)=9524.416
3、抗倾覆稳定性安全系数
KQ=MRC/MQC=19048.332÷18255.44≈0.52<1.05
不符合规范要求。
4.2基底抗隆起稳定性分析:
地基承载力系数:
Nq=eπtgφtg2(45+φ/2)=eπtg8.5tg2(45+8.5/2)=2.153
Nc=(Nq-1)÷(tgφ)=(2.153-1)÷(tg8.5)=7.715
抗隆起安全系数
不满足要求,基坑底部土体会发生隆起。
附录
上述的计算都是遵循下述的公式
1、土压力
支护结构承受的土压力,与土层地质条件、地下水状况、支护结构构件的刚度亦即施工工况、方法、质量等因素密切相关。
由于这些因素千变万化,十分复杂,因此难于计算土压力的准确值。
目前国内、外常用的计算土压力方法仍以库仑公式或郎肯公式为基本计算公式。
库仑公式和郎肯公式均为假设土体为极限平衡状态下的计算公式。
1、主动土压力强度
①无粘性土
②粘性土
式中:
γ——土的容重
c、Φ——分别为土的粘聚力、内摩擦角
z——计算点处土体深度
Ka——郎肯主动土压力系数
2、被动土压力强度
①无粘性土
②粘性土
式中:
γ——土的容重
c、Φ——分别为土的粘聚力、内摩擦角
z——计算点处土体深度
Kp——郎肯被动土压力系数
2、多撑(多锚)式钢板桩计算
2.1支撑(锚杆)的布置和计算
支撑(锚杆)层数和间距的布置,影响着钢板桩、支撑、围檩的截面尺寸和支护结构的材料量,其布置方式有以下两种:
1、等弯矩布置
这种布置是将支撑布置成使钢板桩各跨度的最大弯矩相等,充分发挥钢板桩的抗弯强度,可使钢板桩材料用量最省,计算步骤为:
①根据工程的实际情况,估算一种型号的钢板桩,并查得或计算其截面模量W。
②根据其允许抵抗弯矩,计算板桩悬臂部分的最大允许跨度h。
式中,[δ]——钢板桩抗弯强度设计值;
W——截面抗弯模量;
γ——钢板桩后土的重度
Ka——主动土压力系数;
③计算板桩下部各层支撑的跨度,把板桩视作一个承受三角形荷载的连续梁,各支点近似的假定为不转动,即把每跨看作两端固定,可按一般力学计算各支点最大弯矩都等于Mmax、Mmin时各跨的跨度,其值如图3.1.3-1所示。
④如果算出的支撑层数过多或过少,可重新选择钢板桩的型号,按以上步骤进行计算。
图3.2.3-1支撑的等间距布置
2、等反力布置
这种布置是使各层围檩和支撑所受的力都相等,使支撑系统简化。
计算支撑的间距时,把板桩视作承受三角形荷载的连续梁,解之即得到各跨的跨度如图3.1.3-2所示:
图3.2.3-2支撑的等反力布置
这样除顶部支撑压力为0.15P外,其他支撑承受的压力均为P,其值按下式计算:
通常按第一跨的最大弯矩进行板桩截面的选择。
2..2多撑(多锚)式钢板桩入土深度计算
多撑(多锚)式钢板桩入土深度,可用盾恩近似法或等值梁法进行计算。
1、盾恩近似法计算
其计算步骤如下:
①绘出板桩上土压力的分布图,经简化后的土压力分布如图3.2.3-3所示。
图3.2.3-3多层支撑板桩计算简图
②假定作用在板桩FB′段上的荷载FGN′B′。
一半传至F点上,另一半由坑底土压力MB′R′承受。
由图3.2.3-3几何关系可得:
即:
式中:
Ka、Kp、H、L5均为已知,解得x值即为入土深度。
③坑底被动土压力的合力P的作用点,在离基坑底2x/3处的W点,假定此W点即为板桩入土部分的固定点,所以板桩最下面一跨的跨度为:
④假定F、W两点皆为固定端,则可近似地按两端固定计算F点的弯矩。
2、等值梁法计算
其计算步骤同单撑(单锚)板桩:
①绘出土压力分布图,如图3.2.3-4;
图3.2.3-4等值梁法计算多层支撑板桩计算简图
(a)土压力分布图;(b)等值梁;(c)入土深度计算简图
②计算板桩上土压力强度等于零点离开挖面的距离y值;
③按多跨连续梁AF,用力矩分配法计算各支点和跨中的弯矩,从中求出最大弯矩Mmax,以验算板桩截面,并可求出各支点反力RB、RC、RD、RF,即作用在支撑上的荷载。
④根据RF和墙前被动土压力对板桩底端O的力矩相等的原理可求得x值,而t0=y+x
所以板桩入土深度为:
t=(1.1~1.2)t0
3稳定性验算
3.1基坑底部土体的抗隆起稳定性验算
包括以下内容:
3.2.1.1板桩底地基承载力,按照下式计算:
结构底平面作为求极限承载力的基准面,可由以下公式求抗隆起安全系数
式中:
γ1——坑外地表至板桩底,各土层天然重度的加权平均值;
γ2——坑内开挖面以下至板桩底,各土层天然重度的加权平均值;
c——桩底处地基土粘聚力;
q——基坑外地面荷载;
h0——基坑开挖深度;
D——板桩在基坑开挖面以下的桩入土深度;
Nq、Nc——地基承载力系数;
Φ——桩底处地基土内摩擦角;
Kwz——围护墙底地基承载力安全系数,根据基坑重要性取值。
一级基坑工程取2.5;二级基坑工程取2.0;三级基坑工程取1.7。
备注:
基坑工程根据其重要性分为以下三级:
1、符合下列情况之一时,属一级基坑工程:
①支护结构作为主体结构的一部分时;
②基坑开挖深度大于、等于10米时;
③距基坑边两倍开挖深度范围内有历史文物、近代优秀建筑、重要管线等需严加保护时。
2、除一级、三级以外的均属二级基坑工程;
3、开挖深度小于7米,且周围环境无特别要求时,属三级基坑工程。
图3.3.1-1围护墙底地基承载力验算图式
3.1基坑底部土体的抗隆起稳定性
按照下式计算:
式中:
MRL——抗隆起力矩;
γ——围护墙底以上地基土各土层天然重度的加权平均值;
D——围护墙在基坑开挖面以下的入土深度;
Ka——主动土压力系数,取
;
c、Φ——滑裂面上地基土的粘聚力和内摩擦角的加权平均值;
h0——基坑开挖深度;
α1——最下一道支撑面与基坑开挖面间的水平夹角;
α2——以最下一道支撑点为圆心的滑裂面圆心角;
q——坑外地面荷载;
MSL——隆起弯矩,
;
KL——抗隆起稳定性安全系数;一级基坑工程取2.5;二级基坑工程取2.0;三级基坑工程取1.7。
图3.2.1-2基坑底抗隆起计算简图
3.2抗管涌验算
地下水位较高的地区,开挖后会形成水头差,产生渗流,当渗流较大时,有可能造成底部管涌稳定性破坏。
因此,验算管涌稳定性也是十分必要的,可通过下式对其进行验算:
式中:
ic——临界水力坡度,
ρ——坑底土体相对密度
e——坑底土体天然空隙比
i——渗流水力坡度,
hw——坑内外水头差;
L——最短渗流流线长度;
Kg——抗渗流安全系数,取1.5~2.0。
基坑底土为砂性土、砂质粉土或粘性土与粉性土中有明显薄层粉砂夹层时取最大值。
图3.3.2基坑底土体渗流计算简图
3.3抗倾覆稳定性验算
钢板桩结构的抗倾覆稳定性,可按下式验算:
式中:
MRC——抗倾覆力矩。
取基坑开挖面以下钢板桩入土部分坑内侧压力,对最下一道支撑或锚定点的力矩。
MQC——倾覆力矩。
取最下一道支撑或锚定点以下钢板桩坑外侧压力,对最下一道支撑或锚定点的力矩。
KQ——抗倾覆稳定性安全系数,一级基坑工程取1.20;二级基坑工程取1.10;三级基坑工程取1.05。
图3.3.3抗倾覆稳定计算图式
3.4变形估算
当基坑附近有建筑物和地下管线时,必须对支护进行变形估算,以确保建筑物及管线的安全,变形包括支护周围土体变形和地基回弹变形两部分,对于中小基坑地基回弹变形可不进行估算。
基坑周围土体的变形应根据土质、支护情况及当地经验采用合适的估算方法,本文采用以下公式计算:
式中:
k1——修正系数,对于钢板桩k1=1.0;
h——基坑开挖深度;
α——地表沉降量与基坑开挖深度之比(%),可参照图3.4查得;
图3.4α系数表