圆锥曲线笔记D.docx

圆锥曲线笔记D.docx

《圆锥曲线笔记D.docx》由会员分享，可在线阅读，更多相关《圆锥曲线笔记D.docx（31页珍藏版）》请在冰豆网上搜索。

圆锥曲线笔记D

D.解析圆锥曲线（上）（用解析几何研究圆锥曲线）

1.圆锥曲线的准圆

a.椭圆的内准园与外准圆

2

设椭圆的方程为笃

a

内准圆定义：

在椭圆内部存在使与其相切的椭圆的弦的中心

角都为90度称为内准圆

AB为椭圆的弦，且中心角AOB90o记AOXA

BOXB（0oA90o,0oB90o,AB90o）,AO「a,BO「bA（rAcosA,rAsinA）,B（rBcosB,rBsinB）代入椭圆的方程得到（rAcosA））（rAsinA）2.（rBcosB））

I（

2

「A

b2a2b2

2

（gsinB）.

b21

22

（asinA）（bcosA）

22

ab

22

「A「B_

2

「B

2「A

光AB到椭圆中心的距离为爲^

（asinB）2（bcosB）2

22

与1的内准圆方程为x2

ab

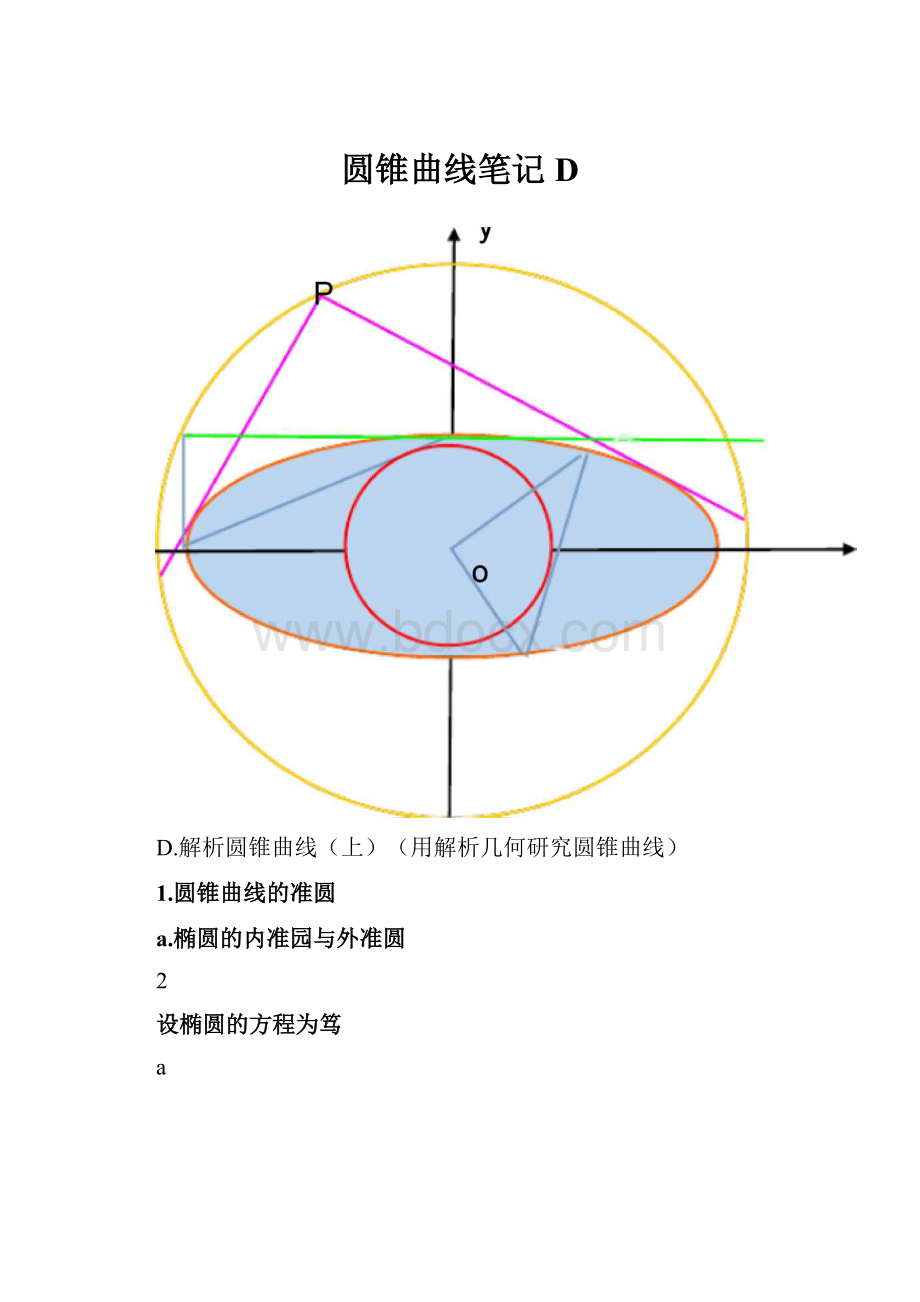
外准圆定义：

椭圆两条垂直切线交点的轨迹

如图P（x°,y°）为椭圆外的一点，且满足，过P作椭圆的两条切线相互垂直

当P点的切线斜率不存在时P点在（a，b）这四点到椭圆中心的距离都为.a^b2当斜率存在时设过P点椭圆的切线为k（xXq）yy0即kxyy0kx00代入椭圆的方程

（a2k2b2）x22a2k（y0kx0）xa2（y0kx0）2b20

又因为是切线故0

a2k2b2（y°kx）20（a2X02）k22x0y°kb2y。

20

.22

by°

-22

ax°

-1

x02y02a2b2即当斜率存在时P点到椭圆中心的距离为、a2b2

此方程即为过P两切线斜率的二次方程两斜率乘积为-1

综上椭圆的外准圆存在且方程为x2y2a2b2

b.双曲线的虚实准圆

22

设双曲线的方程为与-与1（a0,b0）

ab

虚准圆定义：

与椭圆的内准圆相似一个以双曲线的中心为圆心使与其相切的双曲线的弦的中心角为90的圆被称为双曲线的虚准圆（必须

有b>a>0,否则不存虚准圆）

设双曲线弦AB方程为y=kx+m

A（Xi,yJ,B（X2,y2）

AB方程代入双曲线的方程得

（22

（ak

b2）x

（22

（ak

b2）y

xiyi

X2y2

X2『2

2

0

所以双曲线务

a

b2）

m2）

2222

b）b（aki

22a2kmxa2（m2

22b2myb2（a2k2

2#2.2、.2“a（m

a

2

m

k21

2

卡1（b

b

丨0

2）

…2四,又AOB90o

2k2b2

2J

ab

22

ba

AB直线到双曲线的距离为

a0）的虚准圆为x2

2.2

ab

22

ba

（也可像证明椭圆内准圆一样引入三角参数）

定值—b2~a2

实准圆定义：

类似与椭圆的外准圆，双曲线两条相互垂直的

如图P（x0,y。

）为双曲线外的一点，且满足，过P作双曲线的两条切线相互垂直

0代入双曲线的方

当斜率存在时设过P点双曲线的切线为k（xx0）yy（即kxyy0

（a2k2-b2）x22a2k（y°kx0）xa2（y0kx0）2b20

又因为是切线故0

a2k2b2（yokx）20（a2x。

2）k22x°y°kb2y。

20

-b2

~2

a

2

y。

~T

Xo

-1

22

xoyo

a2-b2即P点到双曲线中心的距离为Ja2-b2

此方程即为过P两切线斜率的二次方程两斜率乘积为-1

综上双曲线的实准圆存在且方程为x2y2a2-b（ab0）

C.抛物线的准线是特殊的准圆

准确来说抛物线并没有类似于有心圆锥曲线的准圆存在，但是抛物线两条垂直的切线的交点的轨迹为其准线，可以理解为半径无大的圆

结合上节几何中的抛物线结论容易的出这一结论此处便不

再赘述（用解析法同样可以轻松得到）

2.圆锥曲线直线过定点问题

圆锥曲线的定点问题是让很多人感到头疼的问题，以至于对此类问题形成畏惧心理，观其本质其实并不复杂，主要问题是在于计算量过大，本节将介绍圆锥曲线几个典型过定点问题希望能对大家有所帮助。

对于直线过定点我们其实应该知晓其在解析几何上的表现形式，一般将直线设为斜截式y=kx+m或x=ky+n只要找出

斜率与截距的一次线性关系即可确定直线过定点，明确此节我们寻找定点也就转化成了在方程变换中找到一个关于斜率与截距的关系式（例如：

y=kx+m若有m=-3k+3则直线过

（3，3）点）

a.斜率定积

当圆锥曲线上一定点于两动点满足定点与两动点的连线的

斜率乘积（乘积不等于0,以及1-e2）为一定值时，两动点的

连线必然过定点

2

设：

椭圆方程为x2

a

2

爲1（abb2

A（x1,y1）,B（x2,y2）为椭圆上的两动点

0）P（xo,yo）为其上一定点（

（异于P点）且有kApkBp（

AB:

ykxm

代入椭圆方程:

（a2k2b2）x22a2kmxa2（m2b2）0

（a2k2b2）y22b2myb2（m2a2k2）0

2a2km

X1x222r~2，y1

akb

y2

2

2bmy

~22akb

X1X2

2（2

a（m

22

ak

b2）b2Z

.2t22|2、

b（mak）

2~22

akb

kAP

kBP

（y1y°）（y2y。

）

（X1X0）（X2X°）

2

ax0

2

l

2a

222yoab

）k2

22

2akmx02b

myob

22,2

mb

2

yo

a

X0（

2

2

2

2

2‘

“22

22

22、

.2“

a

Xo

bXo）k

amxok

（ab

bXo

am）

b（m

Xo（

2

一2

一一2

2

2.

“22

22

、.2z

、2

a

Xo

bXo）k

amxok

（am

ayo

）b（m

iyo）

Xo（

a

2

Xo

b2Xo）k2

2

a2mx0k

a（m

yo）

b2（m

yo）2

0

Xo（

a

2

Xo

b2Xo）k2

2

a2mx0k

2,2a（m

yo）

b2（m

yo）2

0

Xo（

a

2

Xo

22bXo）k

2

a2mx0k

z2

（am

2

ayo

b2yo

2

bm）（m

b2x。

2

0,

22

yo

e2）

a2b2）

b2

2

X0

（得到下式后为得出

k与m的关系，应将

k或m当作方程的主元化简

当化简遇到瓶颈时注意b2x02a2y02a2b2

0

y。

）

（kx0m

bx°）k

y。

）2

m0

y°）（a2X0

22y°by°b

22ama

（2

2b2

1.椭圆

（a2x0bx0）ka2ma2y0b2y0b2m0,（kx0my0）0（此式成立则AB过P点不符题意舍）

a2b2

yk（x—x°）

ab

2a

2a

b2

b2y0

AB过定点（

2,2

ab

2,2X0,

ab

b2

a2

b2

y°）

特别地当e21当0时没有意义

冬时AB定向但不过定点

a

b2

—2时AB过椭圆中心,a

1-e2

2.双曲线

22

设：

双曲线方程为笃-爲1（a0，-0）P（x0,y0）为其上一定点（-a-

A（x1,y1）,B（x2,y2）为双曲线上的两动点（异于P点）且有kAPkBP（

AB:

ykxm

0,

XiX2

/2.2

（ak-

-b2）

2X

2a2kmx

2/2a（m

b2）

0

（ak-

-b2）

2

y

2

2bmy-

22b（m

a2k2）

0

km

y2

2

2bmy

y1

2|2.2

代入椭圆方程:

kAPkBP

2a2

a2k2

a2（m2-2）

冇厂，y〃2

ak-

（y1『。

你

ak-

J/222

-（mak）

^~2~|_2

ak-

y。

）

（XiXo）（X2Xo）

（得到下式后为得出k与m的关系，应将k或m当作方程的主元化简）（2a2x02a2y02a2b2）k22a2kmx0

/2,22、，2小2,2

ax0-bx0）k2amx0kam

y°）（a2X0b2x°）ka2m2

2.22.2

a-ba-b打

2X0，2]2丫0）（

bab

%时AB过双曲线的中心

a

（kx0m

AB过定点

特别的当

22

X0

22

ay°

e2）

a2b2）

（a2

e21

当0时没有意义

1-e2

3•抛物线

抛物线设：

方程为设AB方程为x

2

y

2

X

ky

kAPkBP

2b2

2

.22.2222

my0-m-y0a-

222

ay0-b（my0）0

22

am

22

y。

0,

e2

-2m2-2

§）

a2

2

y。

a2m

-2X0

b2

-y时AB定向但不过定点

a

2

y

m代入抛物线方程

2px（p

0）（其余同上）（y。

22px。

）

2pky

2（pk2

2pm0

m）xm20

2

2pm2pky°y°

2

m22pk2X02mx0x02

22

y0k2py°k（x°

（ky0mx°）（y°k定点（X0红，y°）（

m）

X0

2p（X0m）0

m2p）0

e20）

附加：

圆锥曲线的共轭性质

1.直线定向

本节中证明了当斜率乘积为定值（不等于0,不等于1-e2）

对于定值等于i-e2时，有心圆锥曲线会使上节中两动点的连

线定向（斜率为定值）而不过定点。

（以椭圆为例）

下证明之（条件同上节，只是

1-e2）

2

设：

椭圆方程冷

a

且kapkbp1

22

爲i为,AB方程为ykxm,（笃ba

b2

p,A（xi,yi）,B（X2,y2）将AB方程代入曲线方程得a

z22

（ak

22

（ak

b2）x2

b2）y2

2222

2akmxa（mb）02b2myb2（m2

a2k2）0

kAPkBP

（yi

y°）（y2y。

）i

2a2kma2k2b2

2b2ma2k2b2

yo（yiy2）

Xi

yi

a2（m2b2）

X2,

222

akb

2222、

b（mak）

%x2

厂yiy2

y2，^V

~~2

a

2

yo_

2

（XiXo）（X2Xo）

a2k2）2b2myoy°2（a2k

2,2.2a2（m2b2）2a2kmX3x02（a2k2b2）a2b2（m2b2）2a2b2kmx）b2x02（a2k2a2（a2b2b2x°2a2y^）k22a2b2x02k22a2b2mx）kXo2k2mxokyo2my°

b2（m2

2

XiX2Xo（XiX2）Xo

b2）

b2

~2

a

b2）a2b2（m2

b2（b2Xo2a2b2

2a2b2mXok

2a2b2y022a2b2my00

0

2222

ak）2abmyo

2222

ayo）2abmyo0

22222、ayo（akb）

（kXoyo）（kXomy。

）

0k北直线定向

Xo

双曲线证明过程几乎一样不再赘述（也可以曲线方程为一般

的有心圆锥曲线直接证明）

2.中垂定理于圆锥曲线的推广

圆的任意一条弦中点于圆心的连线必与弦垂直，椭圆其实被压扁的圆，也该存在类似的性质，进而推广至其他圆锥曲线。

设一般圆锥曲线的方程为Ax2By22Cx2DyE0

（离心率e、A1,中心坐标O（-C，-D））

\\B\AB

A&^yJ，B（x2,y2）为圆锥曲线上异于顶点的两点AB中点为T

22

A%B%2。

捲2Dy!

E0_

则必有171171两式作差

22

Ax2By22Cx22Dy2E0

（X1

X2：

）A（x1

X2）

2C

（y1

y2）B（y1y2）2D0

y1

y2

（

2）

y1

y2

2

B）

A

e21

X1

X2

%

X2

（

C）

B

2A

KtoKabe21（当弦的极限位置变成切线是切点即变为中点同样有此性质）

22

椭圆X2y21

a2b2

22

双曲线221

ab

抛物线y22px

圆x2y2r2

bi

bl

0

-1

2a

2a

由此我们还可以得到另一性质

斜率乘积为定值中定值=i-e2不谋而合!

AB定向且Kab过p点切线的斜率0

（下以椭圆，抛物线为例以不同的方法证之

a.椭圆

2

法一：

设：

椭圆的方程为x2

a

2

y21（ab

b2

A（Xi,yJB（X2,y2），AB直线方程为y

代入椭圆方程

（a2k2

（a2k2

0）,

P（x0,y0）椭圆上一定占

'定点

kx

x1x2

x1x2

Kpa

b2）x2

b2）y22b2my

2a2km

a2k2b2，yi

a2（m2b2）

a2k2b2，yiy2

Kpb0^i^

（XiXg）

2a2kmxa2（m2b2）（

b2（m2a2k2）2b2m

~~222

akb

2/222、

b（mak）

y2

2a2b2a2k2b2

（yi

222

akb

®y。

）0

（X2y。

）

y°）（x2«）（y2y°）（xi«）0

yiX2y°（xi

・22・

x』2

222

2abk2akmy0aXyok2a2（my°

2

ay

x

X2）x°（yiy2）2x0y0

222

2bmx32x0y0（ak

b2）kb2mx0b2x0y0

b2x°

（my。

）

注意a2y2b2x‘

0

b2）

0

22,2ab

22

（ayok-bx°）（kx0my°）0b2X0

k厂

aYq

p点切线斜率的相反数

法二:

如图T,H,S分别为AP,BP,AB的中点

KapKbp0

（1）

KHO

Kto

0（KapKtoKbpKho

-）⑵

a

yi

y。

y2

y00

（1）

（2）

Xi

X。

X2

X0Xiy2

yiX2

y°（xi

X2）

y2）

2x°y°

0

11八厶丿

yi

y°y2

y0Xiy2

yiX2

y°（xi

X2）

X0（yi

y2）

2x°y°

0

xi

X0X2

X0

xiy2

yiX2

2約0

0（3）

2a2b2k

又xiy2

yx

2.2・

2（4）

akb

x0y0（a2k2b2）a2b2k

222

（ay°k-bx）（x°ky°）0

22

k警或込

ay°

X0

又由⑴

（2）

yyiy2

0（5）若Kab

yc

X0XiX2

X0

则KabKso

i而我们知道

KabKso-

■by故Kab

y

a

X0

法三：

如图P点关于椭圆对称轴的对称点为Q（x0,y0）

或

（-

X0,y0

）但是Kqo

X0

y

yi

y2

0（5）Kpo

Kso0

KsoKqo

X0

Xi

X2

b2

~2

又

a

oKab

a

k

qoK

AB

VlK

AB

b2K

2AB

b2X0

2

X0

a

ay°

-jfcw

设醮的方程拘一+等=2⑰玖叫小诙上的定点

斑七小）拘棉區1上异于戸点的两訪点且竊足匕十心二就乂#0）

谩丽方稈为&+删代入満區1方稈稈：

L椭圆

0期

（a-k：

'+b'）x2¥la1iom+（m3

（/■fc■齐4肝、£一lb2kdfMX+占4（曲，

-护）=0

n

一/P）-0

Y

当圆继曲线上一定点于两动点满足定点与两动点的连线的斜車之和

（和不等于0）为一定值时，两动点的连线必然过定点,

2

与椭圆相同经过运算（还是用韦达定理去伪存真）可以得到直线过定点（X。

少，空导y0）（0）

a

抛物线过定点（—-Py0,x022y）（0）（运算参考椭圆）

圆锥曲线中直线过定点问题还有另一种

b斜率定和

b+走肿=<=肌"恥+网-N二二=>側1%）（£-％）+（耳一片）（尤-hJ=麒兀-%）（兀一叫）一

（1）也■耳JX1~窃

+2（Fic也一日‘幻冷+上/Ax.）两妒+护）龙?

一2兀：

”（/F+屮）十2/护Jt一盒7咕'=0-—-

（2）

运算至此，弄式已经不龍再破化简*如前所述現在应将此式因式分解以此得到呜用一衣錢性关系・但这弁不間单，其中P（斗風隅梆風上的定直竊見橢测的方程，鳶咕这一关至在此艺也难

有用处，（若工心为具体敝宇应无毗问题［在此捞们提出一种睡幵貞杀因#分觀的方送。

讯察

（1）辛雅看出当戸点与川点或月点董合时⑴薦立即真-V^I.■心或刃弋”為■毗于是对干由⑴关系得来的⑵必然也在此时成立但这矗昔了尸点异于泌』两直的圣件因就为増根时的If眇而且此时霽足wg+mn"矗_%若将0）看为夭亍那的二次方程则由韦达定理可知正硝的覩为预=-琳宀-：

密-臥-gn"〔字一弘+彗単一片

=定点为（孚-珀与■-儿W“X也可招述対至元:

2.双曲线与抛物线

如图所示：

圆锥曲线（椭圆为图例）外有一定直线t,T为t上一动点过t作圆锥曲线的两条切线，连接切点形成圆锥曲线的弦称为T关于的圆锥曲线的切点弦，当T点在t上运动时切点弦也随之变化，但无论如何T点的切点弦必然过一定点。

这种问题乍一看会感到特别复杂，其实弄清楚了其中的原委后，更会让我们感受到圆锥曲线中蕴含几何性质的魅力！

（在解析圆锥曲线（下）中讲解）