全等三角形压轴题及其详解.docx

全等三角形压轴题及其详解.docx

《全等三角形压轴题及其详解.docx》由会员分享，可在线阅读，更多相关《全等三角形压轴题及其详解.docx（49页珍藏版）》请在冰豆网上搜索。

全等三角形压轴题及其详解

全等三角形压轴题

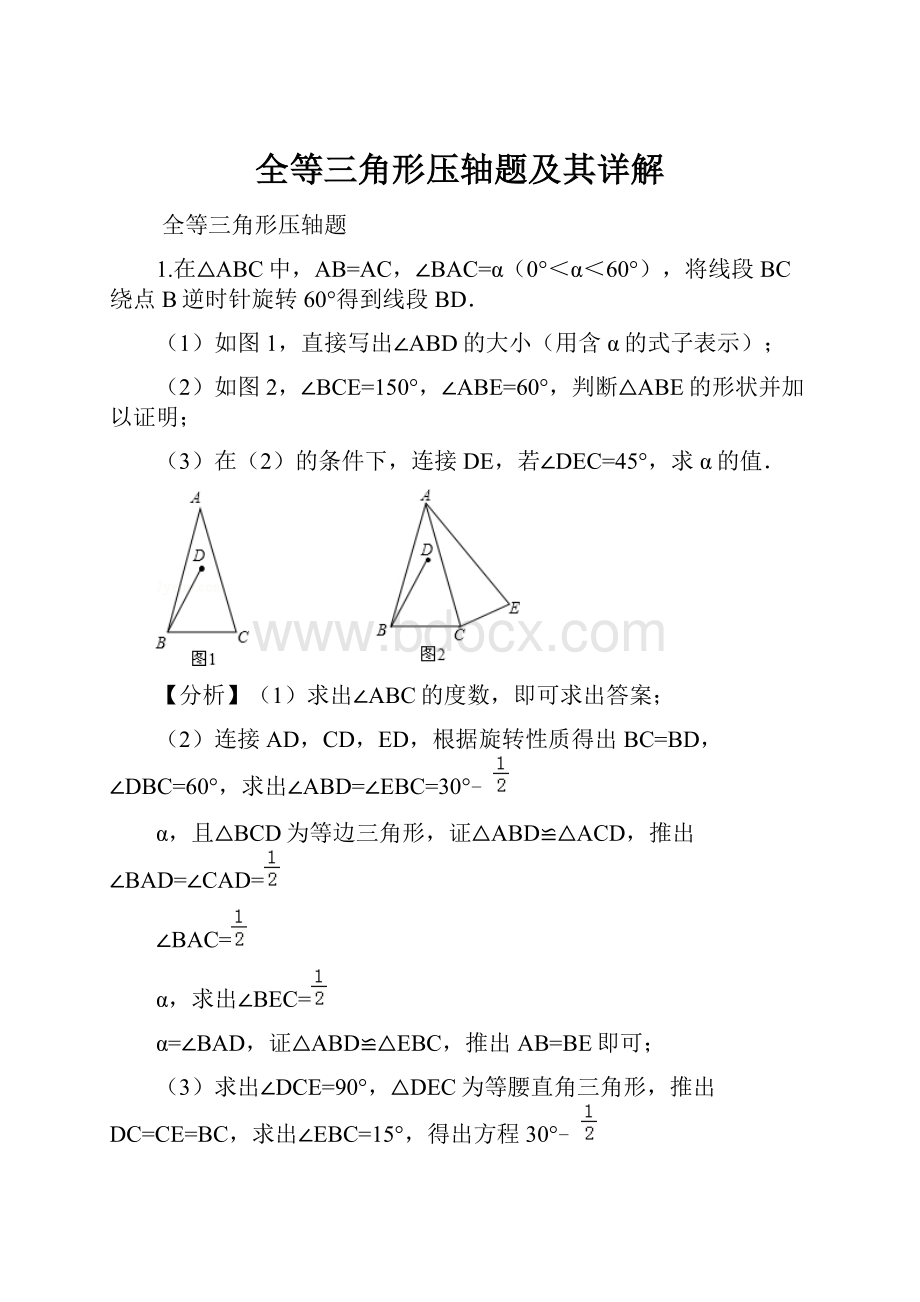
1.在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），将线段BC绕点B逆时针旋转60°得到线段BD．

（1）如图1，直接写出∠ABD的大小（用含α的式子表示）；

（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；

（3）在

（2）的条件下，连接DE，若∠DEC=45°，求α的值．

【分析】

（1）求出∠ABC的度数，即可求出答案；

（2）连接AD，CD，ED，根据旋转性质得出BC=BD，∠DBC=60°，求出∠ABD=∠EBC=30°﹣

α，且△BCD为等边三角形，证△ABD≌△ACD，推出∠BAD=∠CAD=

∠BAC=

α，求出∠BEC=

α=∠BAD，证△ABD≌△EBC，推出AB=BE即可；

（3）求出∠DCE=90°，△DEC为等腰直角三角形，推出DC=CE=BC，求出∠EBC=15°，得出方程30°﹣

α=15°，求出即可．

【解答】

（1）解：

∵AB=AC，∠A=α，

∴∠ABC=∠ACB=

（180°﹣∠A）=90°﹣

α，

∵∠ABD=∠ABC﹣∠DBC，∠DBC=60°，

即∠ABD=30°﹣

α；

（2）△ABE是等边三角形，

证明：

连接AD，CD，ED，

∵线段BC绕B逆时针旋转60°得到线段BD，

则BC=BD，∠DBC=60°，

∵∠ABE=60°，

∴∠ABD=60°﹣∠DBE=∠EBC=30°﹣

α，且△BCD为等边三角形，

在△ABD与△ACD中

∴△ABD≌△ACD（SSS），

∴∠BAD=∠CAD=

∠BAC=

α，

∵∠BCE=150°，

∴∠BEC=180°﹣（30°﹣

α）﹣150°=

α=∠BAD，

在△ABD和△EBC中

∴△ABD≌△EBC（AAS），

∴AB=BE，

∴△ABE是等边三角形；

（3）解：

∵∠BCD=60°，∠BCE=150°，

∴∠DCE=150°﹣60°=90°，

∵∠DEC=45°，

∴△DEC为等腰直角三角形，

∴DC=CE=BC，

∵∠BCE=150°，

∴∠EBC=

（180°﹣150°）=15°，

∵∠EBC=30°﹣

α=15°，

∴α=30°．

【点评】本题考查了全等三角形的性质和判定，等边三角形的性质和判定，等腰直角三角形的判定和性质的应用，注意：

全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的性质是全等三角形的对应边相等，对应角相等．

2.已知，Rt△ABC中，∠ACB=90°，∠CAB=30°．分别以AB、AC为边，向三角形外作等边△ABD和等边△ACE．

（1）如图1，连接线段BE、CD．求证：

BE=CD；

（2）如图2，连接DE交AB于点F．求证：

F为DE中点．

【解答】证明：

（1）∵△ABD和△ACE是等边三角形，

∴AB=AD，AC=AE，∠DAB=∠EAC=60°，

∴∠DAB+∠BAC=∠EAC+∠BAC，即∠DAC=∠BAE，

在△DAC和△BAE中，

，

∴△DAC≌△BAE（SAS），

∴DC=BE；

（2）如图，作DG∥AE，交AB于点G，

由∠EAC=60°，∠CAB=30°得：

∠FAE=∠EAC+∠CAB=90°，

∴∠DGF=∠FAE=90°，

又∵∠ACB=90°，∠CAB=30°，

∴∠ABC=60°，

又∵△ABD为等边三角形，∠DBG=60°，DB=AB，

∴∠DBG=∠ABC=60°，

在△DGB和△ACB中，

，

∴△DGB≌△ACB（AAS），

∴DG=AC，

又∵△AEC为等边三角形，∴AE=AC，

∴DG=AE，

在△DGF和△EAF中，

，

∴△DGF≌△EAF（AAS），

∴DF=EF，即F为DE中点．

3.在课外小组活动时，小慧拿来一道题（原问题）和小东、小明交流．

原问题：

如图1，已知△ABC，∠ACB=90°，∠ABC=45°，分别以AB、BC为边向外作△ABD与△BCE，且DA=DB，EB=EC，∠ADB=∠BEC=90°，连接DE交AB于点F．探究线段DF与EF的数量关系．

小慧同学的思路是：

过点D作DG⊥AB于G，构造全等三角形，通过推理使问题得解．

小东同学说：

我做过一道类似的题目，不同的是∠ABC=30°，∠ADB=∠BEC=60度．

小明同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况．

请你参考小慧同学的思路，探究并解决这三位同学提出的问题：

（1）写出原问题中DF与EF的数量关系；

（2）如图2，若∠ABC=30°，∠ADB=∠BEC=60°，原问题中的其他条件不变，你在

（1）中得到的结论是否发生变化？

请写出你的猜想并加以证明；

（3）如图3，若∠ADB=∠BEC=2∠ABC，原问题中的其他条件不变，你在

（1）中得到的结论是否发生变化？

请写出你的猜想并加以证明．

【分析】本题的解题思路是通过构建全等三角形来求解．先根据直角三角形的性质，等边三角形的性质得到一些隐含的条件，然后根据所得的条件来证明所构建的三角形的全等；再根据全等三角形的对应边相等得出DF=EF的猜想．

【解答】解：

（1）DF=EF．

（2）猜想：

DF=FE．

证明：

过点D作DG⊥AB于G，则∠DGB=90度．

∵DA=DB，∠ADB=60度．

∴AG=BG，△DBA是等边三角形．

∴DB=BA．

∵∠ACB=90°，∠ABC=30°，

∴AC=

AB=BG．

在Rt△DBG和Rt△BAC中

∴Rt△DBG≌Rt△BAC（HL）．

∴DG=BC．

∵BE=EC，∠BEC=60°，

∴△EBC是等边三角形．

∴BC=BE，∠CBE=60度．

∴DG=BE，∠ABE=∠ABC+∠CBE=90°．

∵∠DFG=∠EFB，∠DGF=∠EBF，

在△DFG和△EFB中

∴△DFG≌△EFB（AAS）．

∴DF=EF．

（3）猜想：

DF=FE．

证法一：

过点D作DH⊥AB于H，连接HC，HE，HE交CB于K，则∠DHB=90度．

∵DA=DB，

∴AH=BH，∠1=∠HDB．

∵∠ACB=90°，

∴HC=HB．

在△HBE和△HCE中

∴△HBE≌△HCE（SSS）．

∴∠2=∠3，∠4=∠BEH．

∴HK⊥BC．

∴∠BKE=90°．∴∠3+∠ABC=90°

∵∠ADB=∠BEC=2∠ABC，

∴∠HDB=∠BEH=∠ABC．

∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°，

∴∠3=∠DBH

∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°=∠DHB

又∵HB是公共边，所以△DBH≌△EHB

∴DH=BE

同理可以证明△DHF≌△EBF

∴DF=EF．

4.已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为E、F，Q为斜边AB的中点．

（1）如图1，当点P与点Q重合时，AE与BF的位置关系是　AE∥BF　，QE与QF的数量关系是　QE=QF　；

（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；

（3）如图3，当点P在线段BA（或AB）的延长线上时，此时

（2）中的结论是否成立？

请画出图形并给予证明．

【分析】

（1）根据AAS推出△AEQ≌△BFQ，推出AE=BF即可；

（2）延长EQ交BF于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可；

（3）延长EQ交FB于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可．

【解答】解：

（1）如图1，

当点P与点Q重合时，AE与BF的位置关系是AE∥BF，QE与QF的数量关系是AE=BF，

理由是：

∵Q为AB的中点，

∴AQ=BQ，

∵AE⊥CQ，BF⊥CQ，

∴AE∥BF，∠AEQ=∠BFQ=90°，

在△AEQ和△BFQ中

∴△AEQ≌△BFQ，

∴QE=QF，

故答案为：

AE∥BF，QE=QF；

（2）

QE=QF，

证明：

延长EQ交BF于D，

∵由

（1）知：

AE∥BF，

∴∠AEQ=∠BDQ，

在△AEQ和△BDQ中

∴△AEQ≌△BDQ，

∴EQ=DQ，

∵∠BFE=90°，

∴QE=QF；，

（3）当点P在线段BA（或AB）的延长线上时，此时

（2）中的结论成立，

证明：

延长EQ交FB于D，如图3，

∵由

（1）知：

AE∥BF，

∴∠AEQ=∠BDQ，

在△AEQ和△BDQ中

∴△AEQ≌△BDQ，

∴EQ=DQ，

∵∠BFE=90°，

∴QE=QF．

5.在△ABC中，AB=AC，∠BAC=60°，点E为直线AC上一点，D为直线BC上的一点，且DA=DE．

当点D在线段BC上时，如图①，易证：

BD+AB=AE；

当点D在线段CB的延长线上时，如图②、图③，猜想线段BD，AB和AE之间又有怎样的数量关系？

写出你的猜想，并选择一种情况给予证明．

【分析】图②中，论：

BD+AE=AB，作EM∥AB交BC于M，先证明△EMC是等边三角形得CE=CM，AE=BM，再证明△ABD≌△DEM，得DB=EM=MC由此可以对称结论．图③中，结论：

BD﹣AE=AB，证明方法类似．

【解答】解；如图②中，结论：

BD+AE=AB．

理由：

作EM∥AB交BC于M，

∵△ABC是等边三角形，

∴∠ABC=∠C=∠BAC=60°，AB=BC=AC，

∴∠CEM=∠CAB=60°，∠CME=∠CBA=60°，

∴△CME是等边三角形，

∴CE=CM=EM，∠EMC=60°，

∴AE=BM，

∵DA=DE，

∴∠DAE=∠DEA，

∴∠BAC+∠DAB=∠C+∠EDM，

∴∠DAB=∠EDM，

∵∠ABD=180°﹣∠ABC=120°，∠EMD=180°﹣∠EMC=120°，

∴∠ABD=∠DME，

在△ABD和△DEM中，

，

∴△ABD≌△DEM，

∴DB=EM=CM，

∴DB+AE=CM+BM=BC=AB．

如图③中，结论：

BD﹣AE=AB．

理由：

作EM∥AB交BC于M，

∵△ABC是等边三角形，

∴∠ABC=∠C=∠BAC=60°，AB=BC=AC，

∴∠CEM=∠CAB=60°，∠CME=∠CBA=60°，

∴△CME是等边三角形，

∴CE=CM=EM，∠EMC=∠MEC=60°，

∴AE=BM，

∵DA=DE，

∴∠DAE=∠DEA，

∴∠C+∠ADC=∠MEC+∠EDDEM，

∴∠ADB=∠DEM，

∵∠ABD=180°﹣∠ABC=120°，∠EMD=180°﹣∠EMC=120°，

∴∠ABD=∠DME，

在△ABD和△DEM中，

，

∴△ABD≌△DME，

∴DB=EM=CM，

∴DB﹣AE=CM﹣BM=BC=AB．

【点评】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解题的关键是添加辅助线构造全等三角形，注意形变证明方法基本不变，属于中考常考题型．

6.如图1，我们定义：

在四边形ABCD中，若AD=BC，且∠ADB+∠BCA=180°，则把四边形ABCD叫做互补等对边四边形．

（1）如图2，在等腰△ABE中，AE=BE，四边形ABCD是互补等对边四边形，求证：

∠ABD=∠BAC=

∠AEB．

（2）如图3，在非等腰△ABE中，若四边形ABCD仍是互补等对边四边形，试问∠ABD=∠BAC=

∠AEB是否仍然成立？

若成立，请加以证明；若不成立，请说明理由．

【分析】

（1）根据等边对等角可得∠EAB=∠EBA，根据四边形ABCD是互补等对边四边形，可得AD=BC，根据SAS可证△ABD≌△BAC，根据全等三角形的性质可得∠ABD=∠BAC，再根据等腰三角形的性质即可证明；

（2）仍然成立；理由如下：

如图所示：

过点A、B分别作BD的延长线与AC的垂线，垂足分别为G、F，证明△AGD≌△BFC，得到AG=BF，又AB=BA，所以△ABC≌△BAF，得到∠ABD=∠BAC，根据∠ADB+∠BCA=180°，得到∠EDB+∠ECA=180°，进而得到∠AEB+∠DHC=180°，由∠DHC+∠BHC=180°，所以∠AEB=∠BHC．因为∠BHC=∠BAC+∠ABD，∠ABD=∠BAC，所以∠ABD=∠BAC=

∠AEB．

【解答】解：

（1）∵AE=BE，

∴∠EAB=∠EBA，

∵四边形ABCD是互补等对边四边形，

∴AD=BC，

在△ABD和△BAC中，

，

∴△ABD≌△BAC（SAS），

∴∠ADB=∠BCA，

又∵∠ADB+∠BCA=180°，

∴∠ADB=∠BCA=90°，

在△ABE中，∵∠EAB=∠EBA=

=90°﹣

∠AEB，

∴∠ABD=90°﹣∠EAB=90°﹣（90°﹣

∠AEB）=

∠AEB，

同理：

∠BAC=

∠AEB，

∴∠ABD=∠BAC=

∠AEB；

（2）仍然成立；

理由如下：

如图③所示：

过点A、B分别作BD的延长线与AC的垂线，垂足分别为G、F，

∵四边形ABCD是互补等对边四边形，

∴AD=BC，∠ADB+∠BCA=180°，

又∠ADB+ADG=180°，

∴∠BCA=∠ADC，

又∵AG⊥BD，BF⊥AC，

∴∠AGD=∠BFC=90°，

在△AGD和△BFC中，

∴△AGD≌△BFC，

∴AG=BF，

在△ABG和△BAF中，

∴△ABG≌△BAF，

∴∠ABD=∠BAC，

∵∠ADB+∠BCA=180°，

∴∠EDB+∠ECA=180°，

∴∠AEB+∠DHC=180°，

∵∠DHC+∠BHC=180°，

∴∠AEB=∠BHC．

∵∠BHC=∠BAC+∠ABD，∠ABD=∠BAC，

∴∠ABD=∠BAC=

∠AEB．

【点评】本题考查了等腰三角形的性质、全等三角形的判定与性质，解决本题的关键是根据SAS证明△ABD≌△BAC．

7.已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作等边△ADE（顶点A、D、E按逆时针方向排列），连接CE．

（1）如图1，当点D在边BC上时，求证：

①BD=CE，②AC=CE+CD；

（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CE+CD是否成立？

若不成立，请写出AC、CE、CD之间存在的数量关系，并说明理由；

（3）如图3，当点D在边BC的反向延长线上且其他条件不变时，补全图形，并直接写出AC、CE、CD之间存在的数量关系．

【分析】

（1）根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE，从而得出结论；

（2）根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE，就可以得出BD=CE，就可以得出AC=CE﹣CD；

（3）先根据条件画出图形，根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE，就可以得出BD=CE，就可以得出AC=CD﹣CE．

【解答】解：

（1）∵△ABC和△ADE都是等边三角形，

∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°．

∴∠BAC﹣∠CAD=∠DAE﹣∠CAD，即∠BAD=∠CAE．

在△ABD和△ACE中，

，

∴△ABD≌△ACE（SAS），

∴BD=CE．

∵BC=BD+CD，AC=BC，

∴AC=CE+CD；

（2）AC=CE+CD不成立，

AC、CE、CD之间存在的数量关系是：

AC=CE﹣CD．

理由：

∵△ABC和△ADE都是等边三角形，

∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°．

∴∠BAC+∠CAD=∠DAE+∠CAD，

∴∠BAD=∠CAE

在△ABD和△ACE中，

∴△ABD≌△ACE（SAS）

∴BD=CE

∴CE﹣CD=BD﹣CD=BC=AC，

∴AC=CE﹣CD；

（3）补全图形（如图）

AC、CE、CD之间存在的数量关系是：

AC=CD﹣CE．

理由：

∵△ABC和△ADE都是等边三角形，

∴AB=AC=BC，AD=AE，∠BAC=∠DAE=60°．

∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，

∴∠BAD=∠CAE

在△ABD和△ACE中，

∴△ABD≌△ACE（SAS）

∴BD=CE．

∵BC=CD﹣BD，

∴BC=CD﹣CE，

∴AC=CD﹣CE．

【点评】本题考查了等边三角形的性质的运用，等式的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．

8.如图，已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE．G、F分别是DC与BE的中点．

（1）求证：

DC=BE；

（2）当∠DAB=80°，求∠AFG的度数；

（3）若∠DAB=α，则∠AFG与α的数量关系是　　．

【分析】

（1）根据等式的性质就可以得出∠DAC=∠BAE．就可以得出△ADC≌△ABE就可以得出DC=BE；

（2）连接AG，根据条件就可以得出△ADG≌△ABF，就可以求出AG=AF，∠GAF=∠DAB，由等腰三角形的性质就可以求出∠AFG的值，

（3）连接AG，根据条件就可以得出△ADG≌△ABF，就可以求出AG=AF，∠GAF=∠DAB，由等腰三角形的性质就可以表示∠AFG与a的关系．

【解答】解：

（1）∵∠DAB=∠CAE，

∴∠DAB+∠BAC=∠CAE+∠BAC，

∴∠DAC=∠BAE．

在△ADC和△ABE中

，

∴△ADC≌△ABE（SAS），

∴DC=BE；

（2）连接AG．

∵△ADC≌△ABE，

∴∠ADC=∠ABE．AD=AB．

∵G、F分别是DC与BE的中点，

∴DG=

DC，BF=

BE，

∴DG=BF．

在△ADG和△ABF中

，

∴△ADG≌△ABF（SAS），

∴AG=AF，∠DAG=∠BAF，

∴∠AGF=∠AFG，∠DAG﹣∠BAG=∠BAF﹣∠BAG，

∴∠DAB=∠GAF．

∵∠DAB=80°，

∴∠GAF=80°．

∵∠GAF+∠AFG+∠AGF=180°，

∴∠AFG=50°．

答：

∠AFG=50°；

（3）∵∠DAB=α，

∴∠GAF=α．

∵∠GAF+∠AFG+∠AGF=180°，

∴α+2∠AFG=180°，

∴∠AFG=90°﹣

α．

故答案为：

∠AFG=50°，90°﹣

α．

【点评】本题考查了全等三角形的判定及性质的运用，等式的性质的运用，等腰三角形的性质的运用，三角形内角和定理的运用，解答时证明三角形全等是关键．

9.△ABC是等边三角形，点D、E分别在边AB、BC上，CD、AE交于点F，∠AFD=60°．

（1）如图1，求证：

BD=CE；

（2）如图2，FG为△AFC的角平分线，点H在FG的延长线上，HG=CD，连接HA、HC，求证：

∠AHC=60°；

（3）在

（2）的条件下，若AD=2BD，FH=9，求AF长．

【分析】

（1）根据等边三角形的性质得出AB=BC，∠BAC=∠C=∠ABE=60°，根据SAS推出△ABE≌△BCD，即可证得结论；

（2）根据角平分线的性质定理证得CM=CN，利用∠CEM=∠ACE+∠CAE=60°+∠CAE，∠CGN=∠AFH+∠CAE=60°+∠CAE，得出∠CEM=∠CGN，然后根据AAS证得△ECM≌△GCN，得出CG=CE，EM=GN，∠ECM=∠GCN，进而证得△AMC≌△HNC，得出∠ACM=∠HCN，AC=HC，从而证得△ACH是等边三角形，证得∠AHC=60°；

（3）在FH上截取FK=FC，得出△FCK是等边三角形，进一步得出FC=KC=FK，∠ACF=∠HCK，证得△AFC≌△HKC得出AF=HK，从而得到HF=AF+FC=9，由AD=2BD可知AG=2CG，再由

=

，根据等高三角形面积比等于底的比得出

=

=

=2，再由AF+FC=9求得．

【解答】解：

（1）如图1，∵△ABC是等边三角形，

∴∠B=∠ACE=60°BC=AC，

∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°，

∴∠BCD=∠CAE，

在△ABE和△BCD中，

∴△ABE≌△BCD（ASA），

∴BD=CE；

（2）如图2，作CM⊥AE交AE的延长线于M，作CN⊥HF于N，

∵∠EFC=∠AFD=60°

∴∠AFC=120°，

∵FG为△AFC的角平分线，

∴∠CFH=∠AFH=60°，

∴∠CFH=∠CFE=60°，

∵CM⊥AE，CN⊥HF，

∴CM=CN，

∵∠CEM=∠ACE+∠CAE=60°+∠CAE，∠CGN=∠AFH+∠CAE=60°+∠CAE，

∴∠CEM=∠CGN，

在△ECM和△GCN中

∴△ECM≌△GCN（AAS），

∴CE=CG，EM=GN，∠ECM=∠GCN，

∴∠MCN=∠ECG=60°，

∵△ABE≌△BCD，

∵AE=CD，

∵HG=CD，

∴AE=HG，

∴AE+EM=HG+GN，即AM=HN，

在△AMC和△HNC中

∴△AMC≌△HNC（SAS），

∴∠ACM=∠HCN，AC=HC，

∴∠ACM﹣∠ECM=∠HCN﹣∠GCN，即∠ACE=∠HCG=60°，

∴△ACH是等边三角形，

∴∠AHC=60°；

（3）如图3，在FH上截取FK=FC，

∵∠HFC=60°，

∴△FCK是等边三角形，

∴∠FKC=60°，FC=KC=FK，

∵∠ACH=60°，

∴∠ACF=∠HCK，

在△AFC和△HKC中

∴△AFC≌△HKC（SAS），

∴AF=HK，

∴HF=AF+FC=9，

∵AD=2BD，BD=CE=CG，AB=AC，

∴AG=2CG，

∴

=

=

，

作GW⊥AE于W，GQ⊥DC于Q，

∵FG为△AFC的角平分线，

∴GW=GQ，

∵

=

=

=

，

∴AF=2CF，

∴AF=6．

【点评】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，角平分线的性质，找出辅助线根据全等三角形和等边三角形是解题的关键．

10.如图1，△ABE是等腰三角形，AB=AE，∠BAE=45°，过点B作BC⊥AE于点C，在BC上截取CD=CE，连接AD、DE并延长AD交BE于点P；

（1）求证：

AD=BE；

（2）试说明AD平分∠BAE；

（3）如图2，将△CDE绕着点C旋转一定的角度，那么AD与BE的位置关系是否发生变化，说明理由．

【分析】

（1）利用SAS证明△BCE≌△ACD，根据全等三角形的对应边相等得到AD=BE．

（2）根据△BCE≌△ACD，得到∠EBC=∠DAC，由∠BDP=∠ADC，得到∠BPD=∠DCA=90°，利用等腰三角形的三线合一，即可得到AD平分∠BAE；

（3）AD⊥BE不发生变化．由△BCE≌△ACD，得到∠EBC=∠DAC，由对顶角相等得到∠BFP=∠ACF，根据三角形内角和为180°，所以∠BPF=∠ACF=90°，即AD⊥BE．

【解答】解：

（1）∵BC⊥AE，∠BAE=45°，

∴∠CBA=∠CAB，

∴BC=CA，

在△BCE和△ACD中，

∴△BCE≌△ACD，

∴AD=BE．